👀作者简介：大家好，我是 快到碗里来~
🚩🚩 个人主页：快到碗里来~
支持我：点赞+关注~不迷路🧡🧡🧡
✔系列专栏：数据结构与算法⚡⚡⚡
(❁´◡`❁)励志格言：在我有生之日，做一个真诚的人，不放弃对生活的热爱和执着，在有限的时空里，过无限广大的日子。（by 三毛）🤞🤞
知识导航
- 一.图的基本实现前导算法
- 1.代码结构设计
- 2.添加节点（addVertex）
- 3.添加边（addEdge）
- 4.删除节点（removeVertex）
- 5.删除边（removeEdge）
- 二、图的遍历
- 1.bfs算法
- 2.dfs算法
- （1）递归实现
- （2）非递归实现
- 3.leetcode精选例题
- 三.最小生成树
- 1.普利姆（prim）算法
- 2.克鲁斯尔(kruskal)算法
- 四.最短路径
- （1）最短路径之无权图
- （2）最短路径之负权环
- 算法实现
- 1 .Dijkstra（迪杰斯特拉算法）
- 算法思想具体形象化（缓慢拉绳子案例）
- 2. Bellman-Ford（贝尔曼-福特算法）
- 五.拓扑排序
- 1.AOV网（Activity On Vertex Network）
- 2.拓扑排序原理
一.图的基本实现前导算法
1.代码结构设计
上节基础篇篇我们提到了图的两种实现方法–>临接矩阵实现法以及邻接表实现法。并分析了他们各自的利弊。
所以为了权衡他们的利弊，我们尝试用一种介于邻接矩阵和邻接表之间实现的方法，但从实现形式上他更偏向于邻接表的一种方法。😎😎
1.在图的实现类中定义一个哈希表和哈希集合分别存储图中所有的点和边。
//将节点的值和节点联系起来,(存放所有的节点)
private final Map<V ,Vertex<V,E>> vertexes =new HashMap<>();
//edges存放所有的边，为什么用集合因为inEdges和outEdges有重复避免出现重复节点
private final Set<Edge<V,E>> edges=new HashSet<>();
2.实现节点类（注意在节点类中我们有定义了两个集合分别存储节点的出度和入度的边兼容了无向图和有向图）
在节点类中重写了equals()和hashCode()方法使他具备可以比较的条件
//V自身顶点的类型，E顶点上权值的类型
private static class Vertex<V,E>{
public Vertex(V val) {
this.val = val;
}
V val;
//分别存放入，出节点的边
//节点的出入线不考虑顺序所以用Set更合适
Set<Edge<V,E>> inEdges=new HashSet<>();
Set<Edge<V,E>> outEdges=new HashSet<>();
//边的比较是基于节点的所以节点也要重写equals()和hashcode()
//val值相等就认为两个节点相等
@Override
public boolean equals(Object obj) {
return Objects.equals(val,((Vertex<V,E>)obj).val);
}
@Override
public int hashCode() {
return val==null?0:val.hashCode();
}
@Override
public String toString() {
return val== null ? "null" : val.toString();
}
}
3.实现边（Edge类）
这里重写了equals()方法,只要一条边的起始节点和终止节点相等我们就认为这两条边相等。 toInfo（）方法实现了Edge类和EdgeInfo之间的转换，EdgeInfo是自定义存储边的信息的接口->是返回给外界的公共接口。
//V边所连节点的类型，E边上的权值
private static class Edge<V,E> {
public Edge(Vertex<V, E> from, Vertex<V, E> to) {
this.from = from;
this.to = to;
}
//该线的尾部
Vertex<V,E> from;
//该线指向的节点
Vertex<V,E> to;
E weight;
@Override
public boolean equals(Object obj) {
//判断边的相等归根结底是判断节点的相等
Edge<V,E> edge=(Edge<V,E>)obj;
return Objects.equals(edge.from,from)&&Objects.equals(edge.to,to);
}
@Override
public int hashCode() {
//自己定义哈希表的规则，这里写31是借鉴字符串的哈希值的转换规则，是哈希表更加均匀
return from.hashCode()*31+to.hashCode();
}
@Override
public String toString() {
return "Edge{" +
"from=" + from +
", to=" + to +
", weight=" + weight +
'}';
}
//Edge与EdgeInfo之间的比较
public EdgeInfo<V,E> toInfo(){
//Cannot infer arguments 错误分析：检查泛型的类型对应
return new EdgeInfo<>(from.val,to.val,weight);
}
}
4.公共方法和接口抽调为抽象类
package grapth;
import java.util.LinkedList;
import java.util.List;
import java.util.Map;
import java.util.Set;
abstract public class Graph<V,E> {
public Graph(){}
//权值比较
//自定义比较方法传入
protected WeightManager<E> weightManager;
public Graph(WeightManager<E> e){
this.weightManager=e;
}
public abstract int edgesSize();
public abstract int verticesSize();
public abstract void addVertex(V v);
public abstract void addEdge(V from, V to);
public abstract void addEdge(V from, V to, E weight);
public abstract void removeVertex(V v);
public abstract void removeEdge(V from, V to);
//广度遍历
//传入控制访问器
public abstract void bfs(V begin,VertexVisitor<V>visitor);
public abstract void dfs(V begin,VertexVisitor<V>visitor);
public abstract void dfs2(V begin,VertexVisitor<V>visitor);
//返回拓扑序列（打印顺序）
public abstract List<V> topologicalSort();
public abstract Set<EdgeInfo<V,E>> mst();
public abstract Map<V,pathInfo<V,E>> shortedPath(V v);
//路径信息
public static class pathInfo<V,E>{
protected E weight;//存放路径权值之和
protected List<EdgeInfo<V,E>> edgeInfos=new LinkedList<>();//存放路径边的信息
public void setWeight(E weight) {
this.weight = weight;
}
public E getWeight(){
return weight;
}
public List<EdgeInfo<V, E>> getEdgeInfos() {
return edgeInfos;
}
public void setEdgeInfos(List<EdgeInfo<V, E>> edgeInfos) {
this.edgeInfos = edgeInfos;
}
public pathInfo(){}
@Override
public String toString() {
return "pathInfo{" +
"weight=" + weight +
", edgeInfos=" + edgeInfos +
'}';
}
}
public interface WeightManager<E>{
int compare(E e1, E e2);
E add(E e1,E e2);
E zero();
}
public static class EdgeInfo<V,E>{
V from;
V to;
E weight;
public EdgeInfo(){}
public EdgeInfo(V from, V to, E weight) {
this.from = from;
this.to = to;
this.weight = weight;
}
@Override
public String toString() {
return "EdgeInfo{" +
"from=" + from +
", to=" + to +
", weight=" + weight +
'}';
}
}
interface VertexVisitor<V>{
boolean visit(V v);
}
}
2.添加节点（addVertex）
在添加节点中先前建立的储存所有节点的哈希表就派上用场了，如果表中本来就存在这个节点就没有必有二次添加，因为哈希表是不会自动去重的
@Override
public void addVertex(V v) {
if(vertexes.containsKey(v)){
return;
}
vertexes.put(v,new Vertex<>(v));
}
3.添加边（addEdge）
在添加边过程中要考虑到边的起始节点在图中是否一开始就存在，如果两个节点本身就存在则只需链接成边，如果有权值的话更新权值即可
如果两个节点本身不存在则需要重新创建节点。最后不管哪种情况都需要重新更新节点的入度出度信息。
//服务于无向图
@Override
public void addEdge(V from, V to) {
//有向图去掉权值就是无项图的边
addEdge(from,to,null);
}
//服务于无向图
@Override
public void addEdge(V from, V to, E weight) {
//先保证两个value的节点都存在
Vertex<V,E> fromVertex=vertexes.get(from);
if(fromVertex==null)
{
fromVertex=new Vertex<>(from);
vertexes.put(from,fromVertex);
}
Vertex<V,E> toVertex=vertexes.get(to);
if(toVertex==null)
{
toVertex=new Vertex<V,E>(to);
vertexes.put(to,toVertex);
}
//保证顶点一定存在了
Edge<V,E> edge=new Edge<V,E>(fromVertex,toVertex);
edge.weight=weight;
/**
* 问：edges是创建的节点怎么回在集合中找到？
* 这就是重写equals的意义了，这里在比较的时候不是比较的内存地址，是比较的起始地址是否相等
*
*/
//这里的contains底层时调用了equals()方法，所以要重写比较规则和哈希值
//如果这里能够删除就代表起始点之间已经存在边了，这里需要更新的就是权值
if(fromVertex.outEdges.remove(edge)){
//返回boolean值,为true这个点一定存在
//toEdges和outEdges是同一个线都将其删除
toVertex.inEdges.remove(edge);
edges.remove(edge);
}
//将带有最新权值的边加入（一删一添加的过程中其实是更新了权值）
fromVertex.outEdges.add(edge);
toVertex.inEdges.add(edge);
edges.add(edge);
}
4.删除节点（removeVertex）
这里需要注意的是在删除节点过程中，这个节点的入度和出度的边都会删除，与出度，入度的边对应的edge.to（边的终点的边）的入度也需要更新。
在一边遍历一边删除过程中肯定会出现问题（注意一边遍历一边删除大概率会出现问题）所以在进行一边遍历一边删除的操作，一般用迭代器进行执行。
@Override
public void removeVertex(V v) {
//删除并返回value
Vertex<V,E> vertex=vertexes.remove(v);
if(vertex==null)return;
/*边遍历边删除从逻辑上向很有可能出现问题，java中一边遍历一边删除要用迭代器
vertex.outEdges.forEach(( Edge<V,E>edge)->{
//删除边就是删除两端的节点
removeEdge(edge.from.val,edge.to.val);
});*/
/*
1.Iterator<Edge<V,E>> iterator=vertex.outEdges.iterator()
.iterator()告诉迭代器接收vertex.outEdges，接收类型为Edge
2.iterator.hasNext()类似于for循环遍历outEdges
*/
//一边遍历一边删除用迭代器
for(Iterator<Edge<V,E>> iterator=vertex.outEdges.iterator();iterator.hasNext();){
//获得遍历中的边
Edge<V,E> edge=iterator.next();
//删除该边指向节点的入度操作不受影响，因为遍历的是outEdges.iterator()
edge.to.inEdges.remove(edge);
edges.remove(edge);
//删除outEdges，因为受到边遍历边删除的影响所以讲它交给迭代器进行删除（这个方法会帮你做好一切）
iterator.remove();
}
for(Iterator<Edge<V,E>> iterator=vertex.inEdges.iterator();iterator.hasNext();){
//获得遍历中的边
Edge<V,E> edge=iterator.next();
//删除outEdges，因为受到边遍历边删除的影响所以讲它交给迭代器进行删除（这个方法会帮你做好一切）
iterator.remove();
//删除该边指向节点的入度操作不受影响，因为遍历的是outEdges.iterator()
edge.from.outEdges.remove(edge);
edges.remove(edge);
}
}
5.删除边（removeEdge）
@Override
public void removeEdge(V from, V to) {
//返回值是from的节点
Vertex<V,E> fromVertex=vertexes.get(from);
if(fromVertex==null)return;
Vertex<V,E> toVertex=vertexes.get(to);
if(toVertex==null)return;
//确定这个边已经存在了
//新创建的边怎么会找到？判定两个边相等只是看起始点是不是相同
Edge<V,E> edge=new Edge<V,E>(fromVertex,toVertex);
if(fromVertex.outEdges.remove(edge)){
//返回boolean值,为true这个点一定存在
//toEdges和outEdges是同一个线都将其删除
toVertex.inEdges.remove(edge);
edges.remove(edge);
}
}
二、图的遍历
◼ 图的遍历
从图中某一顶点出发访问图中其余顶点，且每一个顶点仅被访问一次
◼ 图有2种常见的遍历方式（有向图、无向图都适用）
广度优先搜索（Breadth First Search，BFS），又称为宽度优先搜索、横向优先搜索
深度优先搜索（Depth First Search，DFS）
✓ 发明“深度优先搜索”算法的2位科学家在1986年共同获得计算机领域的最高奖：图灵奖
1.bfs算法
bfs算法本质山和二叉树的层序遍历是一种方式，二叉树本质上也属于图的范畴。
🔥🔥bfs算法也是按照图的每一层进行遍历，那么图是如何区分第几层的呢？
答：根据每层节点的出度相连的节点（也就是说根据每一层节点的出度相连的节点化作下一层）
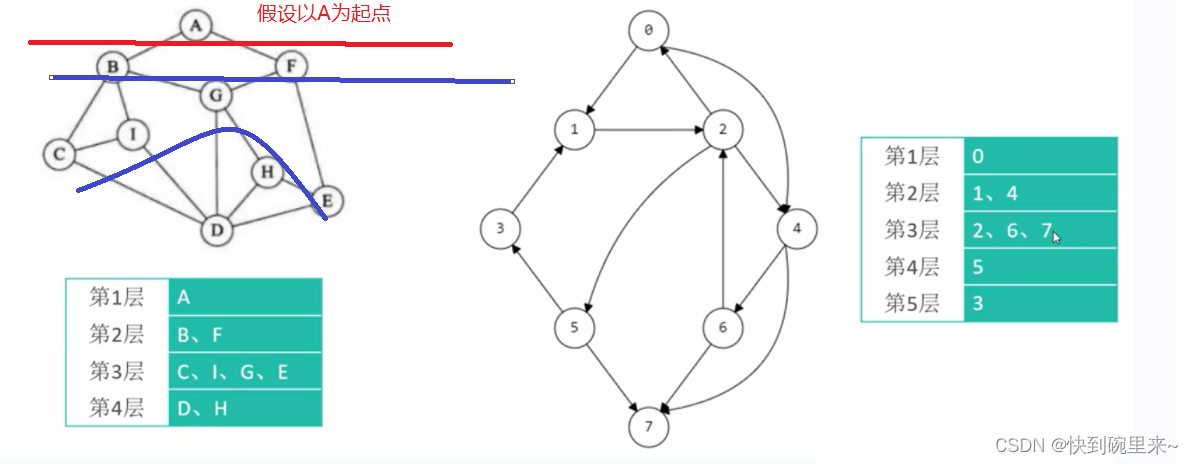上面在节点类（Vertex）的设计中我们了解到每个节点都有两个集合outEdges 和 inEdges分别存储出度的边和入度的边，所以我们只要顺着起始节点遍历outEdges
集合拿到出度的边,再由出度的边就可以拿到下一层节点（edge.to）.
注意：再进行每个节点outEdges的遍历的过程中，对于无向图肯定会有边产生重复遍历。所以要定义一个visited集合存放已经遍历过的边。
再实现过程中我们同样借助队列实现每有一个节点出队就进行遍历outEdges操作。
@Override
public void bfs(V begin,VertexVisitor<V> visitor) {
//begin从哪一个节点开始遍历
Vertex<V,E> vertex=vertexes.get(begin);
if(vertex==null)return;
//创建标记集合（c是创建标记数组）
//visited存储已经访问过的的节点
Set<Vertex<V,E>> visited=new HashSet<>();
Queue<Vertex<V,E>> queue=new LinkedList<>();
queue.offer(vertex);
while(!queue.isEmpty()){
Vertex<V,E> ver=queue.poll();
if(visitor.visit(ver.val))return;
//已经被访问的节点
visited.add(ver);
//拉姆达表达式的形式遍历（和for循环一个意思）
vertex.outEdges.forEach((Edge<V,E> edge)->{
if(!visited.contains(edge.to))
{
queue.add (edge.to);
visited.add(edge.to);
}
});
}
}
2.dfs算法
（1）递归实现
深度遍历类似于二叉树的前序遍历都可以用递归实现
@Override
public void dfs(V begin,VertexVisitor<V> visitor) {
Vertex<V,E> vertex=vertexes.get(begin);
if(begin==null)return;
dfs(vertex,new HashSet<>(),visitor);
}
private void dfs(Vertex<V,E> vertex,Set<Vertex<V,E>> visited,VertexVisitor<V> visitor){
if(visitor.visit(vertex.val))return;
//为了避免重复调用已经访问过的节点
visited.add(vertex);
for (Edge<V,E> edge:vertex.outEdges
) {
//已经访问过的节点不要访问第二遍
if(visited.contains(edge.to))continue;
dfs(edge.to,visited,visitor);
}
}
（2）非递归实现
再二叉树的学习过程中，我们直到递归的底层是由栈实现的。所以利用栈的相关操作可以替代栈操作。
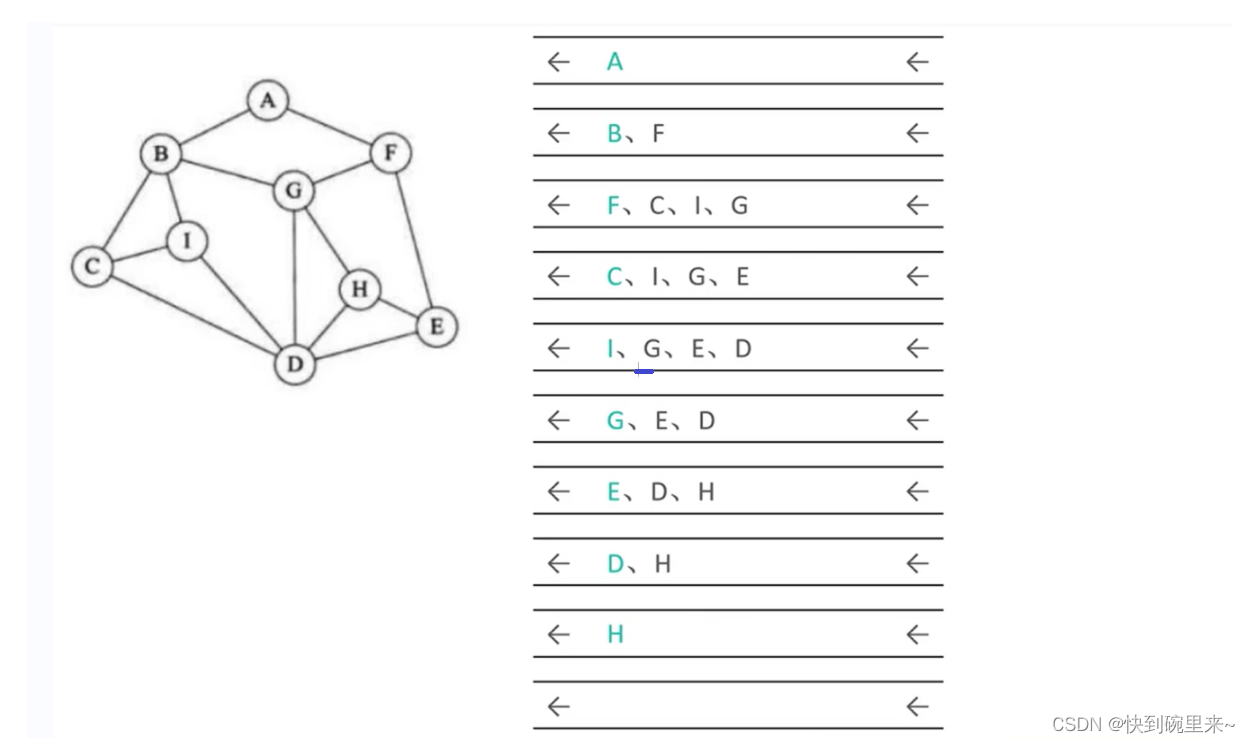
我们每遍历到一个节点就遍历他的出度的边，然后将edge.to节点和当前节点一起加入到栈中（为什么要把当前节点也加入到栈中？因为在遍历outEdges集合时我们是按照一条路径一直遍历到底的，当一条路径遍历到完后，还需要遍历该节点的其他路径）
假设以 1 为起点
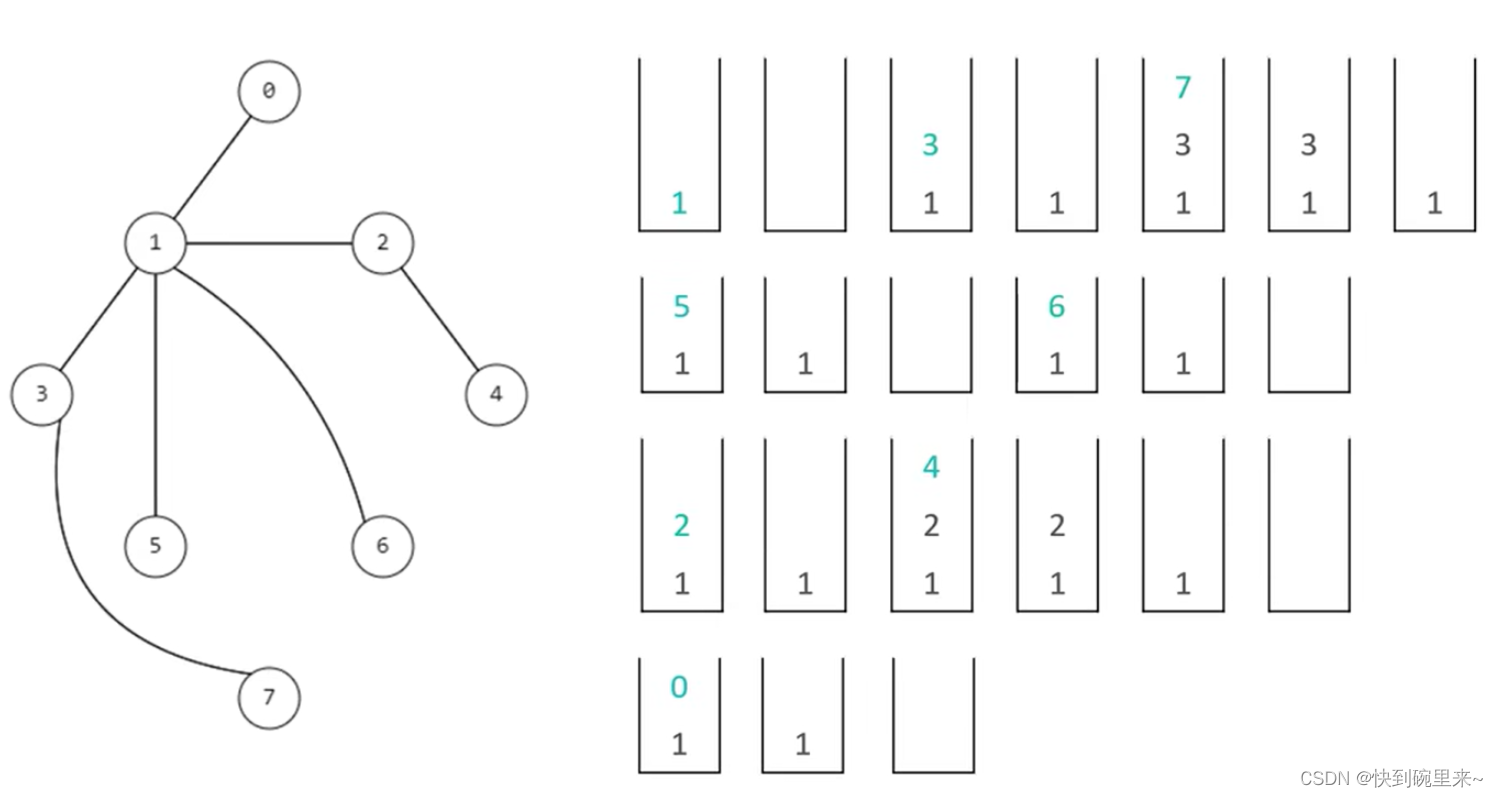注意在遍历中过也要建立标记集合，用来存储已经访问过的节点。用来防止路径重复访问。
@Override
public void dfs2(V begin,VertexVisitor<V> visitor) {
Vertex<V,E> beginVertex=vertexes.get(begin);
if(begin==null)return;
//标记数组
Set<Vertex<V,E>> visited =new HashSet<>();
Stack<Vertex<V,E>> stack=new Stack<>();
stack.push( beginVertex);
//先访问了起点
if(visitor .visit(beginVertex.val))return;
visited.add( beginVertex);
while(!stack.isEmpty()) {
Vertex<V, E> vertex1 = stack.pop();
for (Edge<V, E> edge : vertex1.outEdges) {
if (visited.contains(edge.to)) continue;
stack.push(edge.from);
stack.push(edge.to);
visited.add(edge.to);
if (visitor.visit(edge.to.val)) return;
break;
}
}
}
3.leetcode精选例题
- 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。
示例 1：
输入：digits = “23”
输出：[“ad”,“ae”,“af”,“bd”,“be”,“bf”,“cd”,“ce”,“cf”]
示例 2：
输入：digits = “”
输出：[]
示例 3：
输入：digits = “2”
输出：[“a”,“b”,“c”]
解题思路
对于2-9的电话号码我们很容易想到映射，将数字和字母对应起来。
形成映射的方法常见的有
1.利用java自带的HashMap形成映射。
2.利用二维数组形成映射。
对于解题思想我们可以将它假想成一颗号码树。(以实例一为例)
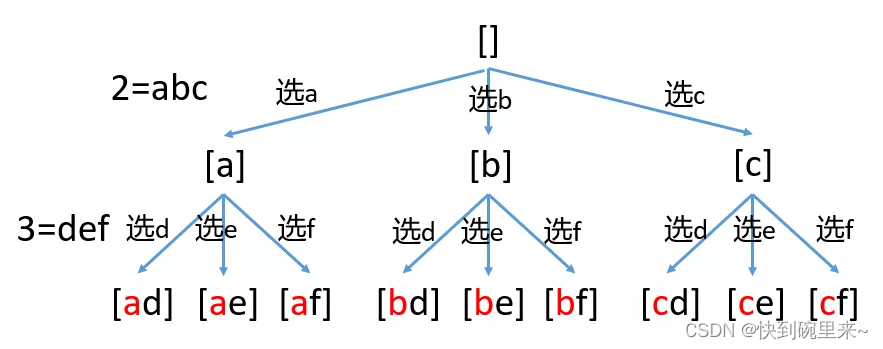
class Solution {
public List<String> letterCombinations(String digits) {
LinkedList<String> res=new LinkedList<>();
if(digits.length()==0||digits==null)return res;
char[] []tab={
{'a','b','c'},{'d','e','f'},{'g','h','i'},{'j','k','l'},{'m','n','o'},{'p','q','r','s'},{'t','u','v'},{'w','x','y','z'}
};
res.add("");//点睛之笔
while(res.peek().length()!=digits.length()){
String s=res.poll();
char [] str=tab[digits.charAt(s.length())-'2'];
for(int i=0;i<str.length;i++){
res.add(s+str[i]);
}
}
return res;
}
}
三.最小生成树
上节课我们提到连通图的概念---->（无向图任意两个顶点有相互连通的路径）。
🥳🥳这节我们引入生成树的概念。
1.生成树也被称为支撑树
2.连通图的极小连通子图拥有连通图的所有的n个节点，恰好有n-1条边。
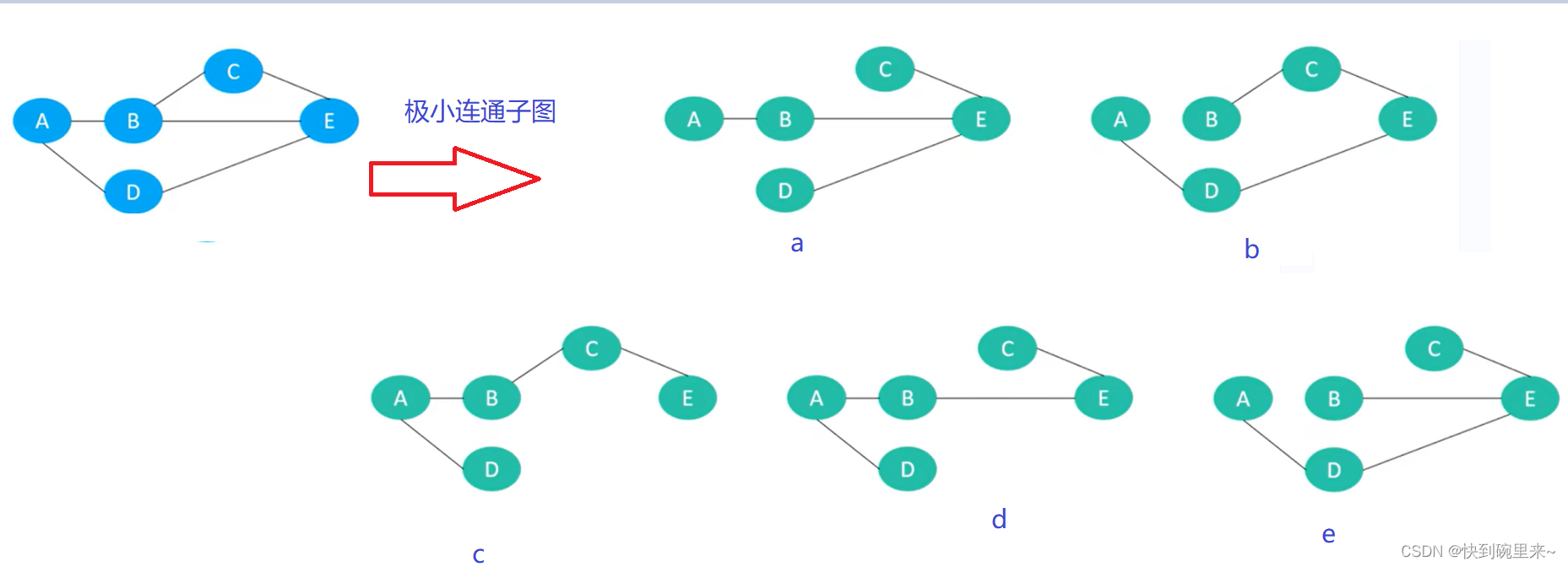
最小生成树
◼ 最小生成树（Minimum Spanning Tree，简称MST）
◼也称为最小权重生成树（Minimum Weight Spanning Tree）、最小支撑树
◼是所有生成树中，总权值最小的那棵(权值是之和是唯一的)
◼适用于有权的连通图（无向）
问：图的最小生成树是否是唯一的？
答：如果各个边的权值都是唯一的，那么最小生成树是唯一的
如果各个边的权值是相等的或者出现权值相等的边则最小生成树可能是不唯一的。
最小生成树的应用
最小生成树在许多领域都有重要的作用，例如
◼要在 n 个城市之间铺设光缆，使它们都可以通信
◼铺设光缆的费用很高，且各个城市之间因为距离不同等因素，铺设光缆的费用也不同
◼如何使铺设光缆的总费用最低？
实现最小生成树的主要通过普利姆算法和克鲁斯尔算法实现，在进行算法分析的前提我们先引入一个简单的定理–>切分定理
切分定理
◼ 切分（Cut）：把图中的节点分为两部分，称为一个切分
◼ 下图有个切分 C = (S, T)，S = {A, B, D}，T = {C, E}
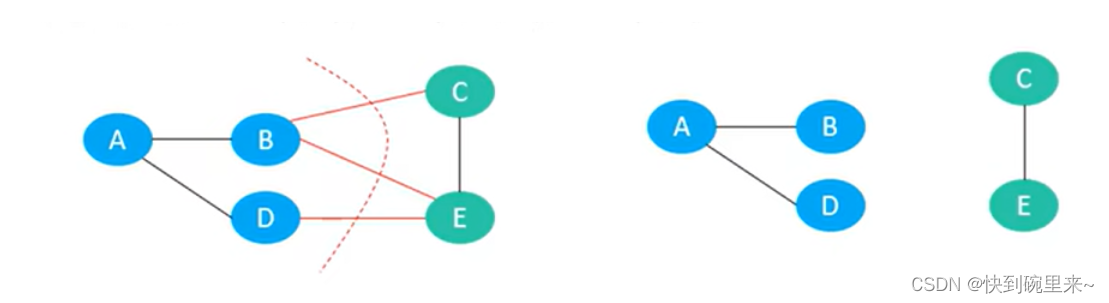
◼ 横切边（Crossing Edge）：如果一个边的两个顶点，分别属于切分的两部分，这个边称为横切边
◼ 比如上图的边 BC、BE、DE 就是横切边
◼ 切分定理：给定任意切分，横切边中权值最小的边必然属于最小生成树
1.普利姆（prim）算法
Prim算法: 归并顶点，与边数无关，适于稠密网
设连通网络 N = { V, E }
♦ 从某顶点 u0 出发，选择与它关联的具有最小权值的边(u0, v)，将其顶点加入到生成树的顶点集合U中
♦ 每一步从一个顶点在U中，而另一个顶点不在U中的各条边中选择权值最小的边(u, v),把它的顶点加入到U中
♦ 直到所有顶点都加入到生成树顶点集合U中为止
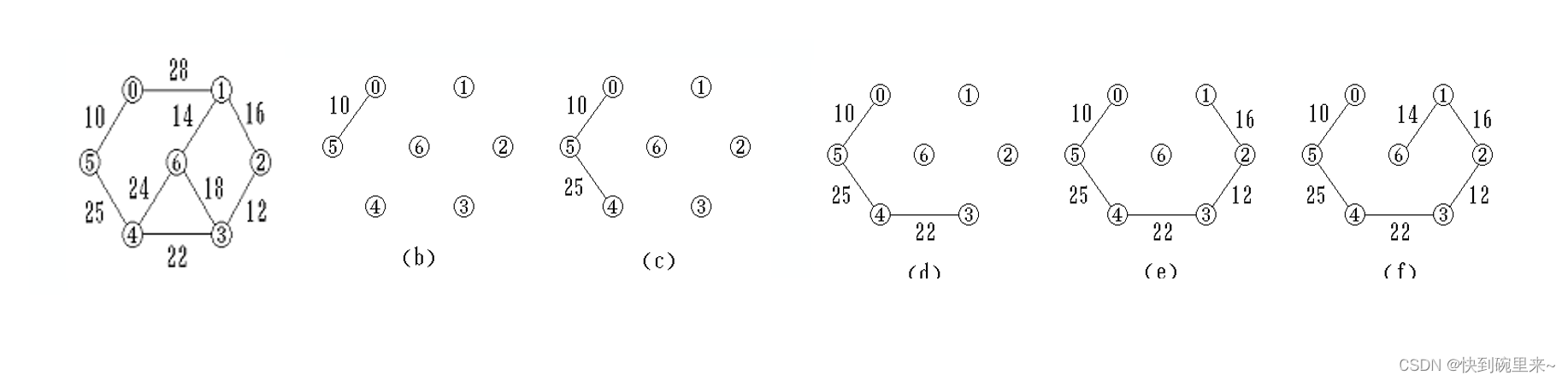
注意：在归并点的过程中不能形成环
2.克鲁斯尔(kruskal)算法
Kruskal算法：归并边，适于稀疏网
设连通网络 N = { V, E }
1. 构造一个只有 n 个顶点，没有边的非连通图 T = { V, }, 每个顶点自成一个连通分量
2. 在 E 中选最小权值的边,若该边的两个顶点落在不同的连通分量上，则加入 T 中；否则舍去，重新选择
3. 重复下去，直到所有顶点在同一连通分量上为止
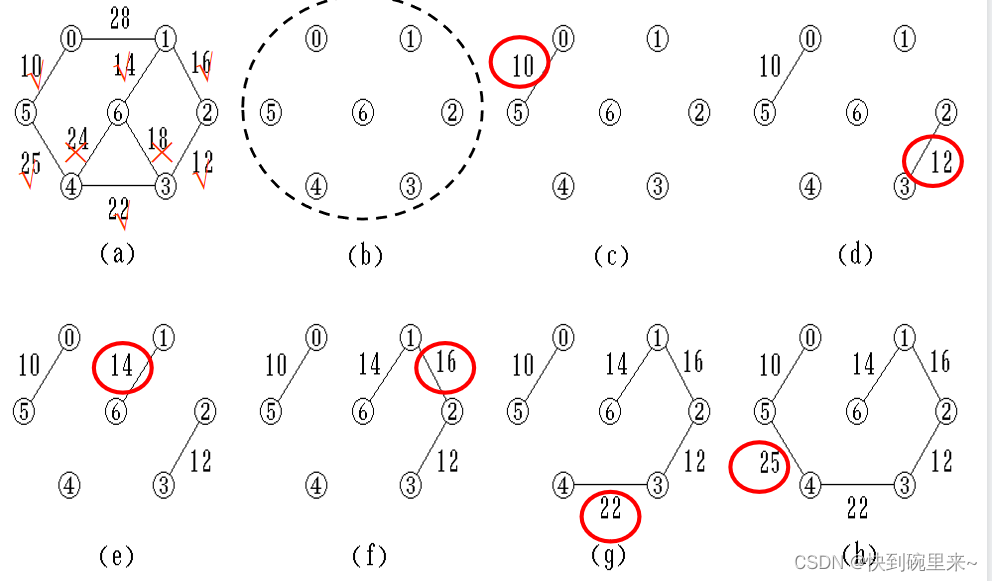
注意：在归并边的过程中不能形成环
四.最短路径
🥳最短路径是指两个顶点之间权值最小的路径（有向图，无向图均适用，不能有负权环）
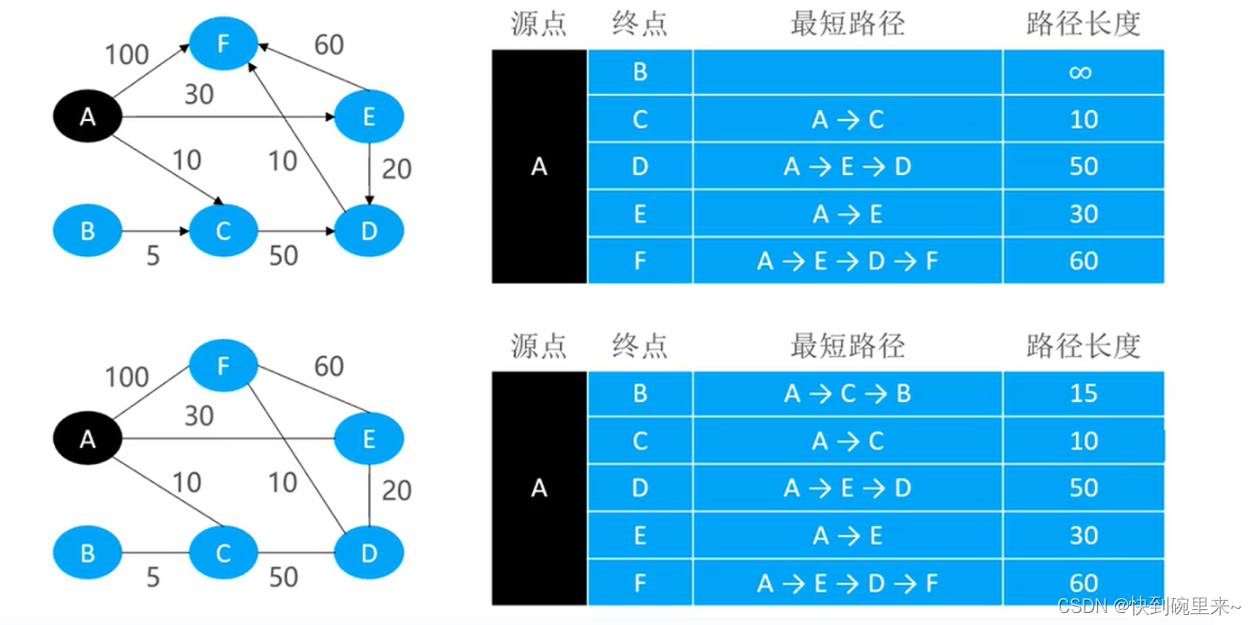
（1）最短路径之无权图
无权图相当于各个边权值为1的有权图
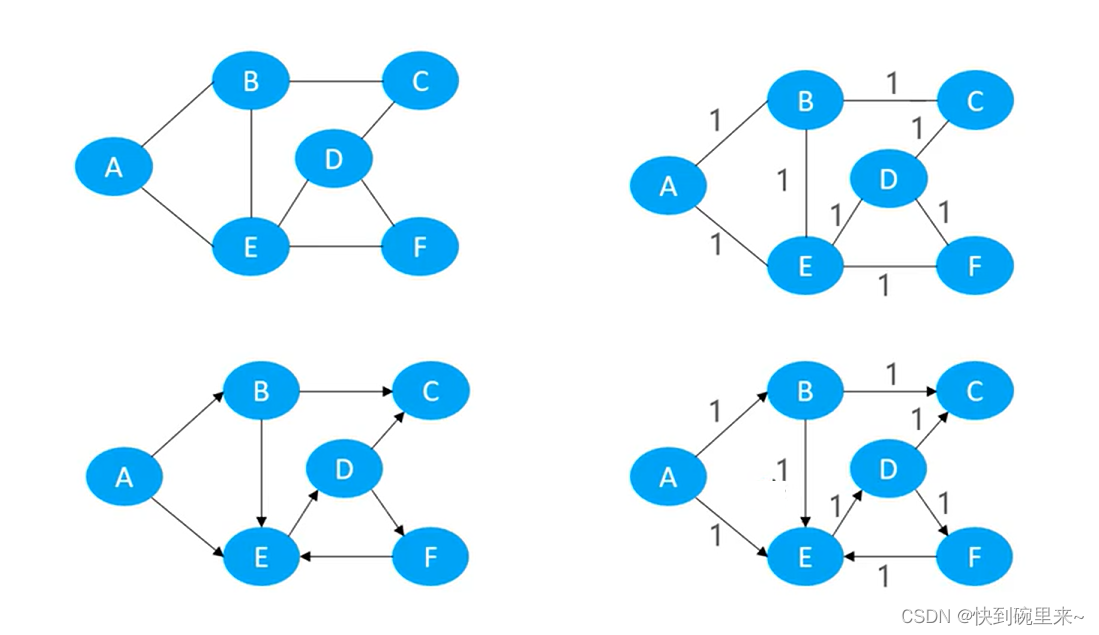
（2）最短路径之负权环
有环且存在负权边即为负权环
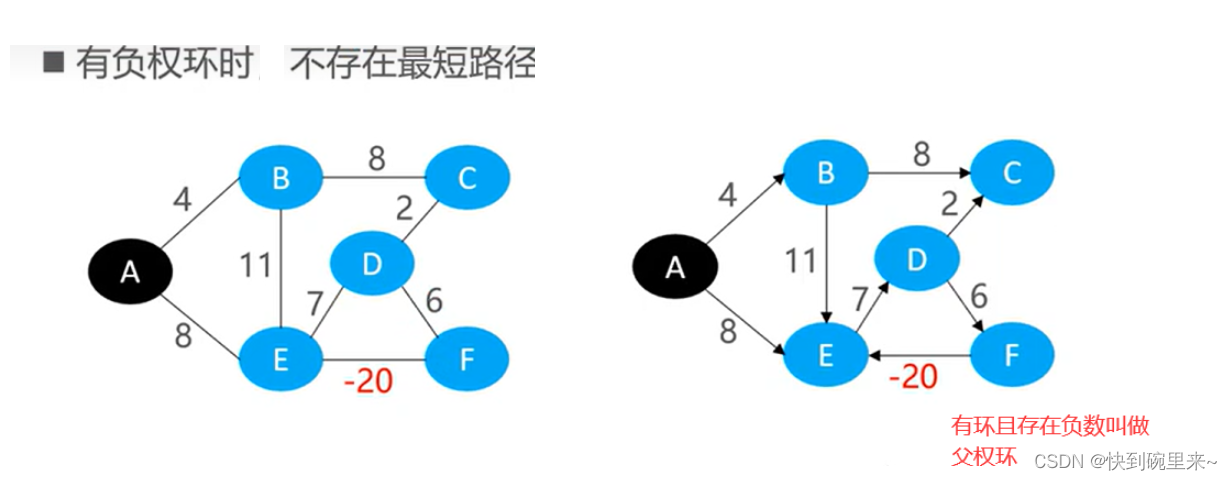
算法实现
1 .Dijkstra（迪杰斯特拉算法）
Dijkstra 属于单源最短路径算法，用于计算一个顶点到其他所有顶点的最短路径
(所谓单源最短路径就是起点是确定的终点是任意一个节点，通过迪杰斯特拉算法可以计算出从起点出发到任意一个节点的最短路径)。
🌀使用前提：不能有负权边
🌀时间复杂度：可优化至 O( ElogV) ，E 是边数量，V 是节点数量
🌀 由荷兰的科学家 Edsger Wybe Dijkstra 发明，曾在1972年获得图灵奖
算法思想具体形象化（缓慢拉绳子案例）
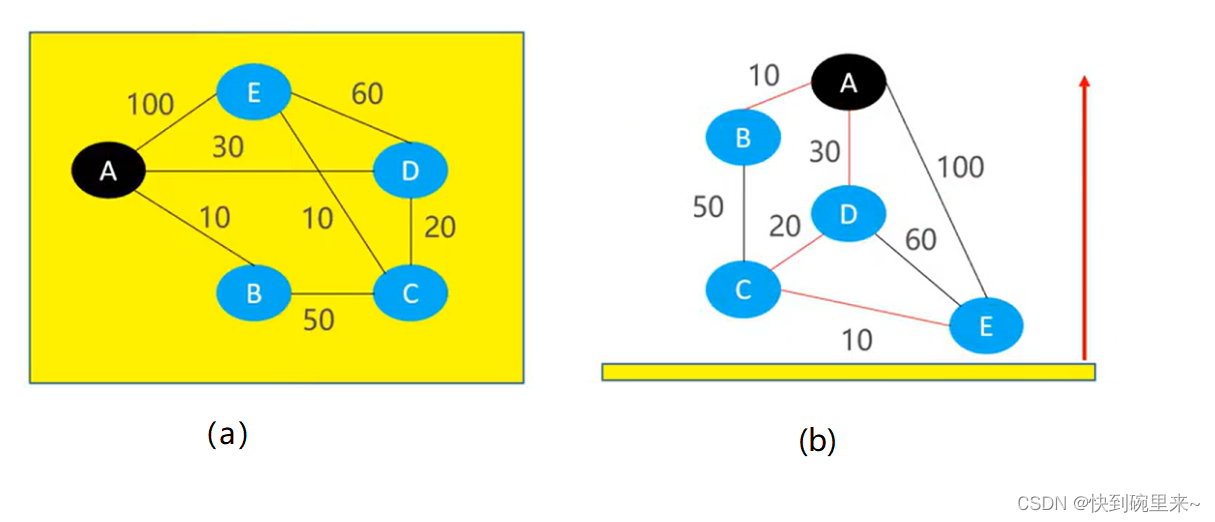
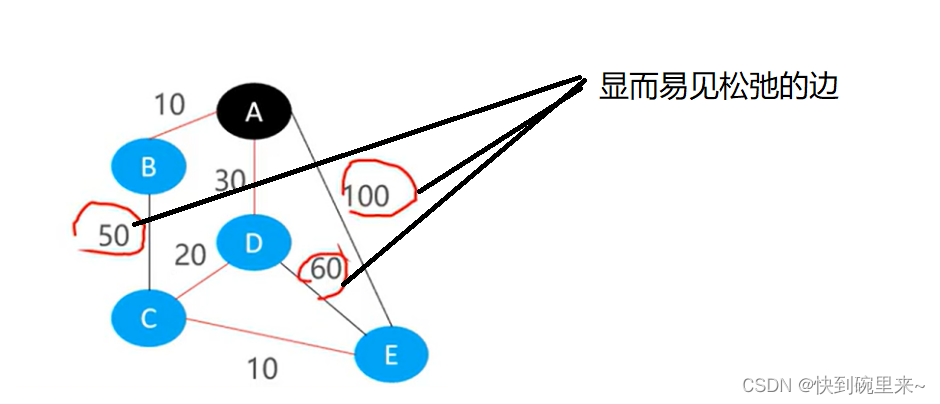
如下图（a）所示是一张无向图，最短路径的起点设为A。假设一种场景我们将每一个节点想象成一个小石头块。节点之间的边想象成连接石头的绳子。我们将该图平铺在桌子上，如图(b)所示是一张俯视图。黄色的底边是桌子。我们缓缓拉起A石子，紧接着别的石子也陆陆续续被拉起来。等到石头全部被拉上来之后紧绷的绳子就是最短路径。
在图被完全拉起的过程中其实是有路径的更新，一开始紧绷的绳子，在后续石子被拉起来后可能一开始紧绷的绳子后来就变的松弛。
◼ 有一个很关键的信息
✓后离开桌面的小石头
✓ 都是被先离开桌面的小石头拉起来的
//每个节点的value对应一条最短路径
public Map<V, pathInfo<V,E>> digkstra(V begin) {
Vertex<V,E> beginVertex=vertexes.get(begin);
if(beginVertex==null)return null;
//存放目前已经确定的最短路径的边
Map<V,pathInfo<V,E>> selectedPaths=new HashMap<>();
Map<Vertex<V,E>,pathInfo<V,E>> paths=new HashMap<>();
//初始化paths,初始化路径和路径权值和
for(Edge<V,E>edge:beginVertex.outEdges){
pathInfo<V,E>path=new pathInfo<>();
path.weight=edge.weight;
path.edgeInfos.add(edge.toInfo());
paths.put(edge.to,path);
}
//遍历vertex的出度的边更新路径表
//找出从该点出发的最小路径
while(!paths.isEmpty()){
Map.Entry<Vertex<V,E>,pathInfo<V,E>> min=getMinPath(paths);
Vertex<V,E> minVertex=min.getKey();
//获得到节点的最小路径后
//1.将节点加入到selectedPath中
//2.继续遍历该节点的outEdges()找到他连接的节点看看是不是需要更新路径
selectedPaths.put(minVertex.val,min.getValue());
paths.remove(minVertex);//已经遍历过了z'x
for(Edge<V,E> edge:minVertex.outEdges){
if(selectedPaths.containsKey(edge.to)||edge.to.equals(beginVertex))continue;
relaxFordigkstra(min.getValue(),paths,edge);
}
}
// selectedPaths.remove(begin);//针对无向图的改进方法二
return selectedPaths;
}
public void relaxFordigkstra( pathInfo<V,E> fromPath,Map<Vertex<V,E>,pathInfo<V,E>> paths,Edge<V,E> edge){
E newValue=weightManager.add(fromPath.weight,edge.weight);
//获得路径信息然后间接获得路径的权值
pathInfo<V,E> oldPath=paths.get(edge.to);
//压根不需要更新路径
if(oldPath!=null&&weightManager.compare(newValue,oldPath.weight)>=0)return ;
//之前没有路径
if(oldPath==null){
oldPath=new pathInfo<>();
paths.put(edge.to,oldPath);
}else {
oldPath.edgeInfos.clear();
}
//这样安排就是为了可以不用在新new一个pathInfo
oldPath.weight=newValue;
oldPath.edgeInfos.addAll(fromPath.edgeInfos);
paths.put(edge.to,oldPath);
}
由于代码的关联性很强，所以理解起来很困难，可以到的我的代码仓库查看详细代码。gitee代码仓库（点这里呦~）
2. Bellman-Ford（贝尔曼-福特算法）
Bellman-Ford 也属于单源最短路径算法，支持负权边，还能检测出是否有负权环
💖💖算法原理：对每一条边进行 V – 1 次松弛操作（ V 是节点数量），得到所有可能的最短路径
💖💖时间复杂度：O （EV） ，E 是边数量，V 是节点数量
下图的最好情况是恰好从左到右的顺序对边进行松弛操作
对所有边仅需进行 1 次松弛操作就能计算出A到达其他所有顶点的最短路径
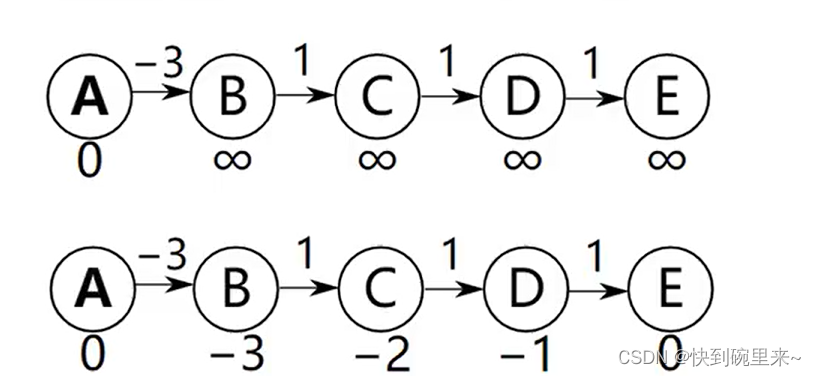最坏情况是恰好每次都从右到左的顺序对边进行松弛操作
对所有边需进行 V – 1 次松弛操作才能计算出A到达其他所有顶点的最短路径
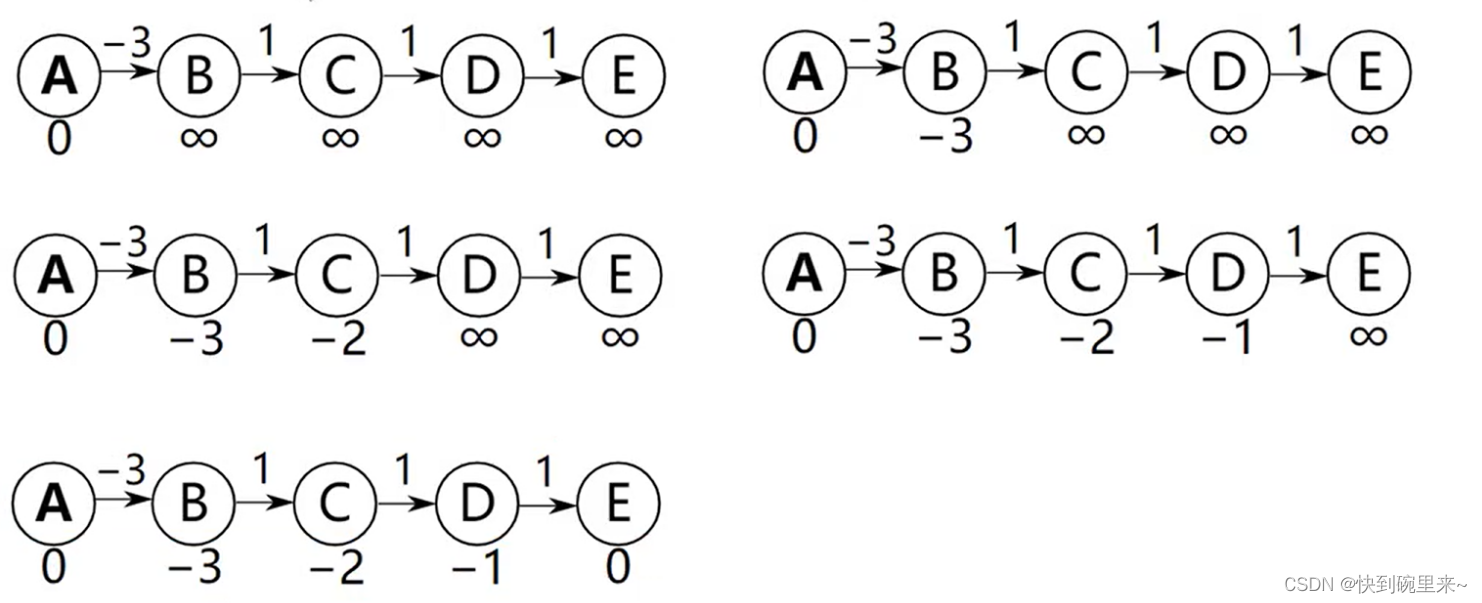
public void relaxForbellmanFord(pathInfo<V,E> fromPath,Map<V,pathInfo<V,E>> paths,Edge<V,E> edge){
E newValue=weightManager.add(fromPath.weight,edge.weight);
//获得路径信息然后间接获得路径的权值
pathInfo<V,E> oldPath=paths.get(edge.to.val);
//压根不需要更新路径
if(oldPath!=null&&weightManager.compare(newValue,oldPath.weight)>=0)return ;
//之前没有路径
if(oldPath==null){
oldPath=new pathInfo<>();
paths.put(edge.to.val,oldPath);
}else {
oldPath.edgeInfos.clear();
}
//这样安排就是为了可以不用在新new一个pathInfo
oldPath.weight=newValue;
oldPath.edgeInfos.addAll(fromPath.edgeInfos);
paths.put(edge.to.val,oldPath);
}
public Map<V,pathInfo<V,E>> bellmanFord(V begin){
Vertex<V,E> beginVertex=vertexes.get(begin);
if(beginVertex==null) return null;
Map<V,pathInfo<V,E>> selectedPath=new HashMap<>();
pathInfo<V,E> beginPath=new pathInfo<>();
beginPath.weight=weightManager.zero();
selectedPath.put(begin,beginPath);
int count=vertexes.size()-1;
for(int i=0;i<count;i++){
for(Edge edge:edges){
pathInfo<V,E> fromPath=selectedPath.get(edge.from.val);
//fromPath可能为Null,松弛失败->前一个节点的最短路径还没有确定
//selectedPath本身就是空的，所以要一开始就添加一个意义上是A->A的路径，但是不能直接添加字符串因为会造成A->A->b的现象
//所以要定义一个意义上为0的权值概念，但是权值是泛型，所以我在接口添加zero方法用来解释不通类型0权值的含义
if(fromPath==null)continue;
relaxForbellmanFord(fromPath,selectedPath,edge);
}
}
return selectedPath;
}
五.拓扑排序
1.AOV网（Activity On Vertex Network）
一项大的工程常被分为多个小的子工程
✓ 子工程之间可能存在一定的先后顺序，即某些子工程必须在其他的一些子工程完成后才能开始
◼ 在现代化管理中，人们常用有向图来描述和分析一项工程的计划和实施过程，子工程被称为活动（Activity）
✓ 以顶点表示活动、有向边表示活动之间的先后关系，这样的图简称为 AOV 网
◼ 标准的AOV网必须是一个有向无环图（Directed Acyclic Graph，简称 DAG）
2.拓扑排序原理
◼ 前驱活动：有向边起点的活动称为终点的前驱活动
只有当一个活动的前驱全部都完成后，这个活动才能进行
◼ 后继活动：有向边终点的活动称为起点的后继活动
◼ 什么是拓扑排序？
将 AOV 网中所有活动排成一个序列，使得每个活动的前驱活动都排在该活动的前面
比如上图的拓扑排序结果是：A、B、C、D、E、F 或者 A、B、D、C、E、F （结果并不一定是唯一的）
Override
public List<V> topologicalSort() {
List<V> list=new ArrayList<>();
Queue<Vertex<V,E>> queue=new LinkedList();
//将一开始为度不为零的节点与同他它的入度形成映射
Map<Vertex<V,E>,Integer> map=new HashMap<>();
//初始化表:入度为0的都放入队列，入度不为0的放入表中等待更新
vertexes.forEach((V v,Vertex<V,E> ver)->{
int ins=ver.inEdges.size();
if(ins==0){
queue.offer(ver);
}else{
map.put(ver,ins);
}
});
while(!queue.isEmpty()){
Vertex<V,E> vertex=queue.poll();
//加入到输出表中
list.add(vertex.val);
for(Edge<V,E> edge:vertex.outEdges)
{
//原本节点的入度减一
int in=map.get(edge.to)-1;
//如果入度减一后变为度为0
if(in==0){
queue.offer(edge.to);
}else{
//入过不为0则更新入度表
map.put(edge.to,in);
}
}
}
return list;
}
