Problem - 1225C - Codeforces
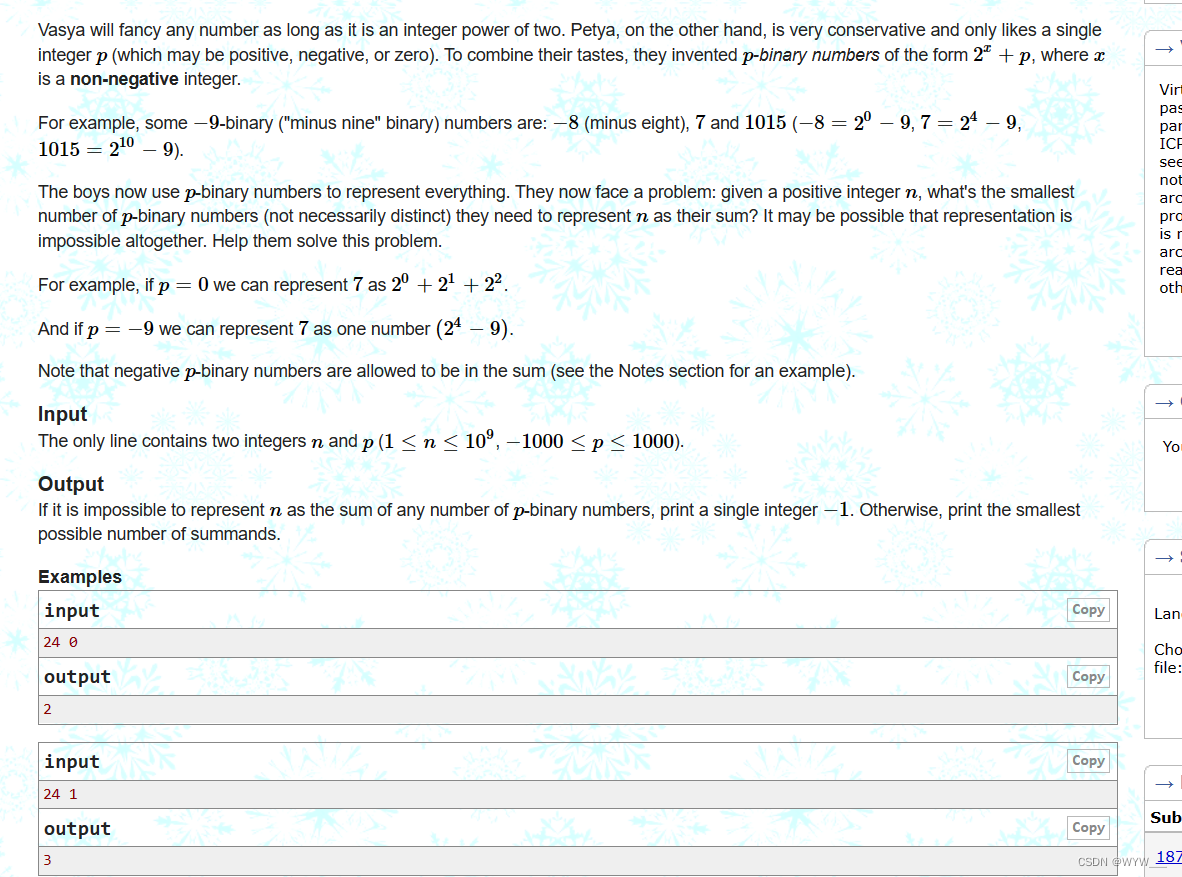
Vasya会看中任何数字,只要它是2的整数次方。另一方面,Petya非常保守,只喜欢单一的整数p(可以是正数、负数或零)。为了结合他们的口味,他们发明了2x+p形式的p-二进制数,其中x是一个非负整数。
例如,一些-9-二进制("减九 "二进制)的数字是。-8(减八),7和1015(-8=20-9,7=24-9,1015=210-9)。
男孩们现在用p-二进制数来表示一切。他们现在面临一个问题:给定一个正整数n,他们需要最小数量的p-二进制数(不一定是不同的)来表示n的和?有可能完全无法表示。帮助他们解决这个问题。
例如,如果p=0,我们可以把7表示为20+21+22。
而如果p=9,我们可以把7表示为一个数字(24-9)。
请注意,负的p-二进制数字是允许出现在总和中的(见注释部分的例子)。
输入
唯一一行包含两个整数n和p(1≤n≤109,-1000≤p≤1000)。
输出
如果不可能将n表示为任何数量的p二进制数之和,则打印一个整数-1。否则,打印最小的可能的和数。
例子
inputCopy
24 0
outputCopy
2
输入复制
24 1
输出拷贝
3
输入复制
24 -1
输出拷贝
4
输入复制
4 -7
输出拷贝
2
输入复制
1 1
输出拷贝
-1
注意
0-二进制数只是普通的二进制幂,因此在第一个例子中,我们可以表示24=(24+0)+(23+0)。
在第二个例子中,我们可以表示24=(24+1)+(22+1)+(20+1)。
在第三个例子中,我们可以表示24=(24-1)+(22-1)+(22-1)+(22-1)。请注意,重复的总和是允许的。
在第四个例子中,我们可以表示4=(24-7)+(21-7)。注意第二个和是负数,这是允许的。
在第五个例子中,不可能表示。
题解:
最终答案应该是k个二进制数+k*p = n
我们转换一下形式就变成了 k个二进制数 = n - k*p
我们直接从一开始枚举k,看剩下的x = n - k*p是否能由几个二进制数组成
首先x肯定要大于k,因为二进制数最小为2^0 = 1,所以x >= k
其次x中二进制位1的数目应该小于k,因为如果大于k,k个二进制数是无法组成的
如果可以组成直接break
枚举到x < 0时要break,因为剩下的数肯定也不行
#include<iostream>
#include<algorithm>
#include<string>
#include<queue>
#include<vector>
#include<map>
#include<cstring>
#include<cmath>
#include<set>
using namespace std;
#define int long long
typedef pair<int,int> PII;
int check(int s)
{
int cnt = 0;
while(s)
{
if(s%2)
cnt++;
s/=2;
}
return cnt;
}
void solve()
{
int ans = 1e18;
int n,p;
cin >>n >> p;
for(int i = 1;;i++)
{
int t = n - p*i;
if(t >= i&&check(t) <= i)
{
ans = i;
break;
}
if(t < 0)
break;
}
if(ans == 1e18)
cout<<-1;
else
cout<<ans;
}
//cbc cbb
//7 3 1
//6 5 4
signed main(){
// ios::sync_with_stdio(false);
// cin.tie(0);
// cout.tie(0);
int t = 1;
// cin >> t;
while(t--)
{
solve();
}
}
//5
//2 4 6 8 10 7 9 5 3 1
//1 3 5 7 9 6 8 4 2
//2 4 1 3