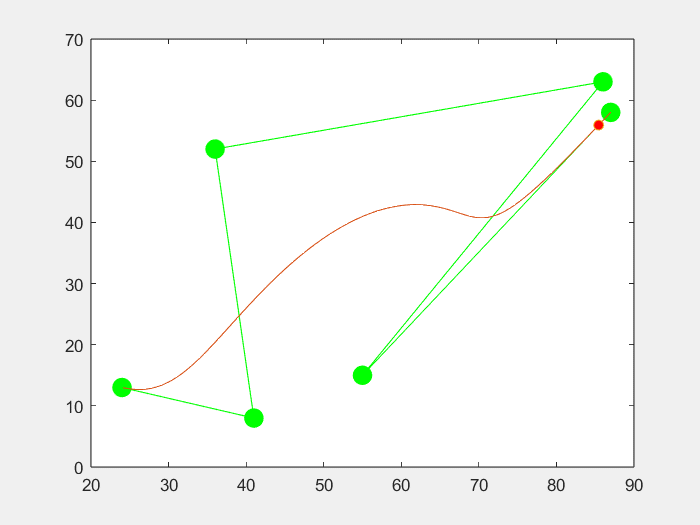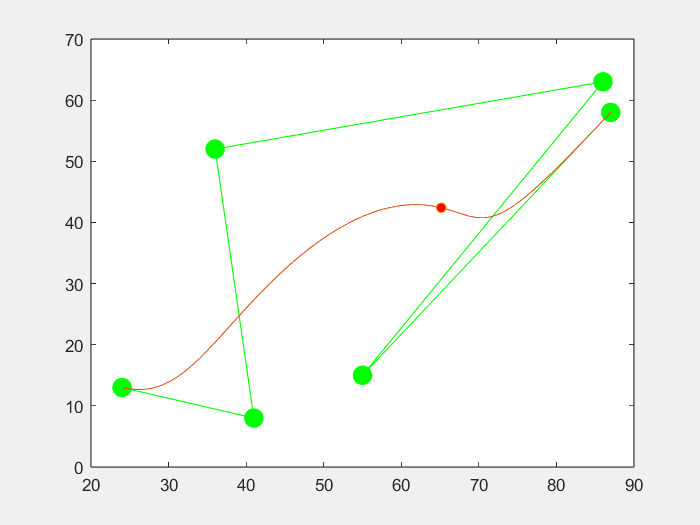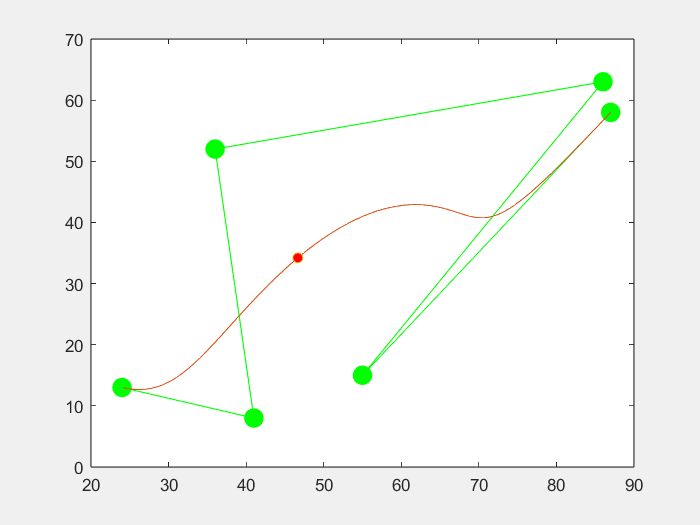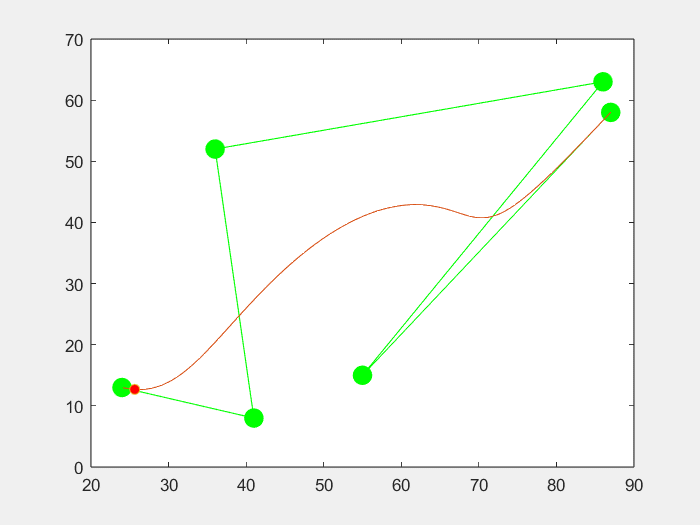
RMSE:均方根误差是回归线拟合数据点的程度的度量。RMSE也可以解释为残差中的标准差。
考虑给定的数据点:(1,1),(2,2),(2,3),(3,6)。
让我们把上面的数据点分解成一维列表。
输入
x = [1, 2, 2, 3]
y = [1, 2, 3, 6]
回归图
import matplotlib.pyplot as plt
import math
# plotting the points
plt.plot(x, y)
# naming the x axis
plt.xlabel('x - axis')
# naming the y axis
plt.ylabel('y - axis')
# giving a title to my graph
plt.title('Regression Graph')
# function to show the plot
plt.show()

平均值计算
#在下一步中,我们将找到最佳拟合线的方程
#我们将使用线性代数的点斜率来找到回归方程
#点斜率形式表示为y = mx + c
#其中m是斜率平均值(y变化)/(x变化)
#c是常数,它表示直线与y轴相交的点
# calculate Xmean and Ymean
ct = len(x)
sum_x = 0
sum_y = 0
for i in x:
sum_x = sum_x + i
x_mean = sum_x / ct
print('Value of X mean', x_mean)
for i in y:
sum_y = sum_y + i
y_mean = sum_y / ct
print('value of Y mean', y_mean)
输出
Value of X mean 2.0
value of Y mean 3.0
直线方程
#下面是用数学术语求直线方程的过程
#线的斜率为2.5
#计算c,找出方程
m = 2.5
c = y_mean - m * x_mean
print('Intercept', c)
输出
Intercept -2.0
均方误差
# 我们的回归方程如下:
# y_pred = 2.5x-2.0
from sklearn.metrics import mean_squared_error
y =[1, 2, 3, 6]
y_pred =[0.5, 3, 3, 5.5]

# 由sklearn计算的均方根
mse1 = math.sqrt(mean_squared_error(y, y_pred))
print('Root mean square error', mse1)
# 另一种求RMSE的方法
# 是通过在mean_squared_error中设置squared属性False
mse2 = mean_squared_error(y, y_pred, squared=False)
print('Root mean square error', mse2)
输出
Root mean square error 0.6123724356957945
RMSE计算
# y_pred1 = 1-(2.5 * 1-2.0)= 0.5
r1 = 1-(2.5 * 1-2.0)
#(2, 2) r2 = 2, x = 2
# y_pred2 = 2-(2.5 * 2-2.0)=-1
r2 = 2-(2.5 * 2-2.0)
#(2, 3) r3 = 3, x = 2
# y_pred3 = 3-(2.5 * 2-2.0)= 0
r3 = 3-(2.5 * 2-2.0)
#(3, 6) r4 = 4, x = 3
# y_pred4 = 6-(2.5 * 3-2.0)=.5
r4 = 6-(2.5 * 3-2.0)
# 从上面的计算中,我们得到了残差值
residuals =[0.5, -1, 0, .5]
N = 4
rmse = math.sqrt((r1**2 + r2**2 + r3**2 + r4**2)/N)
print('Root Mean square error using maths', rmse)

输出
Root Mean square error using maths 0.6123724356957945

R平方误差
# SEline =(y1-(mx1 + b)**2 + y2-(mx2 + b)**2...+yn-(mxn + b)**2)
# SE_line =(1-(2.5 * 1+(-2))**2 + (2-(2.5 * 2+(-2))**2) +(3-(2.5*(2)+(-2))**2) + (6-(2.5*(3)+(-2))**2))
val1 =(1-(2.5 * 1+(-2)))**2
val2 =(2-(2.5 * 2+(-2)))**2
val3 =(3-(2.5 * 2+(-2)))**2
val4 =(6-(2.5 * 3+(-2)))**2
SE_line = val1 + val2 + val3 + val4
print('val', val1, val2, val3, val4)
# y_var =(y1-ymean)**2+(y2-ymean)**2...+(yn-ymean)2
y =[1, 2, 3, 6]
y_var =(1-3)**2+(2-3)**2+(3-3)**2+(6-3)**2
SE_mean = y_var
r_squared = 1-(SE_line / SE_mean)
print('Rsquared error', r_squared)
输出
('val', 0.25, 1.0, 0.0, 0.25)
('Rsquared error', 0.8928571428571429)
使用sklearn计算R平方误差
from sklearn.metrics import r2_score
r2_score(y, y_pred)
输出
0.8928571428571429