matlab实践（十）：贝塞尔曲线

news2025/1/23 22:38:55

1.贝塞尔曲线

贝塞尔曲线的原理是基于贝塞尔曲线的数学表达式和插值算法。

贝塞尔曲线的数学表达式可以通过控制点来定义。对于二次贝塞尔曲线，它由三个控制点P0、P1和P2组成，其中P0和P2是曲线的起点和终点，P1是曲线上的一个中间点。曲线上的每个点可以通过参数t在0到1之间的取值来计算，公式如下：

B(t) = (1-t)^2 * P0 + 2 * t * (1-t) * P1 + t^2 * P2

其中，B(t)表示曲线上的点，t表示参数值，(1-t)表示参数值的补数。

对于三次贝塞尔曲线，它由四个控制点P0、P1、P2和P3组成，其中P0和P3是曲线的起点和终点，P1和P2是曲线上的两个中间点。曲线上的每个点可以通过参数t在0到1之间的取值来计算，公式如下：

B(t) = (1-t)^3 * P0 + 3 * t * (1-t)^2 * P1 + 3 * t^2 * (1-t) * P2 +
t^3 * P3

贝塞尔曲线的插值算法可以通过递归的方式来计算。对于二次贝塞尔曲线，可以通过将两个二次贝塞尔曲线的控制点作为新的控制点，再次应用贝塞尔曲线的计算公式来得到更高阶的曲线。同样地，对于三次贝塞尔曲线，可以通过将两个三次贝塞尔曲线的控制点作为新的控制点，再次应用贝塞尔曲线的计算公式来得到更高阶的曲线。

贝塞尔曲线的优点是可以通过调整控制点的位置来改变曲线的形状，同时保持曲线的平滑性。这使得贝塞尔曲线在计算机图形学和计算机辅助设计中得到广泛应用，例如绘制曲线、路径动画、字体设计等。

2.代码

贝塞尔曲线本质上是一个递推公式。
p ( i , j ) = ( 1 − u ) × p ( i − 1 , j ) + u × p ( i − 1 , j − 1 ) \color{red}{p(i,j)=(1-u)\times p(i-1,j)+u\times p(i-1,j-1)} p(i,j)=(1−u)×p(i−1,j)+u×p(i−1,j−1)
上述递推公式中 , i 表示贝塞尔曲线的阶数 , j 表示贝塞尔曲线中的点个数 ( 包含起止点 + 控制点 ) , u 表示比例取值范围 0 ~ 1 ;

function points = computeCubicBezierCurve(controlPoints, numPoints)
    numControlPoints = size(controlPoints, 2);
    t = linspace(0, 1, numPoints); % 在0到1之间生成numPoints个等间距的参数值
    points = zeros(2, numPoints); % 存储曲线上的点坐标
    
    for i = 1:numPoints
        B = zeros(2, 1);
        for j = 1:numControlPoints
            B = B + nchoosek(numControlPoints-1, j-1) * t(i)^(j-1) * (1 - t(i))^(numControlPoints-j) * controlPoints(:, j);
        end
        points(:, i) = B; % 存储点坐标
    end
end

这是用彗星图画的

P=randi(100,2,60);
position=computeCubicBezierCurve(P,100);

X=position(1,:);
Y=position(2,:);
figure(1);
h=gca;
plot(P(1,:),P(2,:),'g.-','MarkerSize',40);
c={'起点'};
text(P(1,1),P(2,1),c,'HorizontalAlignment','left')
hold on

text(P(1,end),P(2,end),'终点','HorizontalAlignment','left')
hold on

mycomet(h,X,Y,0.8)

2.1总代码

clc;clear;
% fps = 40;
% myVideo = VideoWriter('test2.avi'); 
% myVideo.FrameRate = fps; 
% open(myVideo); 
% P0=[1,2];
% P1=[5,8];
% P2=[10,10];
% P=[P0;P1;P2];
% X=@(t)(1-t).^2.*P0(1)+2.*t.*(1-t)*P1(1)+t.^2*P2(1);
% Y=@(t)(1-t).^2.*P0(2)+2.*t.*(1-t)*P1(2)+t.^2*P2(2);
% x1=@(t)(1-t).*P0(1)+t.*P1(1);
% y1=@(t)(1-t).*P0(2)+t.*P1(2);
% x2=@(t)(1-t).*P1(1)+t.*P2(1);
% y2=@(t)(1-t).*P1(2)+t.*P2(2);
% t=0:0.01:1;
% X=X(t);
% Y=Y(t);
% x1=x1(t);
% y1=y1(t);
% x2=x2(t);
% y2=y2(t);
P=randi(100,2,6);
position=computeCubicBezierCurve(P,100);

X=position(1,:);
Y=position(2,:);
% figure(1);
% h=gca;
% plot(P(1,:),P(2,:),'g.-','MarkerSize',40);
% c={'起点'};
% text(P(1,1),P(2,1),c,'HorizontalAlignment','left')
% hold on
% 
% text(P(1,end),P(2,end),'终点','HorizontalAlignment','left')
% hold on
% 
% mycomet(h,X,Y,0.8)

% figure
% for k = 1:101
%     plot(P(1,:),P(2,:),'k.-','MarkerSize',40),hold on
%     plot(X(k),Y(k),'r.'),hold on
%     % plot(x1(k),y1(k),'g.'),hold on
%     % plot(x2(k),y2(k),'g.'),hold on
%     % plot([x2(k),x1(k)],[y2(k),y1(k)],'y-'),hold on
%     axis([min(P(1,:)),max(P(1,:)),min(P(2,:)),max(P(2,:))]),drawnow
%     frame = getframe(gcf);
%     im = frame2im(frame); 
%     writeVideo(myVideo,im); 
% end
% close(myVideo); 
plot(P(1,:),P(2,:),'g.-','MarkerSize',40),hold on
plot(X,Y)
hold on
p = plot(X(1),Y(1),'o','MarkerFaceColor','red');
hold off
axis manual
pic_num=1;
for k = 2:101
    p.XData = X(k);
    p.YData = Y(k);
    
    F=getframe(gcf);
    I=frame2im(F);
    [I,map]=rgb2ind(I,256);
    if pic_num==1
    imwrite(I,map,'test.gif','gif','Loopcount',inf,'DelayTime',0.2);
    elseif mod(pic_num,3)==1
    imwrite(I,map,'test.gif','gif','WriteMode','append','DelayTime',0.2);
    end
    pic_num = pic_num + 1;
 
    drawnow limitrate
end
function mycomet(varargin)
%COMET  Comet-like trajectory.
%   COMET(Y) displays an animated comet plot of the vector Y.
%   COMET(X,Y) displays an animated comet plot of vector Y vs. X.
%   COMET(X,Y,p) uses a comet of length p*length(Y).  Default is p = 0.10.
%
%   COMET(AX,...) plots into AX instead of GCA.
%
%   Example:
%       t = -pi:pi/200:pi;
%       comet(t,tan(sin(t))-sin(tan(t)))
%
%   See also COMET3.

%   Charles R. Denham, MathWorks, 1989.
%   Copyright 1984-2022 The MathWorks, Inc.

% Parse possible Axes input
nnn=0.05;

[ax,args,nargs] = axescheck(varargin{:});
if nargs < 1
    error(message('MATLAB:narginchk:notEnoughInputs'));
elseif nargs > 3
    error(message('MATLAB:narginchk:tooManyInputs'));
end

% Parse the rest of the inputs
bodyLengthProportion = 0.10;
if nargs < 2, x = args{1}; y = x; x = 1:length(y); end
if nargs == 2, [x,y] = deal(args{:}); end
if nargs == 3, [x,y,bodyLengthProportion] = deal(args{:}); end

if ~isscalar(bodyLengthProportion) || ~isreal(bodyLengthProportion) ||  bodyLengthProportion < 0 || bodyLengthProportion >= 1
    error(message('MATLAB:comet:InvalidP'));
end

x = matlab.graphics.chart.internal.datachk(x);
y = matlab.graphics.chart.internal.datachk(y);

if ~isvector(x) || ~isvector(y) || numel(x) ~= numel(y)
    error(message('MATLAB:comet:XYVectorsSameLength'));
end

ax = newplot(ax);

if ~strcmp(ax.NextPlot,'add')
    % If NextPlot is 'add', assume other objects are driving the limits.
    % Otherwise, set the limits so that the axes limits don't jump around
    % during animation.
    [minx,maxx] = minmax(x);
    [miny,maxy] = minmax(y);
    if ~isa(ax,'matlab.graphics.axis.GeographicAxes') && ~isa(ax,'map.graphics.axis.MapAxes')
        axis(ax,[minx maxx miny maxy])
    else
        % Latitudes are the first axis (x) and longitudes are the second
        % axis (y).
        latmin = minx;
        latmax = maxx;
        lonmin = miny;
        lonmax = maxy;
        
        % Buffer the limits for better display.
        bufferInPercent = 5;
        f = 1 + bufferInPercent / 100;
        half = f * (latmax - latmin)/2;
        latlim = [-half, half] + (latmin + latmax)/2;
        latlim(1) = max(latlim(1), -90);
        latlim(2) = min(latlim(2),  90);
        half = f * (lonmax - lonmin)/2;
        lonlim = [-half, half] + (lonmin + lonmax)/2;
        
        geolimits(ax,latlim,lonlim)
    end
end

totalLength = length(x);
bodyLength = round(bodyLengthProportion*totalLength);

head = line('Parent',ax,'SeriesIndex_I',0,'Marker','o','LineStyle','none', ...
            'XData',x(1),'YData',y(1),'Tag','head');
body = matlab.graphics.animation.AnimatedLine('SeriesIndex_I',0,...
    'Parent',ax,'MaximumNumPoints',max(1,bodyLength),'tag','body');
tail = matlab.graphics.animation.AnimatedLine('Parent',ax, 'SeriesIndex_I',0,...
    'LineStyle','-','MaximumNumPoints',1+totalLength,'tag','tail'); %Add 1 for any extra points

if isequal(body.Color,tail.Color) && isequal(body.LineStyle, tail.LineStyle)
    body.LineStyle='--';
end

if length(x) < 2000
    updateFcn = @()drawnow;
else
    updateFcn = @()drawnow('limitrate');
end

% Grow the body
for i = 1:bodyLength
    % Protect against deleted objects following the call to drawnow.
    if ~(isvalid(head) && isvalid(body))
        return
    end
    set(head,'xdata',x(i),'ydata',y(i));
    addpoints(body,x(i),y(i));
    updateFcn();
    pause(nnn)
end

% Add a drawnow to capture any events / callbacks
drawnow

% Initialize tail with first point. The next point will be added in the
% first iteration of the primary loop below, creating the first line
% segment of the tail.
addpoints(tail,x(1),y(1));

% Primary loop
for i = bodyLength+1:totalLength
    % Protect against deleted objects following the call to drawnow.
    if ~(isvalid(head) && isvalid(body) && isvalid(tail))
        return
    end
    set(head,'xdata',x(i),'ydata',y(i));
    addpoints(body,x(i),y(i));
    
    nextTailIndex = i-bodyLength+1;
    if(nextTailIndex<=totalLength)
        addpoints(tail,x(nextTailIndex),y(nextTailIndex));
    end
    updateFcn();
    pause(nnn)
end
drawnow

% Allow tail to continue on to the full length. The last point added to the 
% tail in the primary loop above was at index (totalLength-bodyLength+1), 
% so this loop starts at the following index. 
for i = totalLength-bodyLength+2:totalLength
    % Protect against deleted objects following the call to drawnow.
    if ~isvalid(tail)
        return
    end
    addpoints(tail,x(i),y(i));
    updateFcn();
    pause(nnn)
end
drawnow

end

function [minx,maxx] = minmax(x)
minx = min(x(isfinite(x)));
maxx = max(x(isfinite(x)));
if minx == maxx
    minx = maxx-1;
    maxx = maxx+1;
end
end
function points = computeCubicBezierCurve(controlPoints, numPoints)
    numControlPoints = size(controlPoints, 2);
    t = linspace(0, 1, numPoints); % 在0到1之间生成numPoints个等间距的参数值
    points = zeros(2, numPoints); % 存储曲线上的点坐标
    
    for i = 1:numPoints
        B = zeros(2, 1);
        for j = 1:numControlPoints
            B = B + nchoosek(numControlPoints-1, j-1) * t(i)^(j-1) * (1 - t(i))^(numControlPoints-j) * controlPoints(:, j);
        end
        points(:, i) = B; % 存储点坐标
    end
end

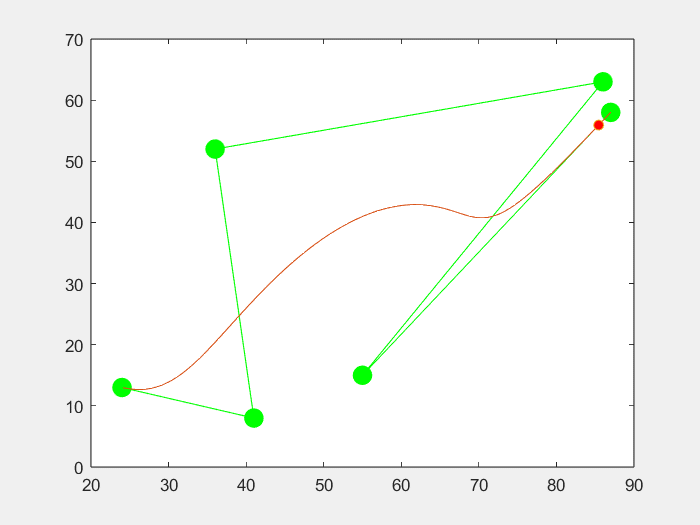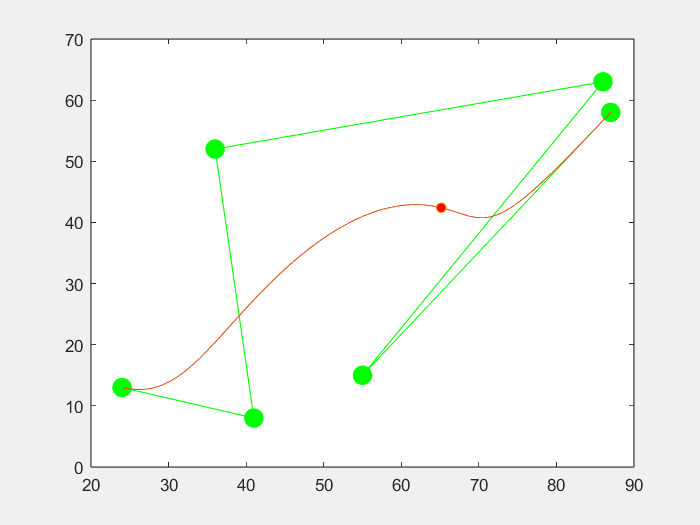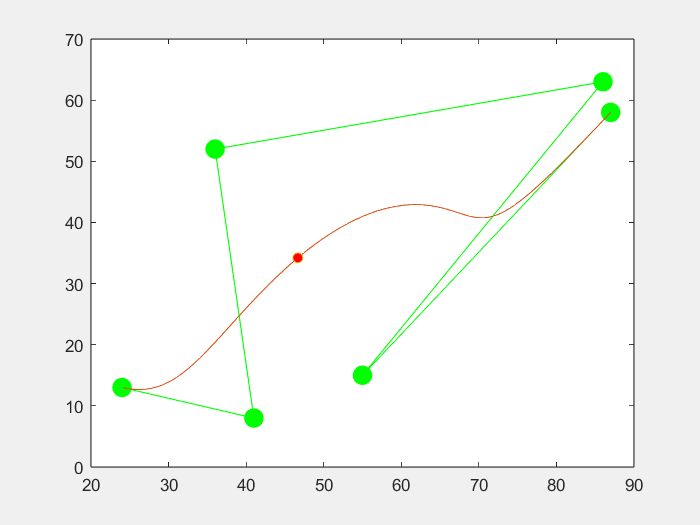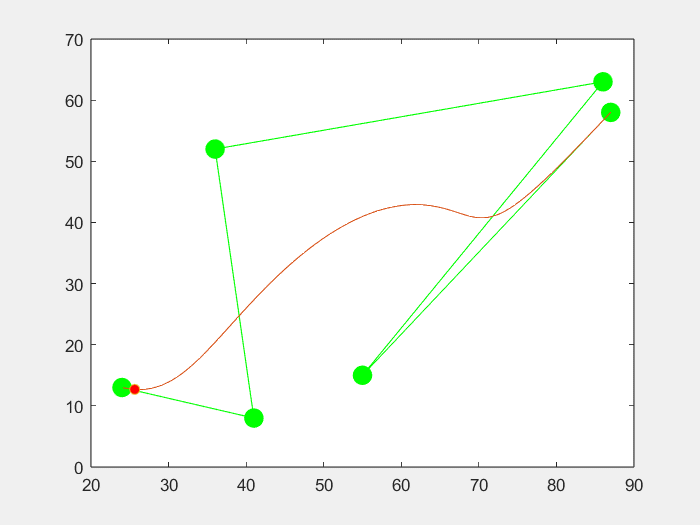
3.效果

三个点
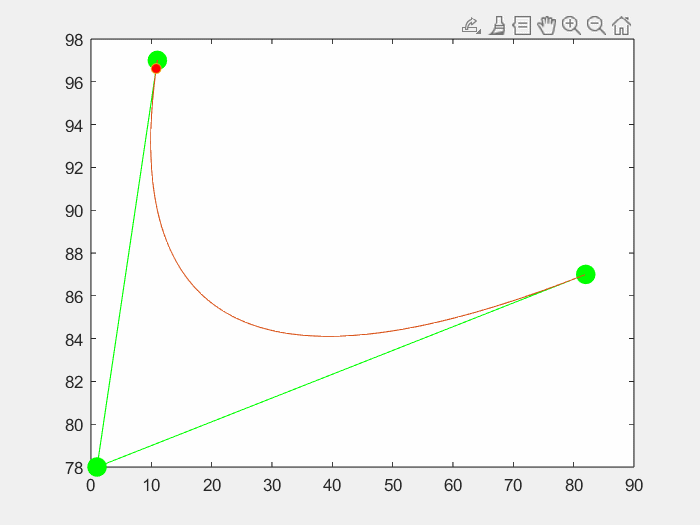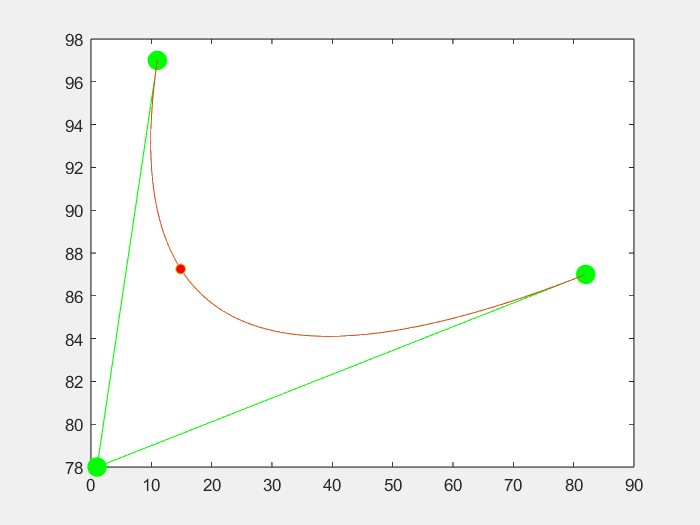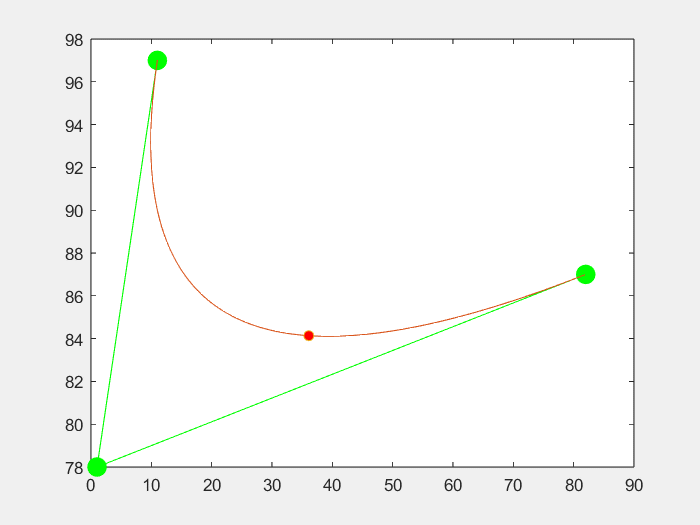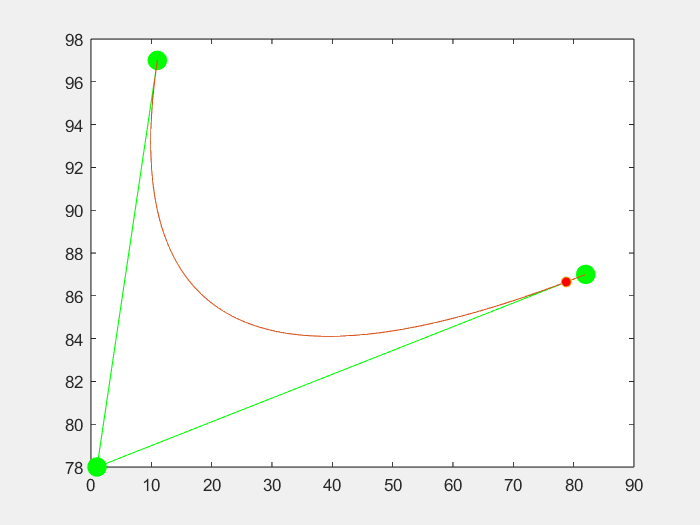
在这里插入图片描述

四个点

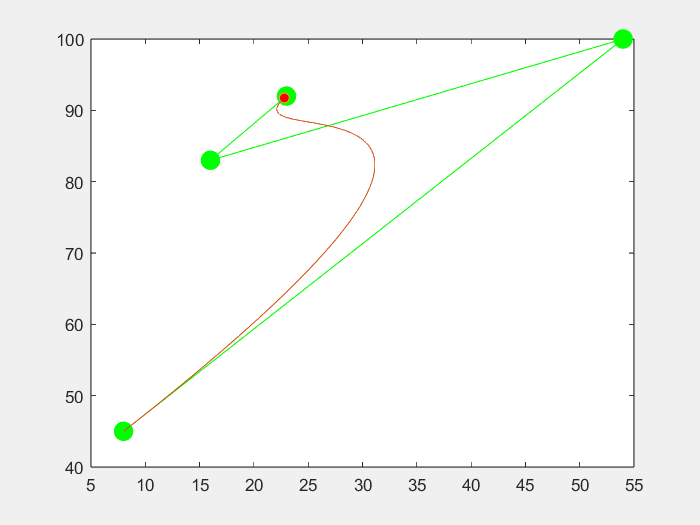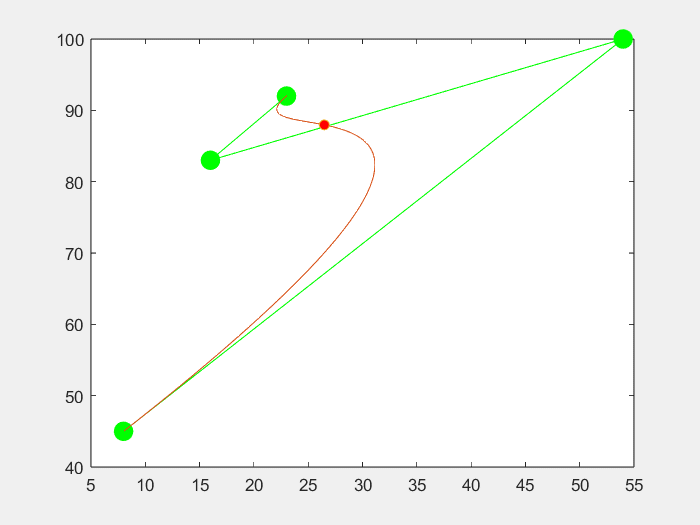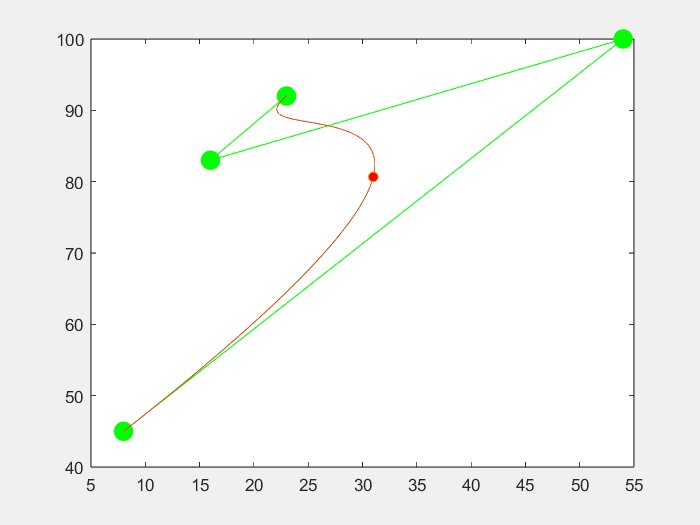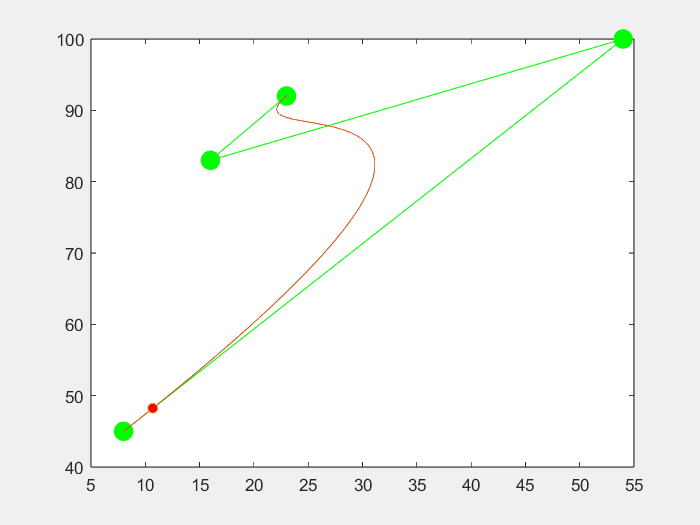
在这里插入图片描述
五个点
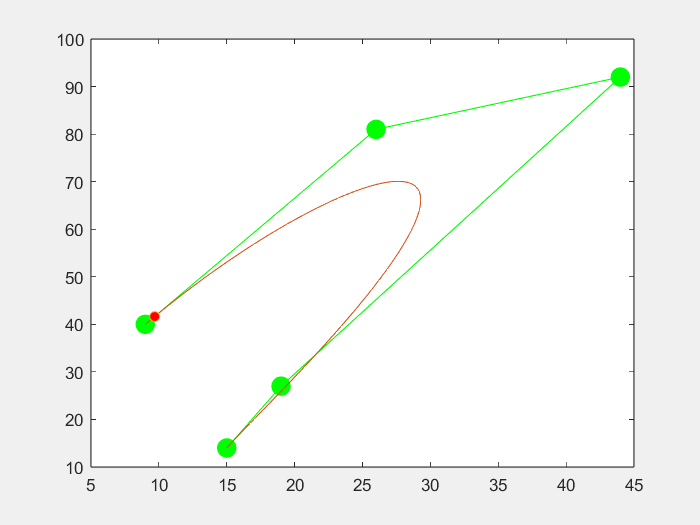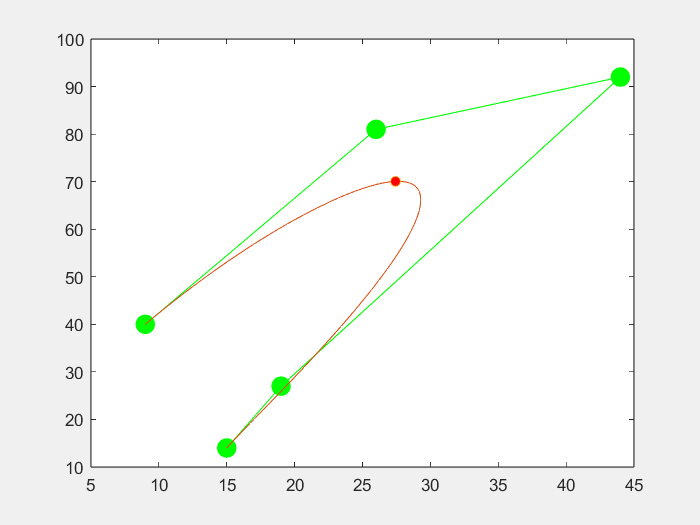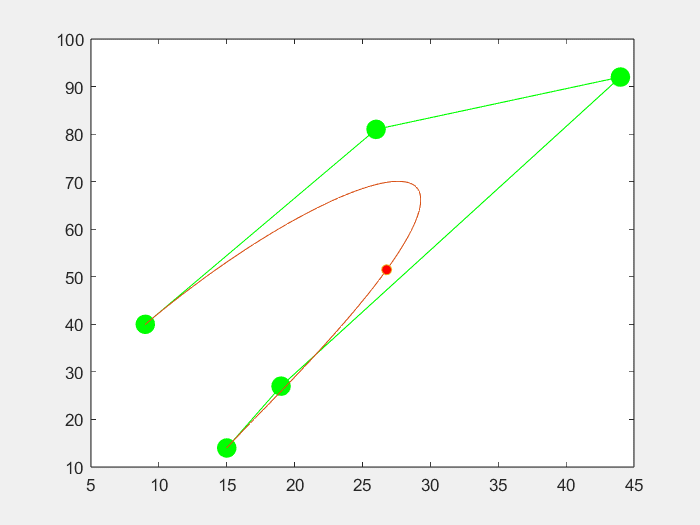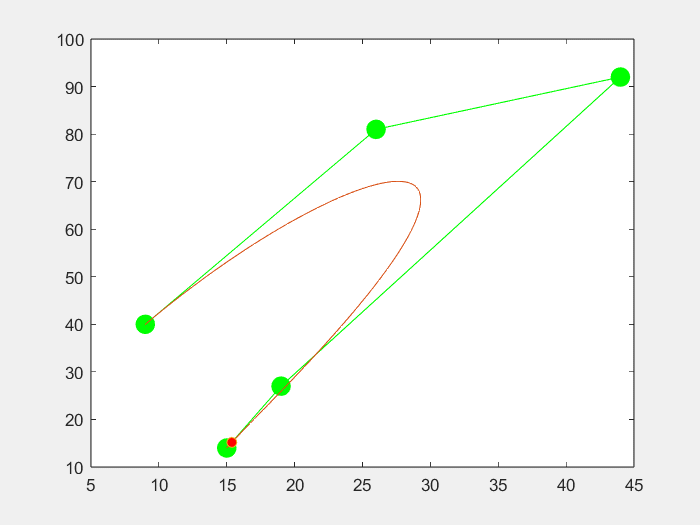
在这里插入图片描述

六个点
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1289785.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Leetcode每日一题学习训练——Python3版（最小化旅行的价格总和）

Leetcode每日一题学习训练——Python3版（最小化旅行的价格总和）

版本说明 当前版本号[20231206]。 版本修改说明20231206初版 目录 文章目录 版本说明目录最小化旅行的价格总和理解题目代码思路参考代码 原题可以点击此 2646. 最小化旅行的价格总和 前去练习。 最小化旅行的价格总和 现有一棵无向、无根的树&#xff0c;树中有 n 个节点…
阅读更多...
LeetCode Hot100 207.课程表

LeetCode Hot100 207.课程表

题目&#xff1a; 你这个学期必须选修 numCourses 门课程&#xff0c;记为 0 到 numCourses - 1 。 在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出&#xff0c;其中 prerequisites[i] [ai, bi] &#xff0c;表示如果要学习课程 ai 则 必须 先学习…
阅读更多...
人工智能在警务工作中的运用

人工智能在警务工作中的运用

AI 能否帮助警察打击犯罪&#xff1f; 执法部门负责维护公共安全&#xff0c;他们必须处理随之而来的所有挑战。幸运的是&#xff0c;警察可以依靠技术来处理很多工作。近几年来&#xff0c;尤其是人工智能技术在全球变成了警务工作中的一个重要部分。 随着基于 AI 的警务技术…
阅读更多...
如何在Java中实现多条件排序

如何在Java中实现多条件排序

文章目录 前言一、在Java中使用Comparator接口实现多条件排序二、视频讲解总结 前言 多条件排序是一个复杂而实用的技术问题&#xff0c;它涉及到算法、数据结构等多个领域。 在实际工作中&#xff0c;我们常常需要根据多个条件对数据进行排序&#xff0c;以达到最优化的效果。…
阅读更多...
桶排序去重

桶排序去重

题目&#xff1a; #include<stdio.h> int main() { int a[1001], n, i, t; for (i 1;i < 1000;i) { a[i] 0;//初始化 } scanf("%d", &n);//读入n for (i 1;i < n;i)//循环读入n个图书的ISBN号 { scanf(&…
阅读更多...
ABAP 字符串空白值保留长度或者用其他字符替代

ABAP 字符串空白值保留长度或者用其他字符替代

保留空白值在字符串的长度。 DATA lv_char1 TYPE string VALUE Hello. DATA lv_char2 TYPE string VALUE World. DATA LV_CHAR3 TYPE C LENGTH 50.DATA(lv_string3) |{ lv_char1 } { lv_char2 }!|.WRITE: / lv_string3.DATA(lv_string2) lv_char1 && | { lv_char3 } …
阅读更多...
分库分表详解

分库分表详解

分库分表很常见&#xff0c;但这些问题90%的人都答不全 分库分表&#xff0c;是企业里面比较常见的针对高并发、数据量大的场景下的一种技术优化方案&#xff0c;也是一个非常高频的面试题。但是&#xff0c;因为很多人其实并没有非常丰富的分库分表的经验&#xff0c;所以能把…
阅读更多...
虚拟线程原理及性能分析

虚拟线程原理及性能分析

一、背景 JDK21 在 9 月 19 号正式发布&#xff0c;带来了较多亮点&#xff0c;其中虚拟线程备受瞩目&#xff0c;毫不夸张的说&#xff0c;它改变了高吞吐代码的编写方式&#xff0c;只需要小小的变动就可以让目前的 IO 密集型程序的吞吐量得到提升&#xff0c;写出高吞吐量的…
阅读更多...
甘草书店：#8 2023年11月22日 星期三「“说一套做一套”的甘草与麦田」

甘草书店：#8 2023年11月22日 星期三「“说一套做一套”的甘草与麦田」

最近与甘草书店的投资方和意向投资方沟通&#xff0c;听取了来自不同领域不同人群的观点。他们讲的都有道理&#xff0c;但他们说的都不是甘草。就像“麦田”成立之前&#xff0c;世间没有“麦田”一样&#xff1b;“甘草”出现之前&#xff0c;世间没有也没有“甘草”。 故事…
阅读更多...
UDP多人群聊

UDP多人群聊

一&#xff0c;创建类 二&#xff0c;类 1&#xff0c;Liao类 import java.awt.*; import java.awt.event.*; import javax.swing.*; import java.net.*; import java.io.IOException; import java.lang.String; public class Liao extends JFrame{ private static fi…
阅读更多...
智慧景区（园区）数字孪生可视化GIS解决方案

智慧景区（园区）数字孪生可视化GIS解决方案

随着技术的日新月异&#xff0c;景区日常管理及运营中使用到的智慧化工具越来越丰富&#xff0c;智慧化硬件设备也越来越多&#xff0c;而其中各个管理系统往往又是相互独立&#xff0c;形成一个个数据孤岛。智慧景区管理平台就是将各个孤岛中的数据及功能汇集起来&#xff0c;…
阅读更多...
【数据结构】动态规划（Dynamic Programming）

【数据结构】动态规划（Dynamic Programming）

一.动态规划&#xff08;DP&#xff09;的定义&#xff1a; 求解决策过程&#xff08;decision process&#xff09;最优化的数学方法。 将多阶段决策过程转化为一系列单阶段问题&#xff0c;利用各阶段之间的关系&#xff0c;逐个求解。 二.动态规划的基本思想&#xff1a; …
阅读更多...
Kubernetes常用工作负载控制器

Kubernetes常用工作负载控制器

文章目录 一、常用负载控制器是什么二、Deployment控制器1.介绍2.使用流程3.应用部署4.应用升级5.滚动升级实现原理&#xff08;replicaset控制器&#xff09;6.滚动升级实现流程7.滚动升级策略8.应用实例扩容和缩容9.应用发布失败回滚10.应用下线 三、DaemonSet控制器四、Job控…
阅读更多...
elk+kafka+filebeat

elk+kafka+filebeat

elk1 cd /opt 把filebeat投进去 tar -xf filebeat-6.7.2-linux-x86_64.tar.gz mv filebeat-6.7.2-linux-x86_64 filebeat cd filebeat/ yum -y install nginx systemctl restart nginx vim /usr/share/nginx/html/index.html this is nginx cp filebeat.yml filebeat.yml.…
阅读更多...
在Vivado 仿真器中搭建UVM验证环境（不需要联合modelsim）

在Vivado 仿真器中搭建UVM验证环境（不需要联合modelsim）

Vivado 集成设计环境支持将通用验证方法学 (UVM) 应用于 Vivado 仿真器。Vivado 提供了预编译的 UVM V1.2 库。 &#xff08;1&#xff09;在 Vivado 2019.2 中创建新 RTL 工程。 &#xff08;2&#xff09;单击“添加目录 (Add Directories)”以将“src”和“verif”目录添加…
阅读更多...
LLM大语言模型（一）：ChatGLM3-6B本地部署

LLM大语言模型（一）：ChatGLM3-6B本地部署

目录 前言 本机环境 ChatGLM3代码库下载 模型文件下载 修改为从本地模型文件启动 启动模型网页版对话demo 超参数设置 GPU资源使用情况 &#xff08;网页对话非常流畅&#xff09; 前言 LLM大语言模型工程化&#xff0c;在本地搭建一套开源的LLM&#xff0c;方便后续的…
阅读更多...
Python实现FA萤火虫优化算法优化LightGBM分类模型(LGBMClassifier算法)项目实战

Python实现FA萤火虫优化算法优化LightGBM分类模型(LGBMClassifier算法)项目实战

说明&#xff1a;这是一个机器学习实战项目&#xff08;附带数据代码文档视频讲解&#xff09;&#xff0c;如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 萤火虫算法&#xff08;Fire-fly algorithm&#xff0c;FA&#xff09;由剑桥大学Yang于2009年提出 , …
阅读更多...
空间金字塔池化（SPP，Spatial Pyramid Pooling)系列

空间金字塔池化（SPP，Spatial Pyramid Pooling)系列

空间金字塔池化的作用是解决输入图片大小不一造成的缺陷&#xff0c;同时在目标识别中增加了精度。空间金字塔池化可以使得任意大小的特征图都能够转换成固定大小的特征向量&#xff0c;下面针对一些典型的空间金字塔进行盘点。 部分图片来自blog:空间金字塔池化改进 SPP / SP…
阅读更多...
第二十一章总结

第二十一章总结

一、网络通信&#xff1a; 1.网络程序设计基础&#xff1a;网络程序设计编写的是与其他计算机进行通信的程序。 1.1局域网与互联网&#xff1a;为了实现两台计算机的通信&#xff0c;必须用一个网络线路连接两台计算机 2.网络协议&#xff1a;网络协议规定了计算机之间连接的…
阅读更多...
【精选】WebLogic-CVE-2017-3506

【精选】WebLogic-CVE-2017-3506

下载地址&#xff1a; https://github.com/Al1ex/CVE-2017-3506https://github.com/Al1ex/CVE-2017-3506 1.weblogic wls-wsat组件远程命令执行&#xff08;CVE-2017-3506&#xff09; 复现&#xff1a; ┌──(root&#x1f480;kali)-[~/routing/红日2/CVE-2017-3506-mai…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023