版本说明

当前版本号[20231206]。

版本	修改说明
20231206	初版

目录

原题可以点击此 2646. 最小化旅行的价格总和 前去练习。

最小化旅行的价格总和

现有一棵无向、无根的树，树中有 n 个节点，按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。

每个节点都关联一个价格。给你一个整数数组 price ，其中 price[i] 是第 i 个节点的价格。

给定路径的 价格总和 是该路径上所有节点的价格之和。

另给你一个二维整数数组 trips ，其中 trips[i] = [starti, endi] 表示您从节点 starti 开始第 i 次旅行，并通过任何你喜欢的路径前往节点 endi 。

在执行第一次旅行之前，你可以选择一些 非相邻节点 并将价格减半。

返回执行所有旅行的最小价格总和。

示例 1：

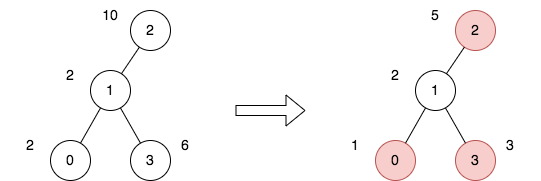
输入：n = 4, edges = [[0,1],[1,2],[1,3]], price = [2,2,10,6], trips = [[0,3],[2,1],[2,3]]
输出：23
解释：
上图表示将节点 2 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 、2 和 3 并使其价格减半后的树。
第 1 次旅行，选择路径 [0,1,3] 。路径的价格总和为 1 + 2 + 3 = 6 。
第 2 次旅行，选择路径 [2,1] 。路径的价格总和为 2 + 5 = 7 。
第 3 次旅行，选择路径 [2,1,3] 。路径的价格总和为 5 + 2 + 3 = 10 。
所有旅行的价格总和为 6 + 7 + 10 = 23 。可以证明，23 是可以实现的最小答案。

示例 2：

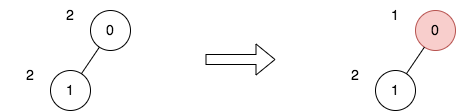
输入：n = 2, edges = [[0,1]], price = [2,2], trips = [[0,0]]
输出：1
解释：
上图表示将节点 0 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 并使其价格减半后的树。 
第 1 次旅行，选择路径 [0] 。路径的价格总和为 1 。 
所有旅行的价格总和为 1 。可以证明，1 是可以实现的最小答案。

提示：

• 1 <= n <= 50
• edges.length == n - 1
• 0 <= ai, bi <= n - 1
• edges 表示一棵有效的树
• price.length == n
• price[i] 是一个偶数
• 1 <= price[i] <= 1000
• 1 <= trips.length <= 100
• 0 <= starti, endi <= n - 1

理解题目

首先需要构建一棵树，然后使用动态规划来计算每个节点作为根节点时的最小价格总和。

在计算过程中，可以选择一些非相邻节点并将价格减半。

简单来说就是：

1. 构建树结构
2. 初始化动态规划数组
3. 遍历所有旅行，计算每个节点作为根节点时的最小价格总和
4. 返回最小价格总和

代码思路

1. 首先，根据给定的边信息构建一个邻接表来表示树结构。每个节点都有一个子节点列表，用于存储与该节点相连的其他节点。

   def minimumTotalPrice(self, n: int, edges: List[List[int]], price: List[int], trips: List[List[int]]) -> int:
           # 构建邻接表表示树结构
           children = [[] for _ in range(n)]
           for edge in edges:
               children[edge[0]].append(edge[1])
               children[edge[1]].append(edge[0])
   

2. 然后，初始化一个计数器数组 count，用于记录每个节点在行程中出现的次数。

     # 初始化每个节点的计数器
           count = [0] * n
   

3. 接下来，使用深度优先搜索（DFS）遍历树结构，计算从起点到终点的路径上的节点数量。在遍历过程中，如果到达终点节点，则将该节点的计数器加一。

    # 深度优先搜索，计算从起点到终点的路径上的节点数量
           def dfs(node: int, parent: int, end: int) -> bool:
               if node == end:
                   count[node] += 1
                   return True
               for child in children[node]:
                   if child == parent:
                       continue
                   if dfs(child, node, end):
                       count[node] += 1
                       return True
               return False
   

4. 遍历所有行程，对于每个行程的起点和终点，调用 DFS 函数来计算从起点到终点的路径上的节点数量，并将结果累加到对应节点的计数器中。

   # 遍历所有行程，计算每个节点在行程中出现的次数
           for [x, y] in trips:
               dfs(x, -1, y)
   

5. 最后，使用动态规划（DP）来计算每个节点作为根节点时的最小总价格。在 DP 函数中，首先计算当前节点作为根节点时的总价格，然后递归地计算其子节点作为根节点时的最小总价格，并根据题目要求进行选择。

     # 动态规划，计算每个节点作为根节点时的最小总价格
           def dp(node: int, parent: int) -> List[int]:
               res = [
                   price[node] * count[node], price[node] * count[node] // 2
               ]
               for child in children[node]:
                   if child == parent:
                       continue
                   [x, y] = dp(child, node)
                   # node 没有减半，因此可以取子树的两种情况的最小值
                   # node 减半，只能取子树没有减半的情况
                   res[0], res[1] = res[0] + min(x, y), res[1] + x
               return res
   

6. 最终返回根节点为0时的最小总价格。

        # 返回根节点为0时的最小总价格
        return min(dp(0, -1))

参考代码

这段代码是一个解决旅行商问题（TSP）的算法，通过构建树结构、计算节点出现次数和使用动态规划来计算旅行商问题的最小总价格。

class Solution:
    def minimumTotalPrice(self, n: int, edges: List[List[int]], price: List[int], trips: List[List[int]]) -> int:
        children = [[] for _ in range(n)]
        for edge in edges:
            children[edge[0]].append(edge[1])
            children[edge[1]].append(edge[0])
        
        count = [0] * n
        def dfs(node: int, parent: int, end: int) -> bool:
            if node == end:
                count[node] += 1
                return True
            for child in children[node]:
                if child == parent:
                    continue
                if dfs(child, node, end):
                    count[node] += 1
                    return True
            return False
        
        for [x, y] in trips:
            dfs(x, -1, y)
        
        def dp(node: int, parent: int) -> List[int]:
            res = [
                price[node] * count[node], price[node] * count[node] // 2
            ]
            for child in children[node]:
                if child == parent:
                    continue
                [x, y] = dp(child, node)
                # node 没有减半，因此可以取子树的两种情况的最小值
                # node 减半，只能取子树没有减半的情况
                res[0], res[1] = res[0] + min(x, y), res[1] + x
            return res

        return min(dp(0, -1))