一、题目内容

二、思路分析

这道题也是一个很经典的DP问题。

再次之前我们先回顾一下之前所写的DP文章的解析。我们都是用$i-1$的规模的子问题来求解我们当前的问题。

其实，有一点类似于贪心的感觉，就是我们不断地做对当下最好的选择。

比如我们之前的背包问题、子序列问题，我们都是看的最后一个元素，我们只做出当下最好的选择，而体现出我们做最好选择的部分就是我们通过比较选出最大值最小值的代码。

但是这道题不一样，这道题将带给我们新的理解。

如果说我们之前的问题是贪心+DP，那么我们今天的问题就是分治+贪心+DP。

其中DP决定了我们这道题的框架，而前面的算法决定了我们书写状态转移方程的依据。

1、状态转移方程

（1）状态表示

状态表示通常来源于问题，问题中的变量通常代表了状态的规模。

我们这道题用$f(i,j)$来表示合并区间$[i,j]$的石子所需要的最少的代价。

（2）状态转移

状态转移我们这里要使用分治的思想。

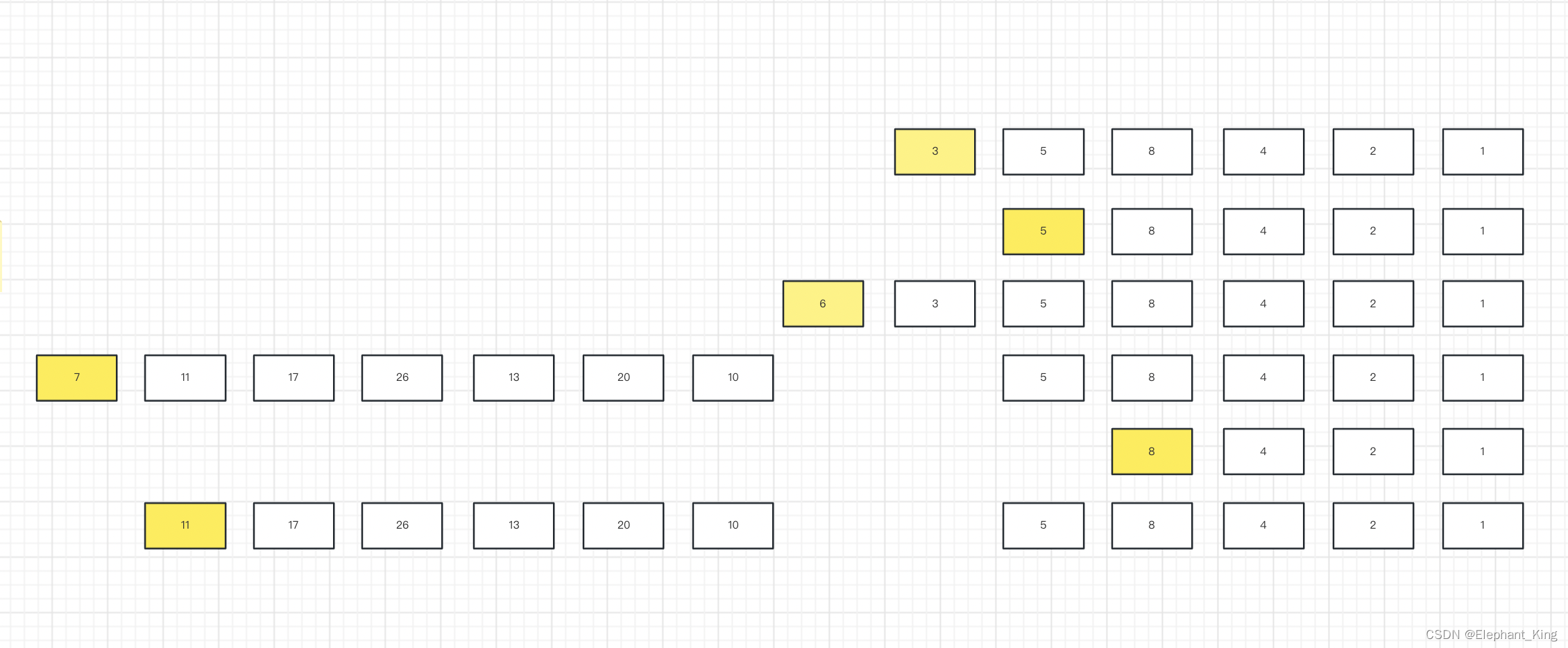
这里使用的分治类似于我们的快速排序。

如下图所示：

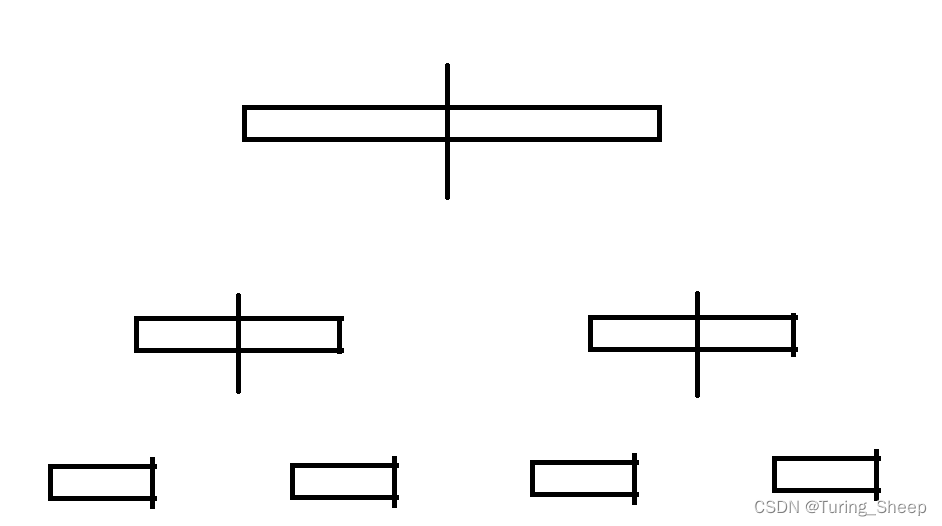
图中的黑线表示合并两大堆石子的最优选择。

那么我们怎么知道这个黑线的位置呢？我们只需要去枚举比较出最优即可。

当我们做出了最优选择后，我们需要对每一小堆做同样的操作。

接下来我们就可以去写一下状态方程的表示了：

$$f(i,j)=max(f(i,k)+f(k+1,j)+S[i][j],f(i,j))$$
我们来解释一下，这个$k$就是我们所有可能合并两堆石子的位置。

我们合并两堆石子，必定需要加上两堆的石子数目作为代价。即我们的$S[i][j]$。

2、循环设计及初始化

（1）循环

循环一定是从最小的子问题开始的，我们最小的子问题就是合并真正意义上的两堆石子，即区间长度是2。因此，我们要枚举出所有可能合并的情况。

那么我们的外循环$i$负责区间的长度，内循环负责所有区间长度为$i$的情况，并计算出代价。

（2）初始化

初始化从现在开始是一个非常重要的环节，之前的背包问题等好多问题也涉及到了初始化的问题，但是由于我们的 f 数组是全局变量，因此就都初始化为0，而那些问题恰好也是初始化为0的。所以我们就没有提。

今天的问题或许也是初始化为0，但是我们需要注意一下初始化的问题，那么涉及到初始化的一定是最小的子问题。

我们发现，我们的最小问题的长度为2的子序列。那长度为1的呢？长度为1就说明我们就这一堆石子。我们无需花费任何代价，因此我们需要将所有的$f[1][j]$初始化为0。

但是由于全局变量的原因，我们可以不写，但是不写不代表我们不用思考初始化。

3、代码实现

由于最终我们会加上某段区间所有石子的代价，所以我们这里使用前缀和优化一下。

#include<iostream>
using namespace std;
const int N=310;
int f[N][N];
int s[N];
int n;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        int x;
        scanf("%d",&x);
        s[i]=x+s[i-1];
    }
    for(int i=2;i<=n;i++)
    {
        for(int j=1;j+i-1<=n;j++)
        {
            int l=j,r=j+i-1;
            f[l][r]=0x3f3f3f3f;
            for(int k=l;k<r;k++)
            {
                f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);
            }
        }
    }
    cout<<f[1][n]<<endl;
    return 0;
}