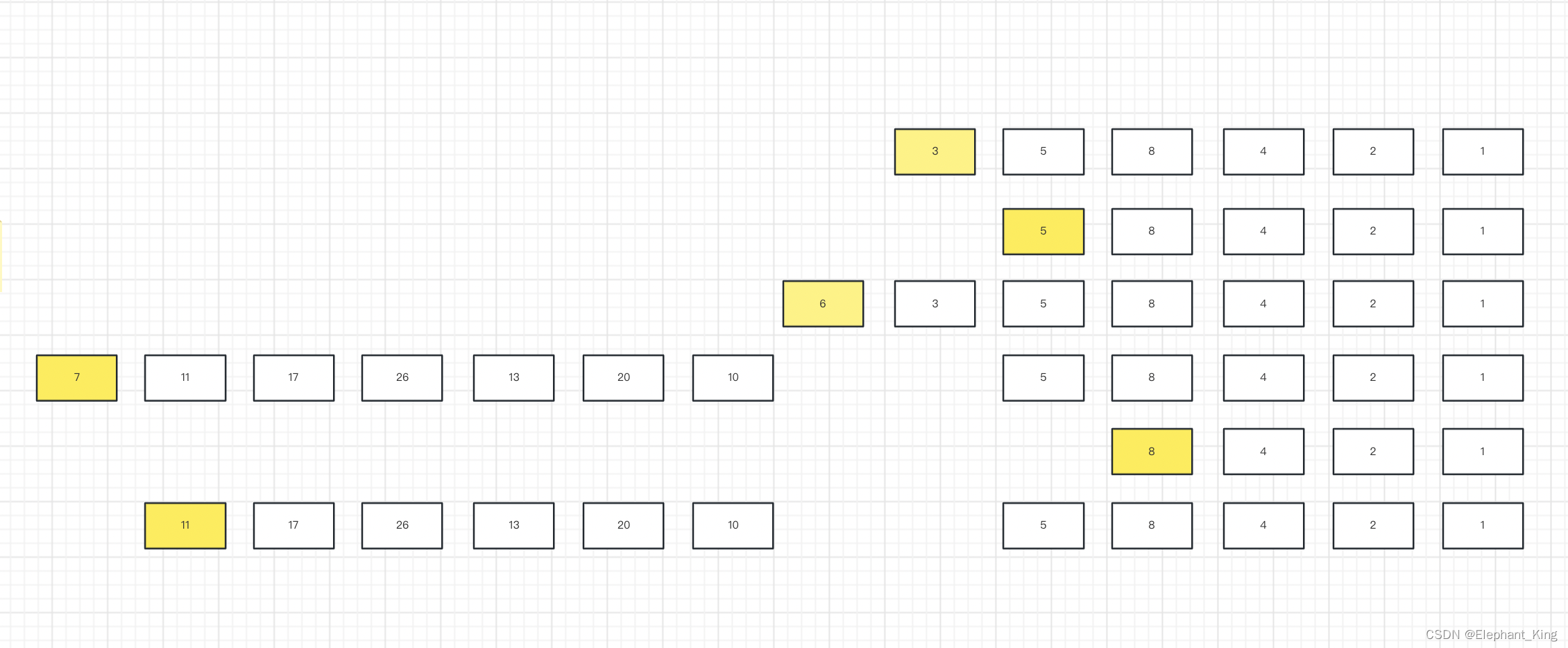
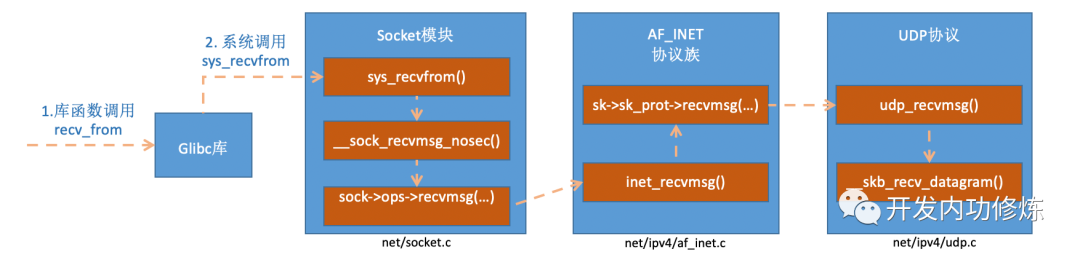
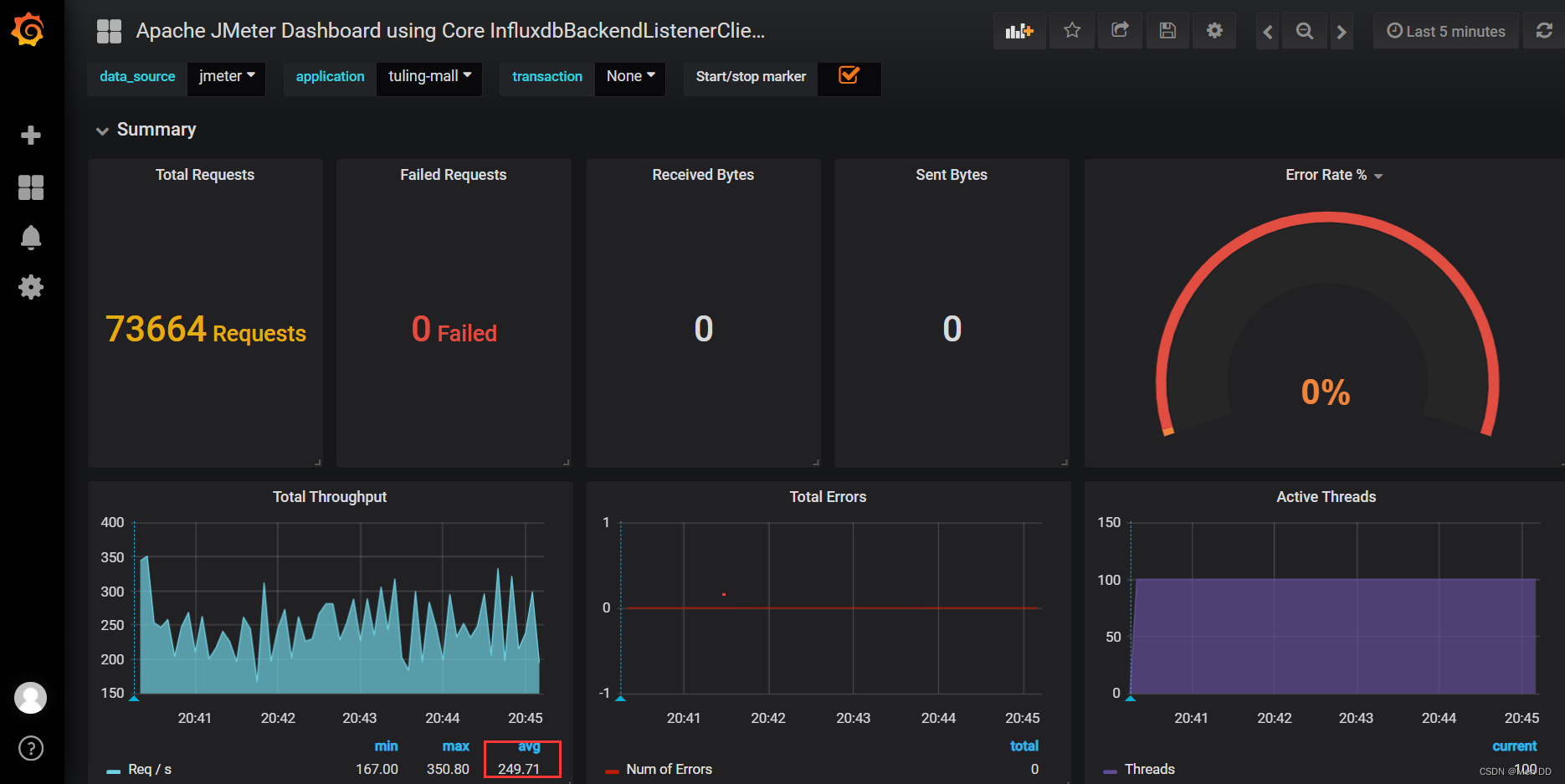
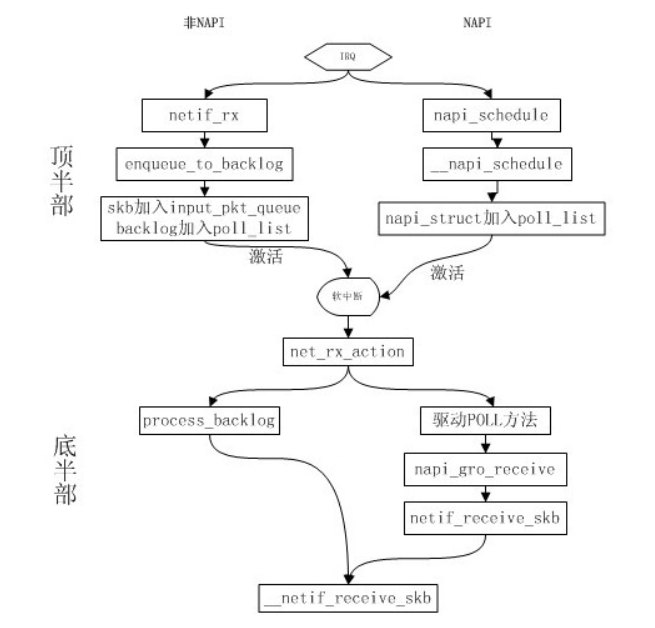
1、全局阈值算法

基于灰度直方图的优化迭代算法之一。

Iterative Scheduler and Modified Iterative Water-Filling
In the downlink, the inter-cell interference is only function of the power levels and is independent of the user scheduling decisions. This suggests that the user scheduling and the power allocation can be carried out separately. An iterative scheduler can be derived so that the best user to schedule are first found assuming a fixed power allocation, then the best power allocation are computed for the fixed scheduled users [VPW09, YKS10]. If the iteration always increases the objective function monotonically, one can guarantee the convergence of the scheduler to at least a local optimum.

2、全局阈值算法的源程序

using System;
using System.Linq;
using System.Text;
using System.Drawing;
using System.Collections;
using System.Collections.Generic;
using System.Runtime.InteropServices;
using System.Drawing.Imaging;

namespace Legalsoft.Truffer.ImageTools
{
    public static partial class BinarizationHelper
    {

        #region 灰度图像二值化 全局算法 全局阈值算法

        /// <summary>
        /// 基本全局阈值法
        /// https://blog.csdn.net/xw20084898/article/details/17564957
        /// </summary>
        /// <param name="histogram"></param>
        /// <returns></returns>
        private static int Basic_Global_Threshold(int[] histogram)
        {
            double t = Histogram_Sum(histogram);
            double u = Histogram_Sum(histogram, 1);
            int k2 = (int)(u / t);

            int k1;
            do
            {
                k1 = k2;
                double t1 = 0;
                double u1 = 0;
                for (int i = 0; i <= k1; i++)
                {
                    t1 += histogram[i];
                    u1 += i * histogram[i];
                }
                int t2 = (int)(t - t1);
                double u2 = u - u1;
                if (t1 != 0)
                {
                    u1 = u1 / t1;
                }
                else
                {
                    u1 = 0;
                }
                if (t2 != 0)
                {
                    u2 = u2 / t2;
                }
                else
                {
                    u2 = 0;
                }
                k2 = (int)((u1 + u2) / 2);
            } while (k1 != k2);

            return (k1);
        }

        public static void Global_Threshold_Algorithm(byte[,] data)
        {
            int[] histogram = Gray_Histogram(data);
            int threshold = Basic_Global_Threshold(histogram);
            Threshold_Algorithm(data, threshold);
        }

        #endregion

    }
}

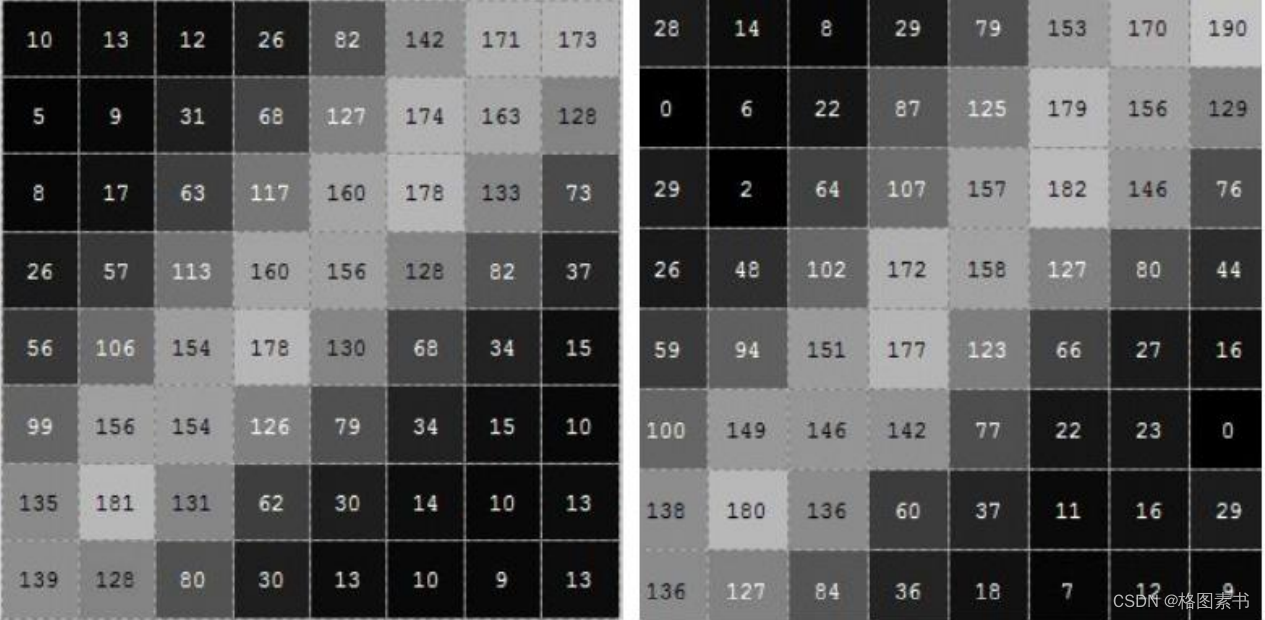
3、全局阈值算法的计算效果

The thematic series Iterative Methods and Optimization Algorithms is devoted to the latest achievements in the field of iterative methods and optimization theory for single-valued and multi-valued mappings. The series is related to the significant contributions in these fields of Professor Hong-Kun Xu, as well as to some important recent advances in theory, computation, and applications.

In this chapter we focus on general approach to optimization for multivariate functions. In the previous chapter, we have seen three different variants of gradient descent methods, namely, batch gradient descent, stochastic gradient descent, and mini-batch gradient descent. One of these methods is chosen depending on the amount of data and a trade-off between the accuracy of the parameter estimation and the amount time it takes to perform the estimation. We have noted earlier that the mini-batch gradient descent strikes a balance between the other two methods and hence commonly used in practice. However, this method comes with few challenges that need to be addressed. We also focus on these issues in this chapter.

Learning outcomes from this chapter:
Several first-order optimization methods
Basic second-order optimization methods

This chapter closely follows chapters 4 and 5 of (Kochenderfer and Wheeler 2019). There are many interesting textbooks on optimization, including (Boyd and Vandenberghe 2004), (Sundaram 1996), and (Nesterov 2004),