金字塔学习模型
金字塔学习是美国学习专家爱德加·戴尔1946年提出的。
他将学习分为主动学习和被动学习两种类型,用数字形象地呈现了采用不同学习方式,学习者在两周后还能记住的内容有多少。
- 被动学习:通过听讲、阅读、视听、演示这些活动,对学习内容的平均留存率为 5%、10%、20%和 30%。
- 主动学习:通过讨论、实践、教授给他人,将被动学习的内容留存率提升到 50%、75% 和 90%。
根据此模型,学习效果在 30%以下的都是个人学习和被动学习,而学习效果在 50%以上的都是团队学习,主动学习和参与式学习。
学习的最佳效果,就是要把学到的知识内化于心,外化于形。而这一点,恰好符合明朝思想家王守仁(王阳明)提出来的哲学理论—— 知行合一不谋而合。
知行合一,即认识事物的道理与行动起来,是密不可分的。知是指内心的觉知,对事物的认识,行是指人的实际行为。
善用学习金字塔模型第七层——教给他人,以教为学,知行合一,才能呈现绝佳的学习效果。

金字塔学习模型
费曼学习法
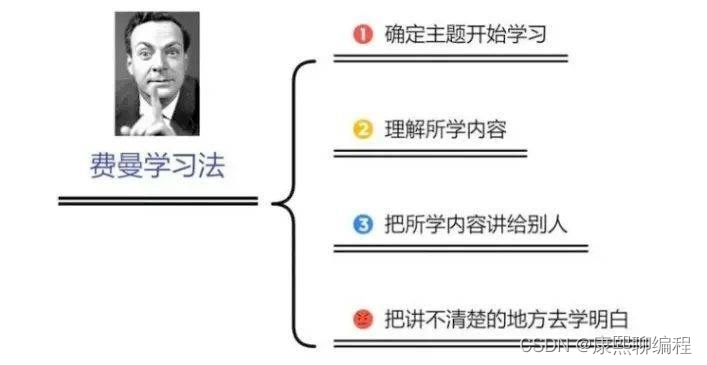
费曼学习法是由著名物理学家、诺贝尔物理学奖得主理 查德·费曼提出的。
其核心就是: 通过简短的语言,向别人清楚地解说一件事,来检验自己是否真的弄懂了这件事。
费曼学习法通过“以教促学”的方式让人在短时间内掌握知识,并且快速吸收信息。
在西汉·戴圣《礼记·学记》中写道:
是故学然后知不足, 教然后知困。 知不足然后能自反也, 知困然后能自强也。 故曰:‘教学相长’也。
说的是同样的道理。
费曼学习法
艾宾浩斯遗忘学习法
我们在学生时代的时候,应该都了解过艾宾浩斯遗忘曲线,尤其是在学英语的时候。
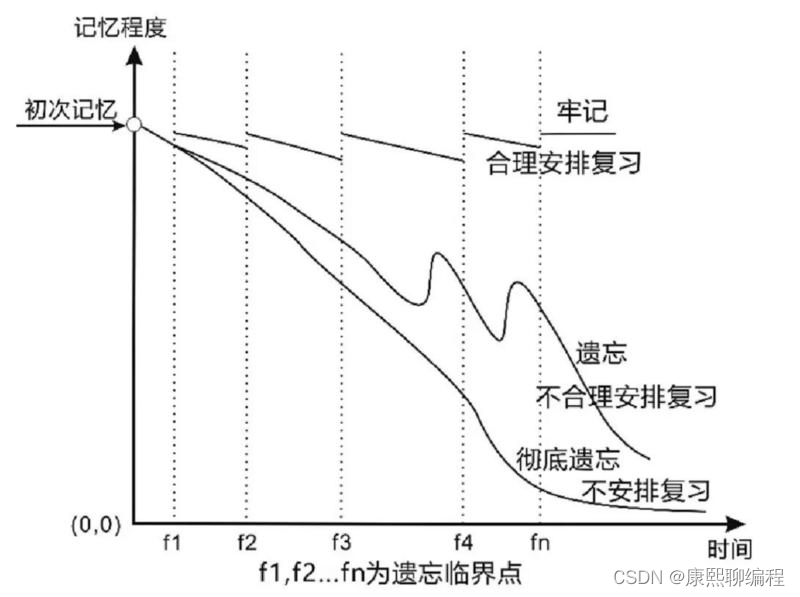
遗忘曲线(Forgetting curve)是用于表述记忆中的中长期记忆的遗忘率的一种曲线。这一曲线最早由心理学家赫尔曼·艾宾浩斯通过自己1880年到1885年的实验提出。在这一实验中,艾宾浩斯使用了一些毫无意义的字母组合。通过记忆这些字母组合,并在一系列时间间隔后检查遗忘率,得到了这一曲线。因此,这一曲线又叫艾宾浩斯遗忘曲线。
记忆的保持在时间上是不同的,有短期记忆和长期记忆两种。
平时的记忆的过程是:输入的信息在经过人的注意过程的学习后,便成为了人的短期的记忆,再经过进一步强化后成为长期记忆。长期记忆的保持时间有长有短,如果不经过及时的复习,这些记住过的东西就会遗忘,而经过了及时的复习,长期记忆就会继续保持下去。
那么,对于我们来讲,怎样才叫做遗忘呢,所谓遗忘就是我们对于曾经记忆过的东西不能再认起来,也不能回忆起来,或者是错误的再认和错误的回忆,这些都是遗忘。艾宾浩斯在做这个实验的时候是拿自己作为测试对象的,他得出了一些关于记忆的结论。他选用了一些根本没有意义的音节,也就是那些不能拼出单词来的众多字母的组合,比如“asww”、“cfhhj”、“ijikmb”、“rfyjbc”等等。他经过对自己的测试,得到了一些数据。
基于测试数据得出人脑的遗忘的进程并不是平均的,最初时大脑遗忘的速度很快,随后会逐渐缓慢,我们大脑的记忆曲线分为 8 个周期,5分钟、半小时、12小时、1天、2天、4天、7天、15天,这个方法提倡的是重复温习,减少遗忘,重复记忆的频次是核心,因此只要我们掌握正确的时间点进行复习就会事半功倍。
子曰:“学而时习之,不亦说(yuè)乎?” -- 语出《论语·学而》
释义:学习后经常用所学的知识经常复习,不是很愉快吗?
艾宾浩斯遗忘曲线
刻意练习法
著名心理学家艾利克森和他的同事曾经开展过一项关于锻炼记忆力的实验,邀请一个普通的大学生史蒂夫尝试记忆一串随意无序的数字。最初,他像普通人一样,只能记住8个左右,经过练习,慢慢地突破 9 个、10 个……,最终, 他的成绩达到了不可思议的一次记下 82 个无序数字串。
刻意练习法是利用人脑的习惯特征去学习和记忆,当我们在学习时,通过反复且频繁的刺激大脑中的神经突触,长久下来之后脑细胞会逐渐被激活且变得活跃,当这个学习行为发生的频率足够多时,就会逐渐进入我们行为的习惯区域,大脑能感知的用途变得足够多,遇到熟悉的行为时,大脑会走捷径下意识的做出反应,快速支撑学习需求。
番茄工作法
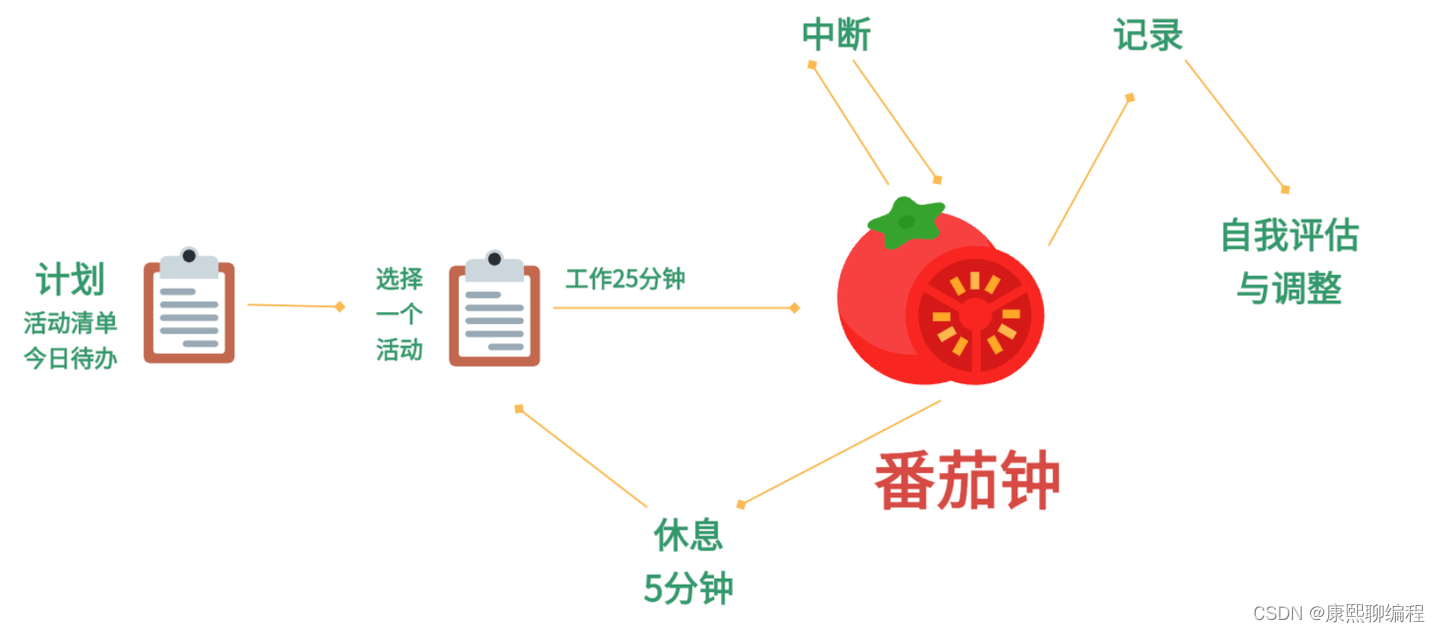
番茄工作法(英语:Pomodoro Technique)是一种时间管理方法,在 1980 年代由意大利学者 Francesco Cirillo 创立。该方法使用一个定时器来分割出一个一般为25分钟的工作时间和5分钟的休息时间,而那些时间段被称为pomodoros,为意大利语单词 pomodoro(中文:番茄)。
番茄工作法有五个步骤:
1. 决定需要完成的任务 2. 设定番茄工作法定时器至 n 分钟(通常为25分钟) 3. 持续工作直至定时器提示,记下一个番茄 4. 短暂休息3-5分钟 5. 每四个番茄,休息15-30分
番茄工作法的关键是规划,追踪,记录,处理,以及可视化。
在规划阶段,根据优先级将任务排入 To Do List。 预估每个任务的工作量。当每个番茄时结束后,成果会被记录下来,以提高参与者的成就感,并为未来的自我观察和改进提供原始数据。
番茄工作法的本质目的是减少内生和外在的干扰对意识流的影响。
一个单位的番茄工作时不可再细分。当在番茄工作时中被打断的情况下,必须重新开始。
番茄工作法
西蒙学习法
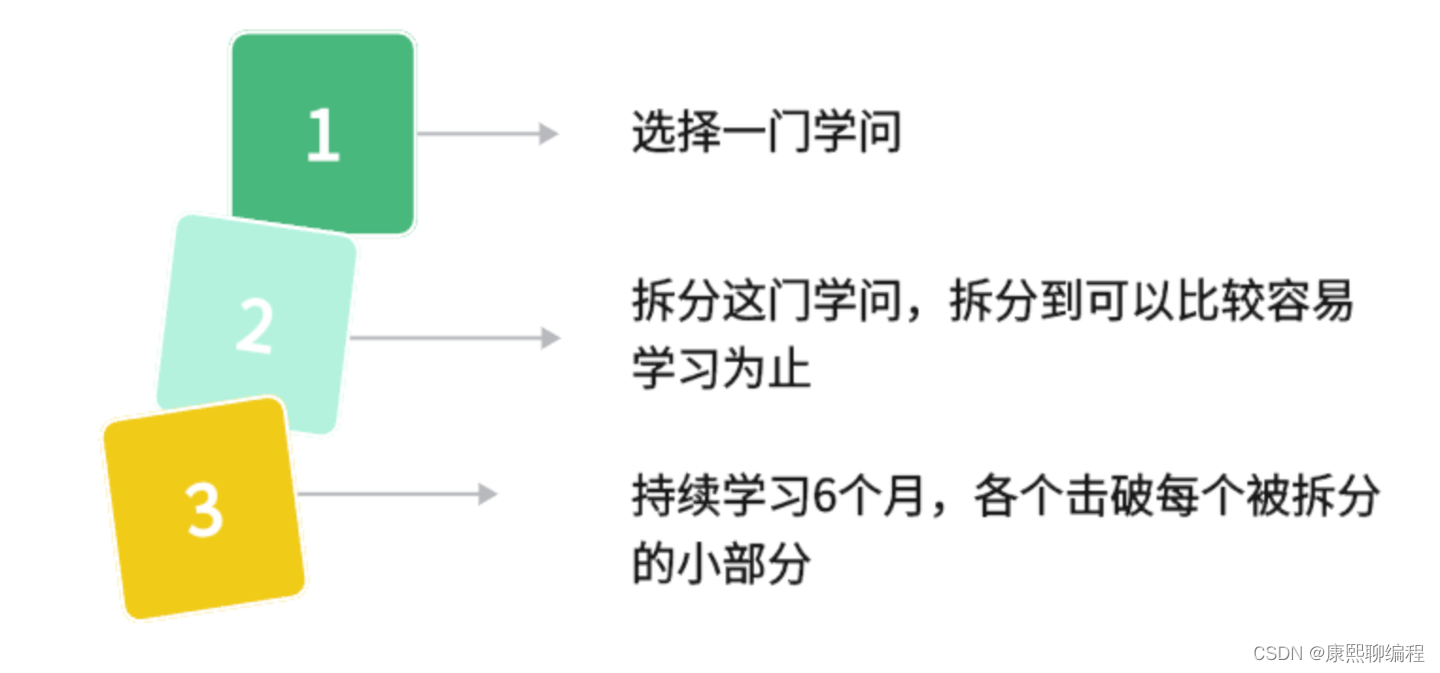
赫伯特·西蒙(HerbertA.Simon),1978年诺贝尔经济学奖获得者,1975年图灵奖获得者。他提出的一个理论:“对于一个有一定基础的人来说,只要真正肯下功夫,在 6 个月内就可以掌握任何一门学问。”西蒙学习法使用的原理是集中力量将知识分而治之。
人们常把西蒙学习法比作一把锥子或凿子。
锤子的打击力类比于能力,石头类比于知识,锥尖类比于精力的聚焦程度,连续敲击就像连续学习的时间。锤子的打击力越大,那么石头越容易被拆分,从而各个击破;锥尖越尖,锥子越容易插入石头,从而拆分石头;时间越长,则在石头上的凿痕越深,越容易拆分这块石头。
集中时间学习一门学问或知识,可以减少由一种学问到另一种学问的时间损失;可以减少回忆所需时间和加快进入这门学问的速度;理解度的增加使得后期的学习速度加快。
这种“锥形学习法”的高效原理在于,连续的长时间学习本身包含对之前学习内容的应用,这样就省去了大量的复习时间。
西蒙学习法认为,解决问题包括两大方法,分别是降低问题难度和提高能力。降低问题难度有 4 种常用的方法,包括拆分(分而治之)、类比、联想和追本溯源。提高能力有 2 种方法,包括广义动量定理和系统思考。简单来说,实际操作时可以分成以下3个步骤。
1. 选择学习领域,设定任务目标 2. 拆分学习内容 3. 集中精力学习
西蒙学习法
斯科特·扬学习法
斯科特·扬在家用了 12 个月时间,通过互联网,完成了麻省理工学院大学四年 33 门的计算机课程。之后,周游各国,一年学会了四国语言。
斯科特·扬提出整体学习性的学习方法,提倡人们不再有“工具人”的思维,而是要采取整体性学习。
知识点之间是互相联系的,而不是单一的,因此整体性学习意味着知识的学习并不是孤立的,而是运用大脑里已有的知识,对信息进行整合,将知识联系起来以达到记忆和应用知识的目的,这种学习方法主要有以下五个方面。
1. 获取:通过感官获取信息 2. 理解:明白信息的表面含义 3. 拓展:与其他信息建立联系 4. 纠错:纠正错误的地方 5. 应用:把知识应用到生活中的各种场景
斯科特·扬在他的著作《如何高效学习》中,介绍了整体性学习方法,非常值得一看。

斯科特扬学习法