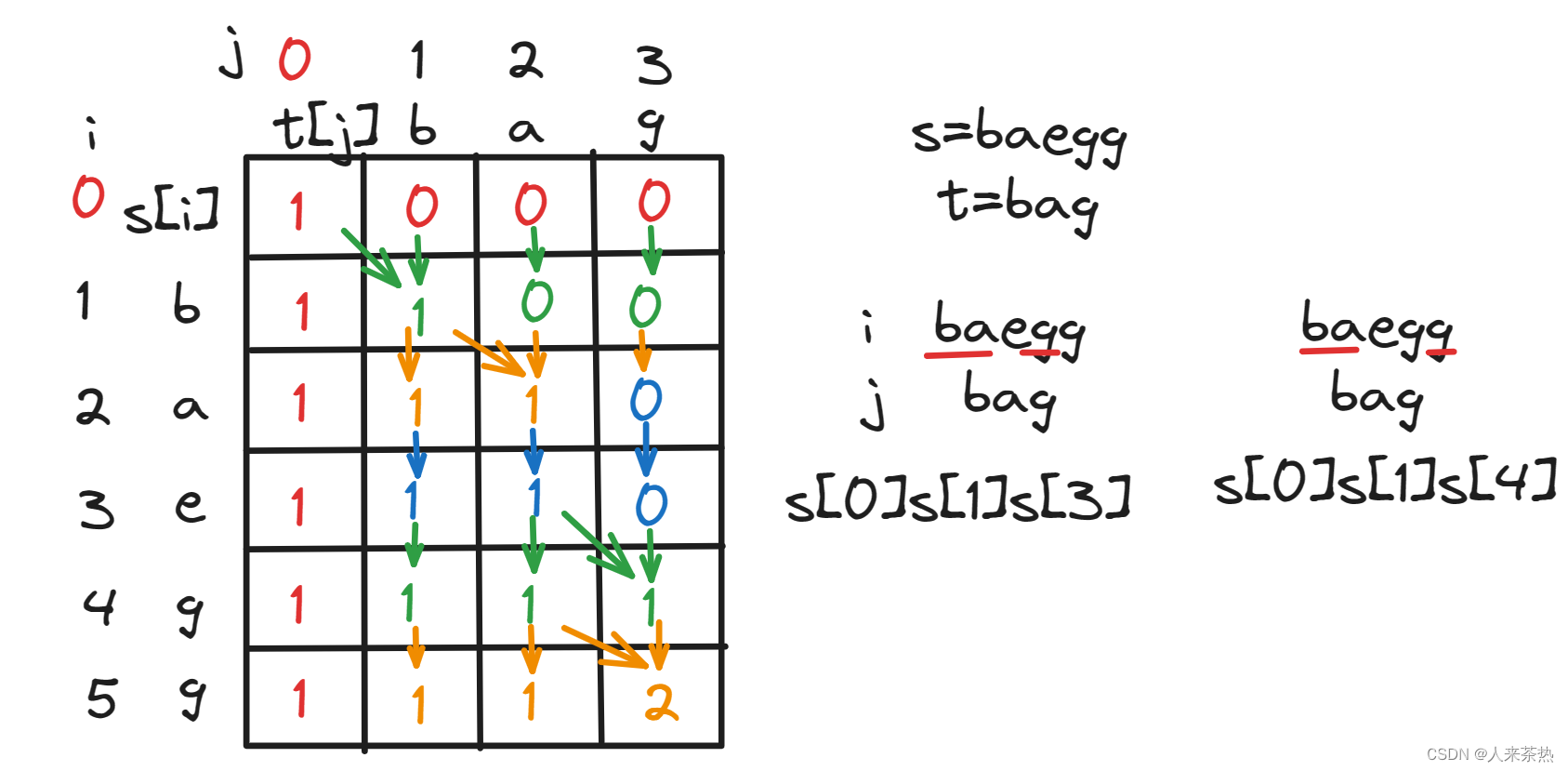
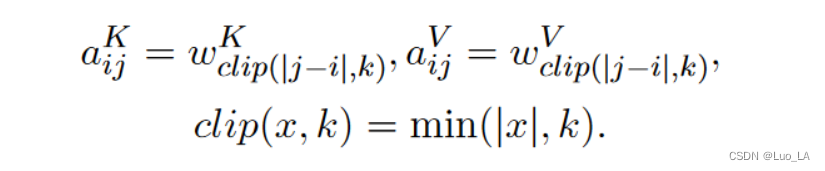描述
复数E包含实部x和虚部y, E=x+yi;E的模为:
输入n(<=1000)和n对(x,y);
按模数升序对复合体进行排序,如果模数相等,则按输入顺序排序。
排序后输出n行of (x_i,y_i,mod_i),保留2个十进制小数。
输入
输入n和n对(x,y);
输出
输出排序后的n行(x,y,mod)。
样例输入
3
2 2
1 1
3 3样例输出
1.00 1.00 1.41
2.00 2.00 2.83
3.00 3.00 4.24code1(给struct取小名
#include<stdio.h>
#include<math.h>
#include<stdlib.h>
typedef struct{
double x;
double y;
double mo;
int index;
}Complexnum;
int cmp(const void*a,const void *b){
const Complexnum *num1=(const Complexnum*)a;
const Complexnum *num2=(const Complexnum*)b;
if(num1->mo>num2->mo) return 1;
if(num1->mo<num2->mo) return -1;
if(num1->index>num2->index) return 1;
if(num1->index<num2->index) return -1;
return 0;
}
int main(){
int n;
while(scanf("%d",&n)!=EOF){
Complexnum *complexnum=(Complexnum *)malloc(n*sizeof(Complexnum));
for(int i=0;i<n;i++){
scanf("%lf%lf",&complexnum[i].x,&complexnum[i].y);
double mo1=sqrt(complexnum[i].x*complexnum[i].x+complexnum[i].y*complexnum[i].y);
complexnum[i].mo=mo1;
complexnum[i].index=i;
}
qsort(complexnum,n,sizeof(Complexnum),cmp);
for(int i=0;i<n;i++){
printf("%.2lf %.2lf %.2lf\n",complexnum[i].x,complexnum[i].y,complexnum[i].mo);
}
free(complexnum);
}
return 0;
}code2(不给struct取小名)
#include<stdio.h>
#include<math.h>
#include<stdlib.h>
typedef struct{
double x;
double y;
double mo;
int index;
}Complexnum;
int cmp(const void*a,const void *b){
const Complexnum *num1=(const Complexnum*)a;
const Complexnum *num2=(const Complexnum*)b;
if(num1->mo>num2->mo) return 1;
if(num1->mo<num2->mo) return -1;
if(num1->index>num2->index) return 1;
if(num1->index<num2->index) return -1;
return 0;
}
int main(){
int n;
while(scanf("%d",&n)!=EOF){
Complexnum *complexnum=(Complexnum *)malloc(n*sizeof(Complexnum));
for(int i=0;i<n;i++){
scanf("%lf%lf",&complexnum[i].x,&complexnum[i].y);
double mo1=sqrt(complexnum[i].x*complexnum[i].x+complexnum[i].y*complexnum[i].y);
complexnum[i].mo=mo1;
complexnum[i].index=i;
}
qsort(complexnum,n,sizeof(Complexnum),cmp);
for(int i=0;i<n;i++){
printf("%.2lf %.2lf %.2lf\n",complexnum[i].x,complexnum[i].y,complexnum[i].mo);
}
free(complexnum);
}
return 0;
}





![随机链表的复制[中等]](https://img-blog.csdnimg.cn/direct/cf962e1010e24cc7a54fcefb73c99443.png)