题目1:392 判断子序列
题目链接:判断子序列
对题目的理解
判断字符串s是否为t的子序列
字符串s和字符串t的长度大于等于0,字符串s的长度小于等于字符串t的长度,本题其实和最长公共子序列的那道题很相似,相当于找两个子序列的最长公共序列长度,最终这个最长公共序列的长度是否等于字符串s的长度
进阶:如果有大量的字符串s,s1,s2,....,sk(k>=10亿),依次检查是否为t的子序列
动态规划(编辑距离的入门题目)
动规五部曲
1)dp数组及下标i的含义
dp[i][j]:以i-1为结尾的字符串s和以j-1为结尾的字符串t的最长公共子序列的长度
2)递推公式

if (s[i - 1] != t[j - 1]),此时相当于t要删除元素,如果把当前元素t[j - 1]删除,那么dp[i][j] 的数值就是 看s[i - 1]与 t[j - 2]的比较结果了,即:dp[i][j] = dp[i][j - 1];
3)dp数组初始化
根据dp数组的定义,dp[i][0],dp[0][j]没有意义,但是为了满足递推公式,将其初始化为0,其余下标初始化为任意值均可,在之后的计算会被新值覆盖,但是为了初始化方便,均初始成0
4)遍历顺序
根据递推公式,dp[i][j]由dp[i-1][j-1]和dp[i][j-1]推出,遍历顺序从上到下,从左到右

5)打印dp数组
最终的输出结果是dp[s.size()][t.size()]代表最长相同子序列的长度,因为一定要将字符串s和字符串t遍历完,才能判断字符串是否为字符串s的子序列,要不放过任何一个字符,这样才能确保完整性,不落掉任意一个字符,如果这个长度等于s.size(),说明s是t的子序列,返回true
代码,可以直接使用最长公共子序列的代码,只是在最终返回结果的时候与s.size()比较一下
class Solution {
public:
bool isSubsequence(string s, string t) {
//定义并初始化dp数组
vector<vector<int>> dp(s.size()+1,vector<int>(t.size()+1,0));
for(int i=1;i<=s.size();i++){
for(int j=1;j<=t.size();j++){
if(s[i-1]==t[j-1]) dp[i][j]=dp[i-1][j-1]+1;
else dp[i][j]=max(dp[i][j-1],dp[i-1][j]);
}
}
if(dp[s.size()][t.size()]==s.size()) return true;
else return false;
}
};代码2,是动规五部曲中递推公式中的那个,因为s是最长公共子序列子序列,所以只在t字符串中考虑是否删除元素从而达到减少字符而和字符串s匹配的目的
class Solution {
public:
bool isSubsequence(string s, string t) {
//定义并初始化dp数组
vector<vector<int>> dp(s.size()+1,vector<int>(t.size()+1,0));
int result = 0;
for(int i=1;i<=s.size();i++){
for(int j=1;j<=t.size();j++){
if(s[i-1]==t[j-1]) dp[i][j]=dp[i-1][j-1]+1;
else dp[i][j]=dp[i][j-1];
result = max(result,dp[i][j]);
}
}
if(result==s.size()) return true;
else return false;
}
};- 时间复杂度:O(n × m)
- 空间复杂度:O(n × m)
代码也可以这样
class Solution {
public:
bool isSubsequence(string s, string t) {
//定义并初始化dp数组
vector<vector<int>> dp(s.size()+1,vector<int>(t.size()+1,0));
for(int i=1;i<=s.size();i++){
for(int j=1;j<=t.size();j++){
if(s[i-1]==t[j-1]) dp[i][j]=dp[i-1][j-1]+1;
else dp[i][j]=dp[i][j-1];
}
}
if(dp[s.size()][t.size()]==s.size()) return true;
else return false;
}
};题目2:115 不同的子序列
题目链接:不同的子序列
对题目的理解
返回字符串t在字符串s的子序列中出现的个数 注意说的是s的子序列,不一定连续
题目保证答案符合 32 位带符号整数范围
动态规划
动规五部曲
1)dp数组及下标i的含义
dp[i][j] :以i-1为结尾的字符串s中有以j-1为结尾的字符串t的个数
2)递推公式
这一类问题,基本是要分析两种情况
- 当前两字符串末尾的字母相等,s[i - 1] 与 t[j - 1]相等
- 当前两字符串末尾的字母不等,s[i - 1] 与 t[j - 1] 不相等
s[i - 1] 与 t[j - 1]相等,dp[i][j]可以有两部分组成,(因为字符串s中,可能会包括相同字母顺序出现多次的情况)
1)使用当前的s[i - 1]匹配t[j-1],因为这两个字母已经相同了,所以不需要考虑当前s子串和t子串的最后一位字母s[i-1]和t[j-1]了,即只需要根据前面的s[i-2]和t[j-2]计算的dp[i-1][j-1]个数继续赋值就行,就看前面计算了多少个就可以了,这个继续向下进行赋值就OK
2)不使用当前的s[i - 1]来匹配t[j-1]
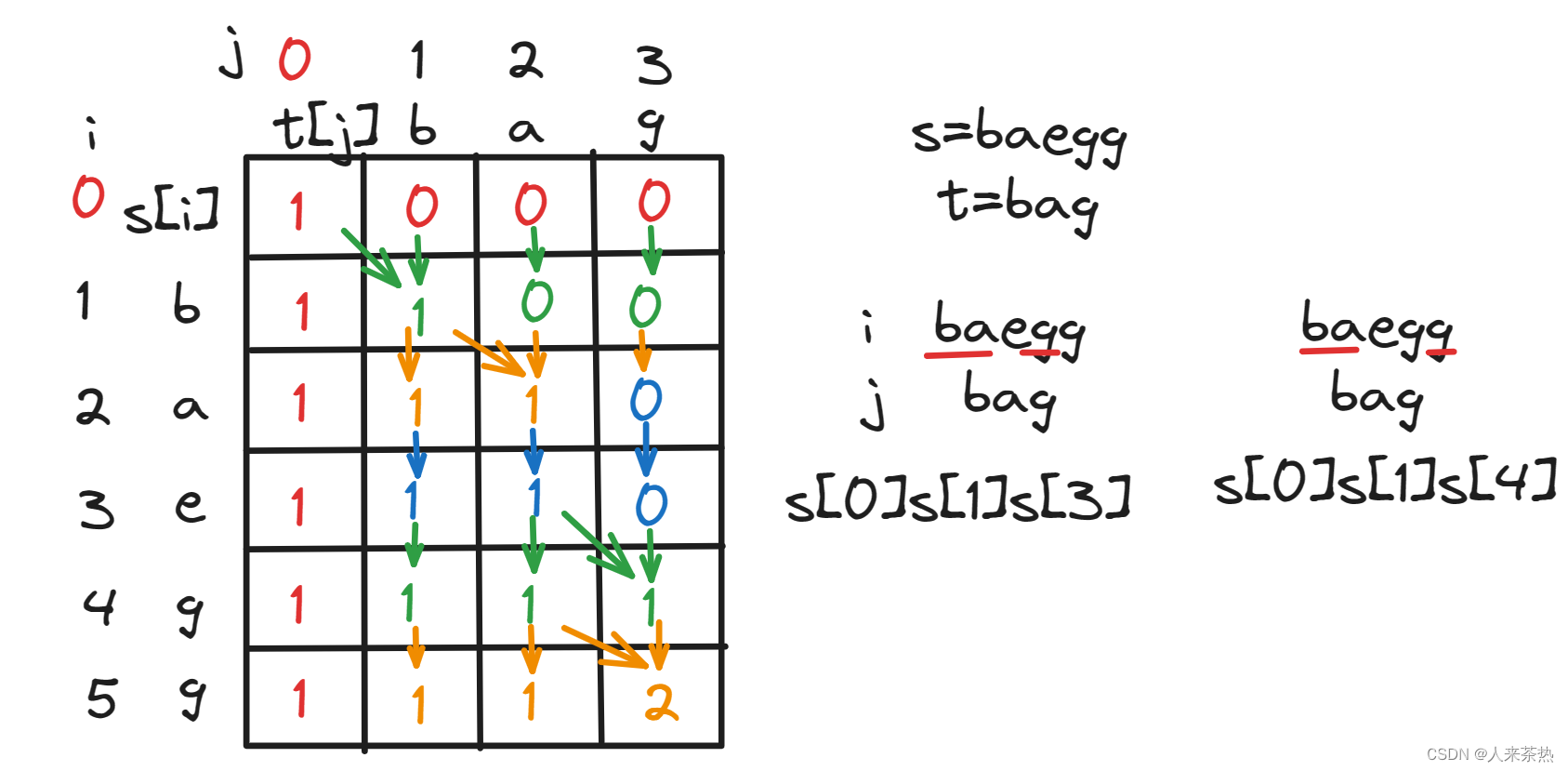
例如: s:bagg 和 t:bag ,s[2],s[3] 和 t[2]是相同的,可以用s[3]来匹配,也可以用s[2]匹配,
当s[3]和t[2]相匹配时,当前的s[i-1]与t[i-1]相匹配都对应着最后一个字母g,此时就是第一种情况,取决于dp[i-1][j-1];
但是不使用s[3](假设删除了元素s[3],也有可能和t相匹配),而是使用s[2]来匹配t[2]也是可以的,字符串t中要匹配的字母t[2]还是不变,只是s子串的最后一个字母发生了变化(由s[3]处的g变为s[2]处的g)而已,个数就为同样的t[j]在前面s[i-2]计算的个数,即对应着dp数组中的dp[i-1][j],
所以当s[i - 1] 与 t[j - 1]相等时,将这两种情况得到的结果进行相加,dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
当s[i - 1] 与 t[j - 1]不相等时,dp[i][j]只有一部分组成
因为两个子串最末尾的字符已经不等了,所以无法使用s[i-1]匹配t[j-1],则对于t[j-1]不考虑s[i-1],模拟将字符串中的s[i-1]这个元素删除,那么就拿上一层,也就是字符s[i-1]的前一个字符s[i-2]来匹配字符t[i-1]的结果来作为当前字符s[i-1]匹配t[j-1]的结果,
dp[i][j] = dp[i - 1][j]

3)dp数组初始化
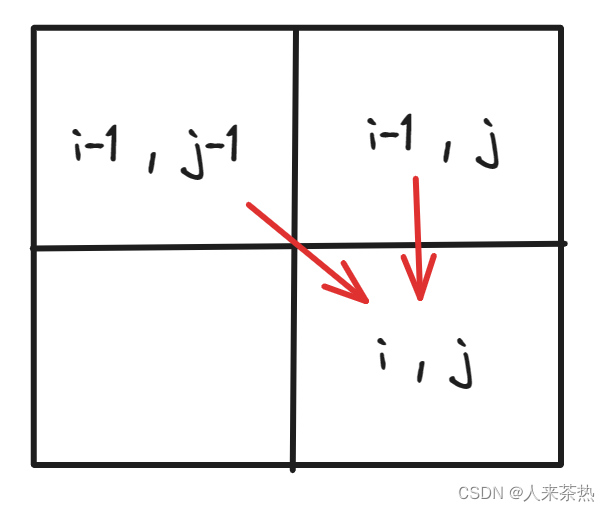
根据递推公式,dp[i][j]是从上方和左上方推导而来,第一行与第一列要进行初始化,是递推公式的基础。
根据dp数组定义,dp[i][0] 代表以i-1为结尾的字符串s中有以-1为结尾的空字符串t的个数,而s不为空,如果将s中的字符都删除,则会变成空字符串t ,则有一个
dp[0][j] 代表以-1为结尾的字符串s中有以j-1为结尾的t字符串的个数,此时s是空字符串,而t不是空字符串,所以无论怎么改变s,都没有办法组成t字符串,所以有0个
交集 dp[0][0] = 1 :空字符串s中有1个空i字符串t
4)遍历顺序
根据递推公式 从左到右,从上到下

5)打印dp数组
最终的结果是dp[s.size()][t.size()],因为最终一定要将字符串s和字符串t遍历完,才能最终判定字符串s中有多少个字符串t,这样才能不落掉任何一个字符,保证字符全部都遍历到,这样才能不落掉任何一个个数
代码
class Solution {
public:
int numDistinct(string s, string t) {
//定义并初始化dp数组
vector<vector<int>> dp(s.size()+1,vector<int>(t.size()+1,0));
//初始化dp数组
for(int i=0;i<s.size();i++) dp[i][0]=1;
for(int i=1;i<=s.size();i++){
for(int j=1;j<=t.size();j++){
if(s[i-1]==t[j-1]) dp[i][j]=dp[i-1][j-1]+dp[i-1][j];
else dp[i][j]=dp[i-1][j];
}
}
return dp[s.size()][t.size()];
}
};上述代码会报如下错误
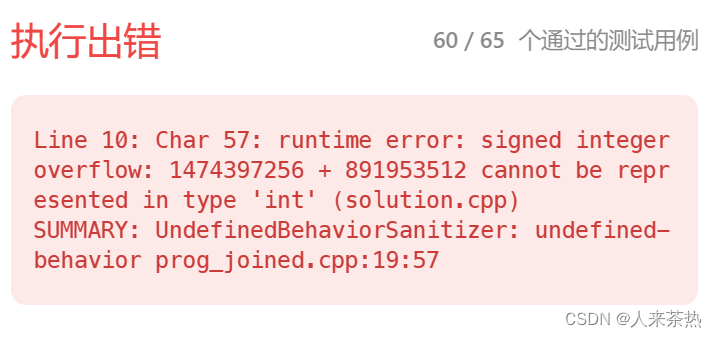 会有溢出错误,因为是两个整数相加,结果超出了int类型的表示范围
会有溢出错误,因为是两个整数相加,结果超出了int类型的表示范围
将代码改为如下
class Solution {
public:
int numDistinct(string s, string t) {
//定义并初始化dp数组
vector<vector<uint64_t>> dp(s.size()+1,vector<uint64_t>(t.size()+1,0));
//初始化dp数组
for(int i=0;i<s.size();i++) dp[i][0]=1;
for(int i=1;i<=s.size();i++){
for(int j=1;j<=t.size();j++){
if(s[i-1]==t[j-1]) dp[i][j]=dp[i-1][j-1]+dp[i-1][j];
else dp[i][j]=dp[i-1][j];
}
}
return dp[s.size()][t.size()];
}
};- 时间复杂度: O(n * m)
- 空间复杂度: O(n * m)
也可以将类型改为unsigned long long也能顺利通过,代码如下
class Solution {
public:
int numDistinct(string s, string t) {
//定义并初始化dp数组
vector<vector<unsigned long long>> dp(s.size()+1,vector<unsigned long long>(t.size()+1,0));
//初始化dp数组
for(int i=0;i<s.size();i++) dp[i][0]=1;
for(int i=1;i<=s.size();i++){
for(int j=1;j<=t.size();j++){
if(s[i-1]==t[j-1]) dp[i][j]=dp[i-1][j-1]+dp[i-1][j];
else dp[i][j]=dp[i-1][j];
}
}
return dp[s.size()][t.size()];
}
};流程