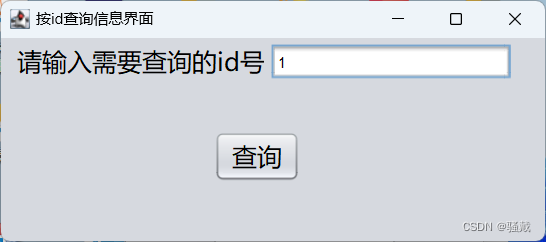
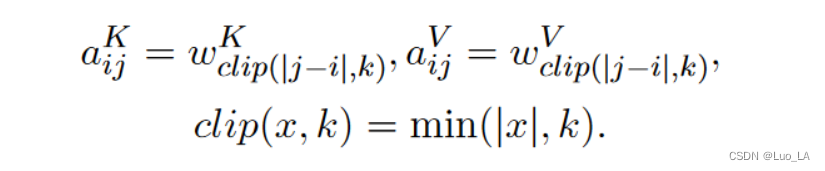A Transformer-based Approach for Source Code Summarization
- 1. Introduction
- 2. Approach
- 2.1 Architecture
- Self-Attention
- Copy Attention
- 2.2 Position Representations
- 编码绝对位置
- 编码成对关系
1. Introduction
生成描述程序功能的可读摘要称为源代码摘要。在此任务中,通过对代码标记之间的成对关系进行建模来捕获其远程依赖关系,对学习代码表示至关重要。为了学习摘要的代码表示,本方法探索了 Transformer 模型,该模型使用 self-attention 机制,并且已被证明可以有效捕获远程依赖关系。为了学习序列中标记的顺序并对标记之间的关系进行建模,Transformer 需要注入位置编码。在这项工作中,本方法表明,通过使用相对位置表示对源代码标记之间的成对关系进行建模,相较于使用绝对位置表示学习代码标记的序列信息会取得更显著的改进。
2. Approach
本方法提出在给定一段源代码的情况下使用 Transformer 生成自然语言摘要。代码和摘要都是由向量序列 x = (x1, …, xn) 表示的标记序列,其中 xi ∈ Rdmodel 。在本节中,将简要描述 Transformer 架构以及如何在 Transformer 中对源代码标记的顺序或其成对关系进行建模。
2.1 Architecture
Transformer 由编码器和解码器的堆叠多头注意力和参数化线性变换层组成。在每一层,多头注意力采用 h 个注意力头并执行自注意力机制。
Self-Attention
在每个注意力头中,输入向量序列 x = (x1, . . . , xn) (其中 xi ∈ Rdmodel)被转换为输出向量序列,o = (o1, . . . , on) 其中 oi ∈ Rdk:
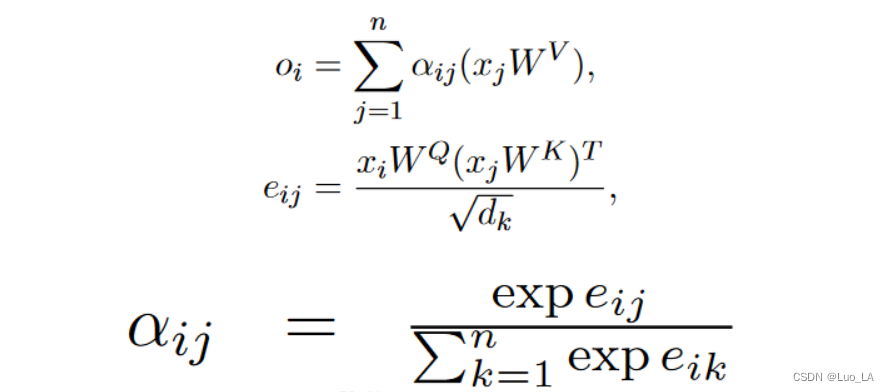
W
Q
,
W
K
W^Q,W^K
WQ,WK 在每一层的每一个头中都是唯一的参数。
Copy Attention
我们在 Transformer 中加入了复制机制,以允许从词汇表生成单词并从输入的源代码中进行复制。我们使用额外的注意力层来学习解码器堆栈顶部的副本分布。复制注意力使 Transformer 能够从源代码中复制罕见的标记(例如函数名称、变量名称),从而显着提高摘要性能。
2.2 Position Representations
现在,我们讨论如何学习源代码标记的顺序和建模它们的成对关系。
编码绝对位置
为了让 Transformer 利用源代码 token 的顺序信息,我们训练了一个嵌入矩阵 W P e W^{Pe} WPe ,它学习将 token 的绝对位置编码为 d m o d e l d_{model} dmodel 维度的向量。然而,我们表明,捕获代码标记的顺序对学习源代码表示没有帮助,并且会导致摘要性能较差。
编码成对关系
代码的语义表示不依赖于其标记的绝对位置。相反,它们的相互作用会影响源代码的含义。例如,表达式a+b和b+a的语义是相同的。
为了对输入元素之间的成对关系进行编码,将自注意力机制扩展如下。
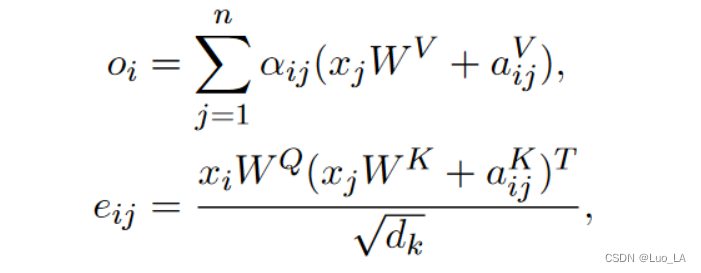
将输入元素之间的edge表示为
a
i
j
V
,
a
i
j
K
a_{ij}^V,a_{ij}^K
aijV,aijK
考虑到计算量、内存消耗以及远距离的精确位置信息效用足等因素,此方法对最远的相对位置距离限制为 k k k。
Relative Position Representation 的目标是给出
a
i
,
j
V
,
a
i
,
j
K
a_{i,j}^V,a_{i,j}^K
ai,jV,ai,jK 的计算方式。假设如果序列中两个元素的距离超过
k
k
k,则这两元素之间的位置信息就没有意义了。剪裁最大距离还使模型能够泛化训练期间看不到的序列长度,因此,考虑
2
k
+
1
2k+1
2k+1 个唯一的edge标签。
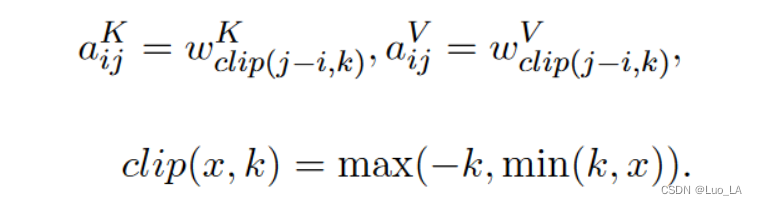
在这种设定下,
a
i
,
j
V
,
a
i
,
j
K
a_{i,j}^V,a_{i,j}^K
ai,jV,ai,jK 应该只与相对位置有关,而与
x
i
,
j
,
x
i
,
j
x_{i,j},x_{i,j}
xi,j,xi,j 没有关系。作者直接将
a
i
,
j
V
,
a
i
,
j
K
a_{i,j}^V,a_{i,j}^K
ai,jV,ai,jK 定义为可训练的向量,本质上是训练
w
K
=
(
w
−
k
K
,
.
.
.
,
w
k
K
)
w^K=(w_{-k}^K,...,w_k^K)
wK=(w−kK,...,wkK) 和
w
V
=
(
w
−
k
V
,
.
.
.
,
w
k
V
)
w^V=(w_{-k}^V,...,w_k^V)
wV=(w−kV,...,wkV),
w
i
K
,
w
i
V
∈
R
d
a
w_i^K,w_i^V∈\mathbb{R}^{d_a}
wiK,wiV∈Rda。
本方法研究了忽略方向信息的相对位置表示的替代方案。换句话说,第j个标记是在第i个标记的左边还是右边的信息被忽略。