回溯法概念

概念：在包含问题所有解的解空间树中，按照深度优先搜索的策略，根据根结点（开始节点）出发搜索解空间树。

流程：首先根结点成为活节点，同时也成为当前的扩展结点。在当前的扩展结点处，搜索向纵深方向移至一个新结点。这个新结点就成为新的活结点，并成为当前的扩展结点。如果在当前的扩展结点处不能再向纵向方向移动，则当前扩展结点就成为死结点。此时应往回移动（回溯）至最近的一个活结点处，并使这个活结点成为当前的扩展结点。回溯法以这种方式递归的在解空间中搜索，直到找到所要求的解或解空间中已无活结点为止

活结点（active node）：指自身已生成但其孩子结点没有全部生成的结点

扩展节点（expansion node）：指正在产生孩子结点的结点，也称E结点

死结点（dead node）：指其所有子结点均已生产的结点

保存结点的解：回溯法求解时存在退回到祖先结点的过程，所以需要保存搜索过的结点。通常有两种方法，其一是用自定义栈来保存祖先结点；其二是采用递归方法，因为递归调用会将祖先结点保存到系统栈中，在递归调用返回时自动回退到祖先结点。

避免无效搜索：回溯法搜索解空间时通常采用两种策略避免无效搜索，以提高回溯的搜索效率，一是用约束函数在扩展结点处剪除不满足约束条件的路径，二是用限界函数减去得不到问题解或最优解的路径，这两类函数统称为剪枝函数。

回溯法的解题步骤：

1. 针对给定的问题确定问题的解空间树，问题的解空间树应至少包含问题的一个解或最优解。
2. 确定结点的扩展搜索规则
3. 以深度优先方式搜索解空间树，并在搜索过程中采用剪枝函数来便面无效搜索。其中，深度优先方式可以选择递归回溯或者迭代（非递归）回溯

回溯算法与深度优先遍历的异同：

1. 访问次序不同
2. 访问次数不同
3. 剪枝不同

（1）访问次序不同：深度优先遍历的目的是“遍历”，本质是无序的，也就是说访问次序不重要，重要的是否被访问过（实现上只需要对于每个位置记录是否被访问就足够）。回溯法的目的是“求解过程”，本质是有序的，也就是说每一步都是要求的次序（实现上要使用访问状态来记录，也就是对于每个顶点记录以及访问过的邻居方向，回溯之后从新的未访问过的方向去访问其他邻居）。

（2）访问次序不同：深度优先遍历对已经访问过的顶点不再访问，所有顶点仅访问一次。回溯法中已经访问过的顶点可能再次访问

（3）剪枝不同：深度优先遍历不含剪枝，而很多回溯法会采用剪枝条件剪除不必要的分支以提高效能

回溯法的时间分析：

时间分析依据：解空间树中的结点数

假设：解空间树共有n层，第一层有m0个满足约束条件的结点，每个结点有m1个满足约束条件的结点，则第二层有m0m1（m2）个满足约束条件的结点，同理，第三层有m0m1m2个满足约束条件的结点......

执行时间：T(n)=m0+m0m1+m0m1m2+m0m1m2m3+....+m0m1m2...(mn-1)

时间复杂度：

1. 解空间树为子集树时：O(2^n)
2. 解空间树为排列树时：O(n!)

1、N皇后问题

八皇后问题是回溯算法的典型例题。该问题是十九世纪著名的数学家高斯1850年提出：在8X8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜率为1的斜线上，问有多少种摆法？（每一行应有一个皇后）

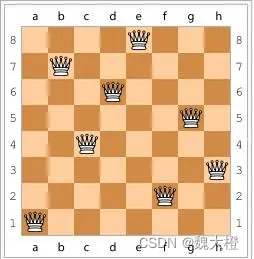
解决思路：

1. 解决皇后在棋盘上的攻击范围
2. 递归处理完成深度优先搜索并回溯过程
3. 进行调用的函数

put_queen函数：使用一个attack数组来存放皇后的攻击范围，1为不可放置区域，0为安全区域。dx与dy数组组合完成对八个方向的扩展，if判断语句来控制范围始终处于棋盘中

void put_queen(int x,int y,vector<vector<int>> &attack) {
	static const int dx[] = {-1,1,0,0,-1,-1,1,1 };
	static const int dy[] = { 0,0,-1,1,-1,1,-1,1 };
	attack[x][y] = 1;//皇后位置取值为1
	for (int i = 0; i < attack.size(); i++) {
		for (int j = 0; j < 8; j++){
			int nx = x + i * dx[j];
			int ny = y + i * dy[j];
			if (nx >= 0 && nx < attack.size() && ny >= 0 && ny < attack.size()) {
				attack[nx][ny] = 1;
			}
		}
	}
}

backtrack函数：当皇后放置完后，k溢出进行存储入solve数组操作，核心思想为下一层无无位置时进行回溯

void backtrack(int k,int n,vector<string> &queen,vector<vector<int>> &attack,vector<vector<string>> &solve){
		//k:表示当前处理的行数
		//n:表示N皇后问题
		//queen:存储皇后的位置
		//attack:标记皇后的攻击范围
		//solve:存储N皇后的解法
	if (k == n) {
		solve.push_back(queen);
		return;
	}
	//遍历
	for (int i = 0; i < n; i++) {
		if (attack[k][i] == 0) {
			vector<vector<int>> tmp = attack;//备份attack数组
			queen[k][i] = 'Q';
			put_queen(k, i, attack);//更新attack数组
			backtrack(k + 1, n, queen, attack, solve);//递归试探k+1行皇后位置
			attack = tmp;//恢复attack数组
			queen[k][i] = '.';//恢复queen数组
		}
	}
}

solveQueens函数：定义attack棋盘、solve解法保存数组、queen摆放方案，循环初始化数组

vector<vector<string>> solveQueens(int n) {
	vector<vector<string>> solve;
	vector<vector<int>> attack;
	vector<string> queen;
	//使用循环初始化attack和queen数组
	for (int i = 0; i < n; i++) {
		attack.push_back(std::vector<int>());
		for (int j = 0; j < n; j++) {
			attack[i].push_back(0);
		}
		queen.push_back("");
		queen[i].append(n, '.');
	}
	backtrack(0, n, queen, attack, solve);
	return solve;
}

主函数：

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);

	vector<vector<string>> result;
	result = solveQueens(8);//8皇后问题

	cout << "8皇后共有" << result.size() << "种解法" << endl;
	for (int i = 0; i < result.size(); i++) {
		cout << "解法" << i+1 << ":\n" << endl;
		for (int j = 0; j < result[i].size(); j++) {
			cout << result[i][j].c_str() << "\n" << endl;
		}
		cout << "\n" << endl;
	}
	return 0;
}