【华为OD题库-064】最小传输时延I-java

news2024/11/17 15:59:17

题目

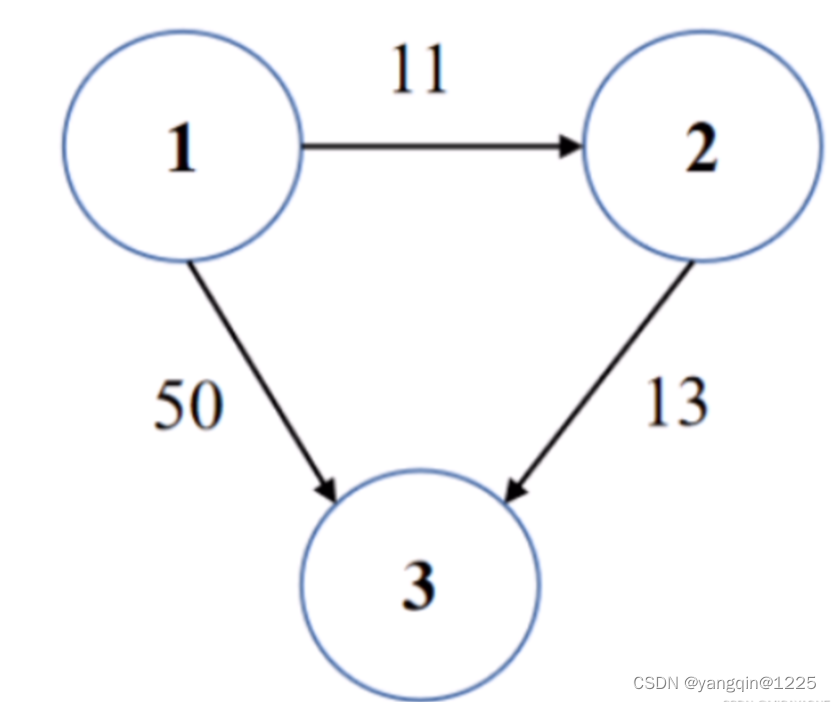
某通信网络中有N个网络结点，用1到N进行标识。网络通过一个有向无环图.表示,其中图的边的值表示结点之间的消息传递时延。
现给定相连节点之间的时延列表times[]={u，v， w)，其中u表示源结点，v表示目的结点，w表示u和v之间的消息传递的时延。请计算给定源结点到目的结点的最小传输时延，如果目的结点不可达，返回-1。
注:N的取值范围为[1，100];
时延列表times的长度不超过6000，且1<= u,v<= N，0<=w <= 100;
输入描述:
输入的第一行为两个正整数，分别表示网络结点的个数N，以及时延列表的长度M，用空格分隔;
接下来的M行为两个结点间的时延列表[u v w];
输入的最后一行为两个正整数，分别表示源结点和目的结点。

输出描述:
起点到终点得最小时延，不可达则返回-1
示例1:
输入:
3 3
1 2 11
2 3 13
1 3 50
1 3
输出:
24

思路

Dijkstra 算法，该算法B站视频讲解得较清楚
同leetcode： 743. 网络延迟时间

每次从未标记的节点中选择距离起点最近的节点，标记
计算刚加入节点A的邻近节点B的距离（不包含标记的节点），若（节点A的距离+节点A到节点B的边长）<节点B的距离，就更新节点B的距离

题解

package hwod;

import java.util.Arrays;
import java.util.Scanner;

public class TheLeastDelayTime {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt(), m = sc.nextInt();
        int[][] nums = new int[m][3];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < 3; j++) {
                nums[i][j] = sc.nextInt();
            }
        }
        int start = sc.nextInt(), end = sc.nextInt();
        System.out.println(theLeastDelayTime(nums, n, start, end));
    }

    private static int theLeastDelayTime(int[][] nums, int n, int start, int end) {
        int[][] g = new int[n][n];
        final int INF = Integer.MAX_VALUE / 2;//防止越界
        for (int i = 0; i < n; i++) {
            Arrays.fill(g[i], INF);
        }
        for (int[] t : nums) {
            int x = t[0] - 1, y = t[1] - 1;
            g[x][y] = t[2];
        }
        int[] used = new int[n];
        int[] dist = new int[n];
        Arrays.fill(dist, INF);
        dist[start - 1] = 0;
        for (int i = 0; i < n; i++) {
            int x = -1;//未标记的距离start最近的节点
            //更新未标记的，距离start最近的节点
            for (int y = 0; y < n; y++) {
                if (used[y] == 0 && (x == -1 || dist[y] < dist[x])) {
                    x = y;
                }
            }
            used[x] = 1;
            for (int y = 0; y < n; y++) {
                dist[y] = Math.min(dist[y], dist[x] + g[x][y]);
            }
        }
        return dist[end - 1] == INF ? -1 : dist[end - 1];

    }
}