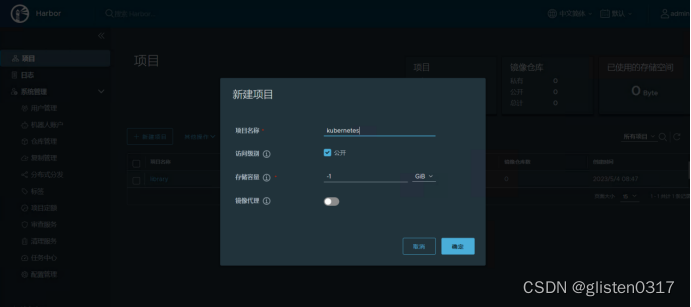
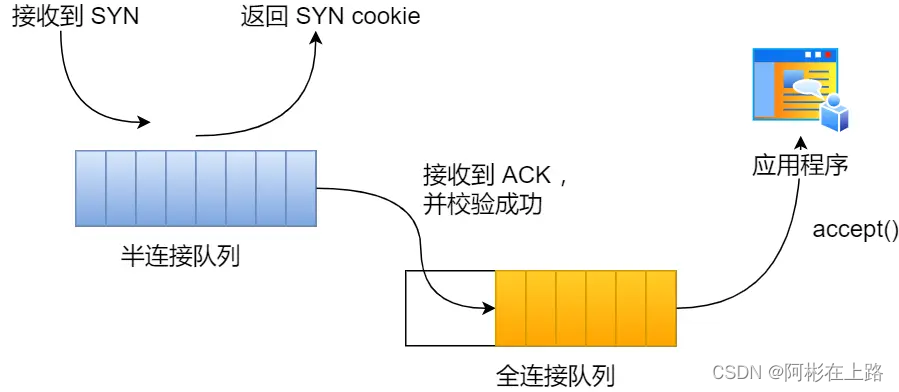
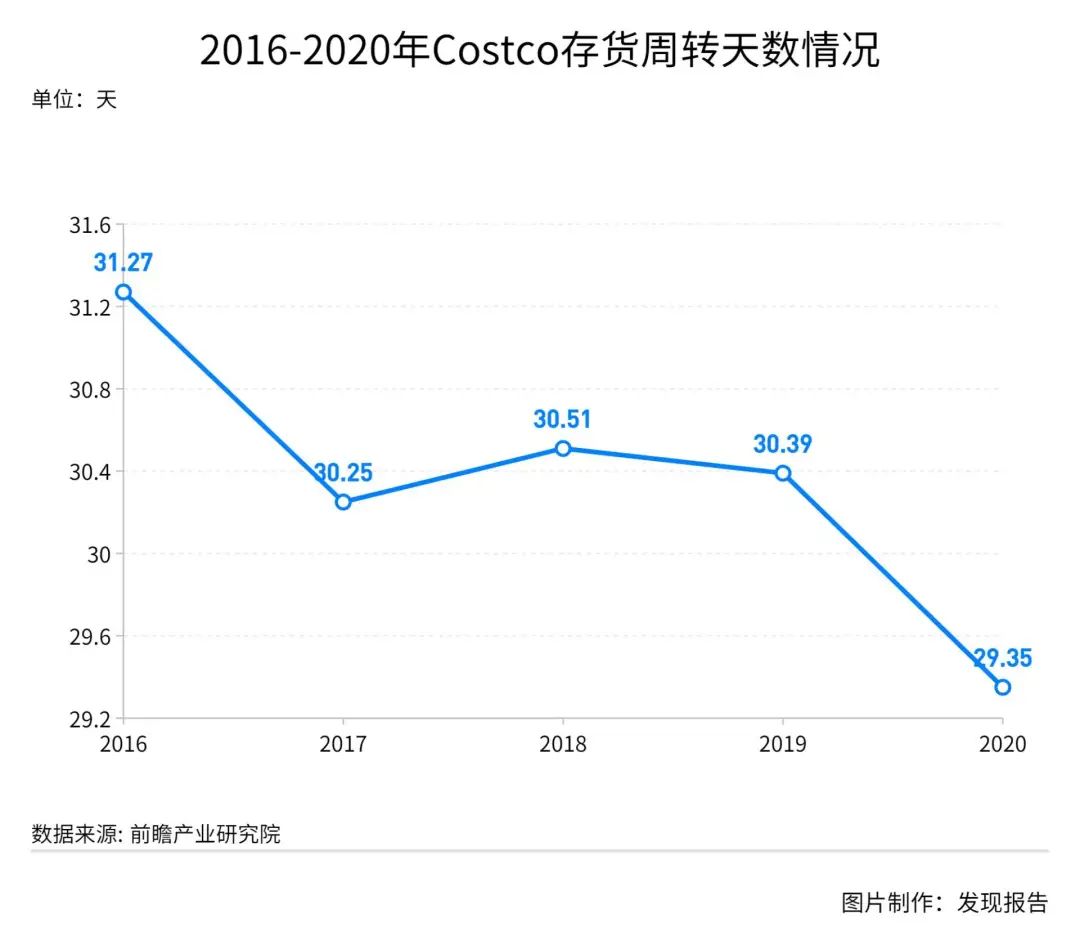
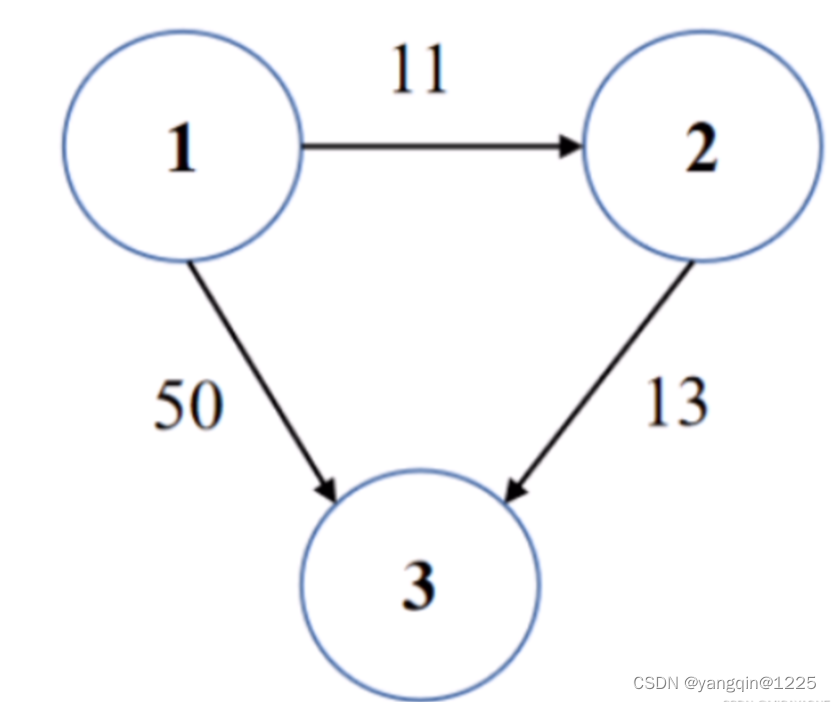
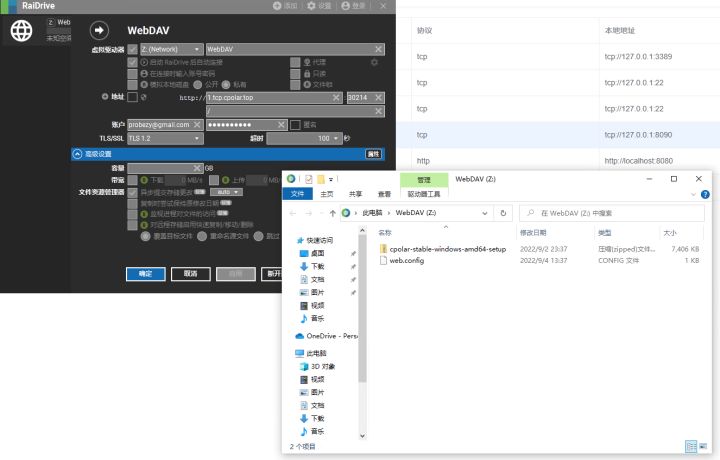
import java.io.*;

/*先找后两个数for(int i = 0; 2 * i * i <= n;i++)
                for(int j = i; i * i + j * j <= n;j ++)
再找前两个数  for(int i = 0;4 * i * i <= n; i ++)
                 for(int j = i;2 * (j * j + i * i) <= n;j ++)
            //这样就可以让后两个数尽量大,前两个数尽量小     这样就可以确定后两个数一定大于前两个数
            //第一次遍历到的值就是字典序列最小的值  
            //比如找后两个数(1,9)一定比 (5,5) 更早遍历到 这样就保证是字典序列 
(用st数组记录某个数是否用过，只需要记录第一次被枚举到的数),

*/
public class Main
{
    static int n;
    static int N = 5000000;
    static boolean[] st = new boolean[N];
    static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
    static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
    static PII[] p = new PII[N];
    //后来存储后两个数对应的下标数对
    
    public static void main(String[] args) throws IOException
    {
        n = Integer.parseInt(in.readLine());
        
        //这里两层循环可以等,是为了让他们更接近n
        for(int i = 0; 2 * i * i <= n;i++)
        {
                for(int j = i; i * i + j * j <= n;j ++)
                {
                    int x = i * i + j * j;
                    if(!st[x]){
                        st[x] = true;
                        p[x] = new PII(i,j);
                    }
                }
        }
        
        
        //从小到大枚举,第一次遇到的就是字典序列最小的
        //这里两次循环最好不要等,这样就可以尽量小
        for(int i = 0;4 * i * i < n; i ++)
        {
            for(int j = i;2 * (j * j + i * i) < n;j ++)
            {
                int t = n - j * j - i * i;
                if(st[t])
                {
                    System.out.println(i + " " + j + " " + p[t].x + " " + p[t].y);
                    return;
                }
            }
        }
        in.close();
        out.flush();
    }
    static class PII
    {
        int x,y;
        public PII(int x,int y)
        {
            this.x = x;
            this.y = y;
        }
    }
}