一、为什么要进行时序分析和时序约束
PCB通过导线将具有相关电气特性的信号相连接,这些电气信号在PCB上进行走线传输时会产生一定的传播延时。
而FPGA内部也有着非常丰富的可配置的布线资源,能够让位于不同位置的逻辑资源块、时钟处理单元、BLOCK RAM、DSP和接口模块等资源能够相互通信,完成所需功能。
FPGA的布线同PCB的走线一样,也会由于走线的长短不同而产生或大或小的传输延时(走线延时)。FPGA信号经过逻辑门电路进行各种运算也会产生延时(逻辑延时)。那么多个信号从FPGA的一端输入,经过一定的逻辑门电路处理后从FPGA的另一端输出,如何保证各个信号的延时一致呢?这个时候就需要进行时序分析,从而进行时序约束,从而保证FPGA的信号能够相互协同正常工作。
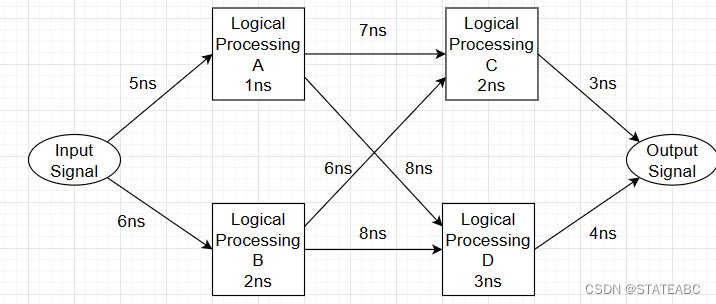
假设有一个信号输入FPGA中,在FPGA内部经过一些逻辑处理,最后进行输出,那么这些走线和处理都需要时间(走线延时和逻辑延时)。例如下图,输入信号到达逻辑处理A需要5ns,进行处理需要1ns,然后到逻辑处理C需要7ns,进行处理需要2ns,最后达到输出需要3ns,这条路径是所有路径中耗时最短的。但是FPGA不知道这条路径耗时最短,如果不对其进行时序约束,很可能会随便选一条路径进行布线,此时如果对系统的延时有要求,就可能出现信号错乱的情况。
二、什么是时序分析和时序约束
FPGA的时序分析与约束需要设计者根据实际的系统功能,通过时序约束的方式提出时序要求;FPGA编译工具根据设计者的时序要求,进行布局布线;编译完成后,FPGA编译工具还需要针对布局布线的结果,套用特定的时序模型,给出最终的时序分析和报告;设计者通过查看时序报告,确认布局布线后的时序结果是否满足设计要求。
因此时序分析就是遍历电路存在的所有时序路径,计算信号在这些路径上的传播延时,使用特定的时序模型,针对特定的电路进行分析系统时序是否满足要求。
时序约束就是对设计的电路提出时序上的要求,一般来说其可以细分为内部时钟约束 、IO口时序约束、偏移约束、静态路径约束和例外路径约束等。
三、时序约束的基本路径
从前面知道了时序分析是遍历电路存在的所有时序路径,那么就需要知道都有哪些路径
FPGA 时序约束所覆盖的时序路径主要有4种:
1.FPGA内部寄存器之间的时序路径,即reg2reg;
2.输人引脚到FPGA内部寄存器的时序路径,即pin2reg;
3.FPGA内部寄存器到输出引脚的时序路径,即reg2pin;
4.输入引脚到输出引脚之间的时序路径(不通过寄存器),即pin2pin。
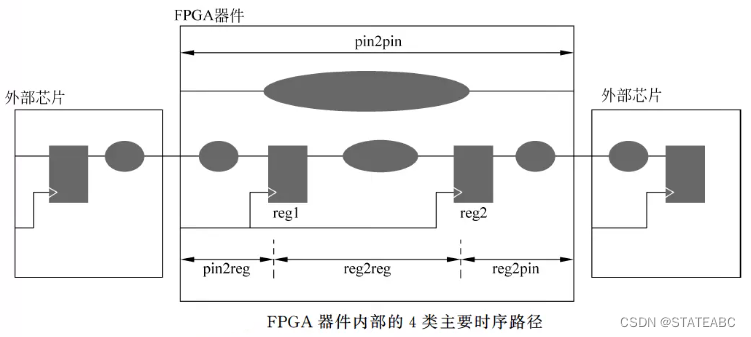
其中reg2reg、pin2reg、reg2pin都和寄存器有关,需要进行时序约束,因为要确保数据信号在时钟锁存沿的建立时间和保持时间内稳定;但pin2pin本质就是纯组合逻辑电路,一般直接约束延时范围,因为pin2pin路径的信号传输通常不通过时钟。
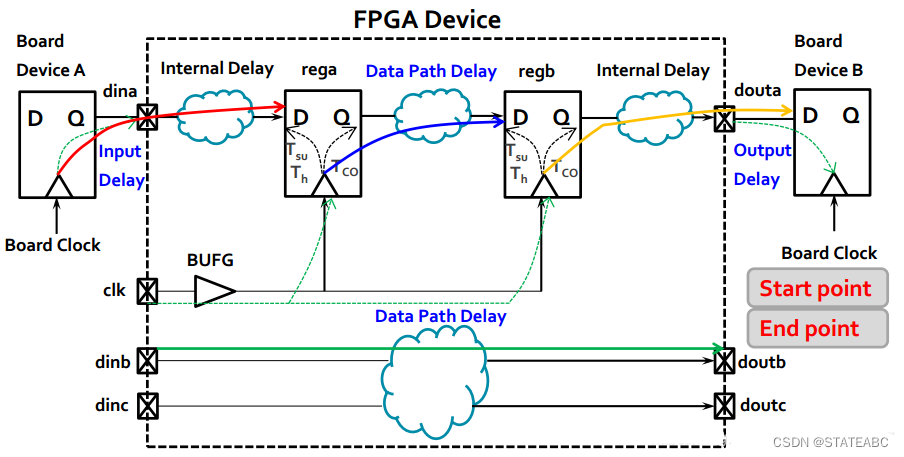
在4种时序路径中,
pin2reg需要经过3个延迟,例如Device A到rega需要经过Tco(寄存器输出延时)、Input Delay(输入走线延迟)、Internal Delay(FPGA内部走线延迟);
reg2reg需要经过2个延迟,例如rega到regb需要经过Tco、Data Path Delay(FPGA内部组合逻辑和数据走线延迟);
reg2pin需要经过3个延迟,例如regb到Device B需要经过Tco、Internal Delay、Output Delay(输出走线延迟);
pin2pin需要经过1个延迟,例如dinb到doutb需要经过Data Path Delay。
四、时序分析与约束的基本概念
知道有哪些路径之后, 就要明白时序分析、约束具体在分析约束什么数据或者参数,因此就需要从一些基本概念入手,理清楚要根据什么去进行分析和约束
4.1 Clock Uncertainty
时钟不确定性(Clock Uncertainty)主要由时钟抖动(Clock Jitter)和时钟偏差(Clock Skew)构成。
一个理想的时钟是占空比为50%且周期固定的方波,但实际上这样的时钟是不存在的,一定会有超前或者滞后的偏移,即时钟抖动。
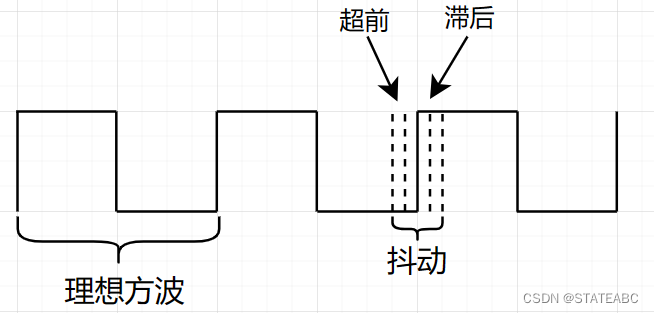
时钟偏差是指同一个时钟域内的时钟信号到达数字电路各个部分(一般指寄存器)所用时间的差异。

所以要对Clock Uncertainty进行约束,使时钟更加贴合实际。
4.2 建立时间和保持时间
建立时间( Setup Time,Tsu),在时钟上升沿之前数据必须稳定的最短时间。若不满足 setup time,数据无法进入寄存器,数据采样失败。
保持时间(Hold Time,Th),即在时钟上升沿之后数据必须稳定的最短时间。若不满足 hold time,数据也无法进入寄存器,数据采样失败。

寄存器采样需要同时满足建立时间和保持时间才能保证采样成功,因此也要对建立时间和保持时间进行约束。
4.3 发起沿和采样沿
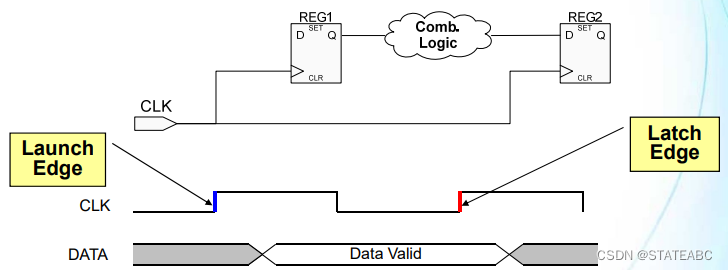
寄存器发送数据和接收数据需要在时钟边沿进行,因此都有一个发起沿和一个采样沿。通常情况下这两个边沿会有一个时钟周期的差别。
发起沿(Launch edge)是发送数据的时钟边沿,通常选择上升沿。发起沿是源寄存器采样的时间点,也是时序分析路径的起点。
采样沿(Capture edge)是采样到该数据的时钟边沿,通常也是上升沿。采样沿是目的寄存器采样的时间点,也是时序分析路径的终点。
4.4 数据到达时间和时钟达到时间
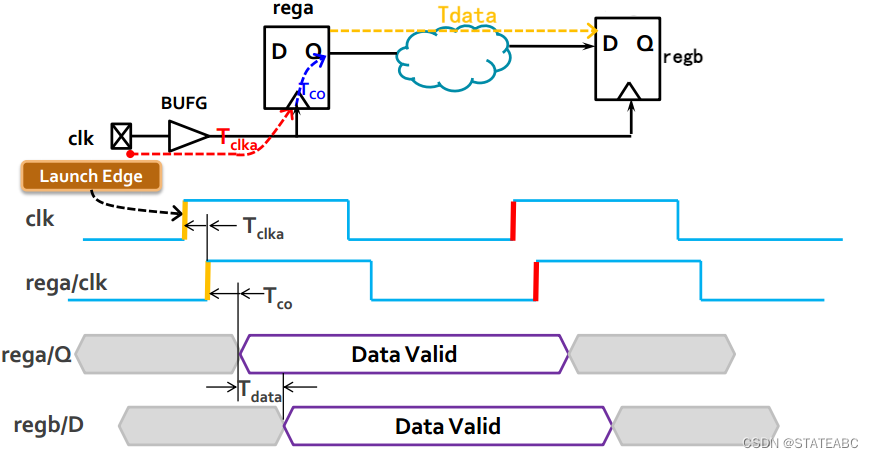
源寄存器rega在clk的上升沿发送数据,要经过一个时间才能到达目的寄存器regb(原因就是有走线、寄存器输出、逻辑处理延时),而这个时间则被称为数据到达时间(Data Arrival Time)。
通常选择发送沿Launch edge作为零时刻基准,数据经过Tclka(时钟信号从起点到寄存器时钟端口的时钟延时)、Tco时间,到达Q端口点,再从rega的Q端口经过组合逻辑以及布线的线延时(Tdata)到达接收端的D端口。
因此有公式:

目的寄存器对数据进行采样,4.3中提到通常情况下发送沿和采样沿会有一个时钟周期的差别,因此采样沿时间Capture Edge就是发送沿Launch edge+一个时钟周期clkb。
所以时钟到达时间(Clock Arrival Time)为
4.5 建立时间下的数据需求时间
前面我们知道在时钟上升沿之前数据必须稳定的最短时间为建立时间,那么对于reg2来说,要想满足建立时间,就必须要在建立时间之前接收到reg1的数据,这个时间就是建立时间下的数据需求时间(Data Required Time - Setup)
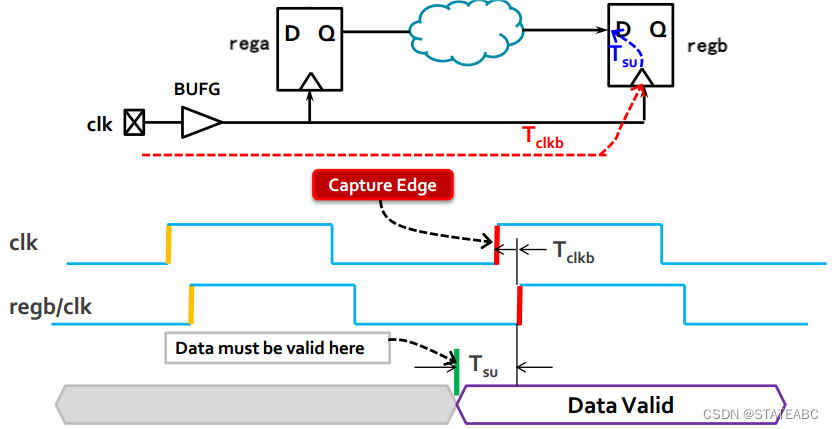
因此
4.6 保持时间下的数据需求时间
同理,时钟上升沿之后数据必须稳定的最短时间为保持时间,那么当regb采样到数据之后要满足保持时间,那么这个时间就是保持时间下的数据需求时间(Data Required Time - Hold)
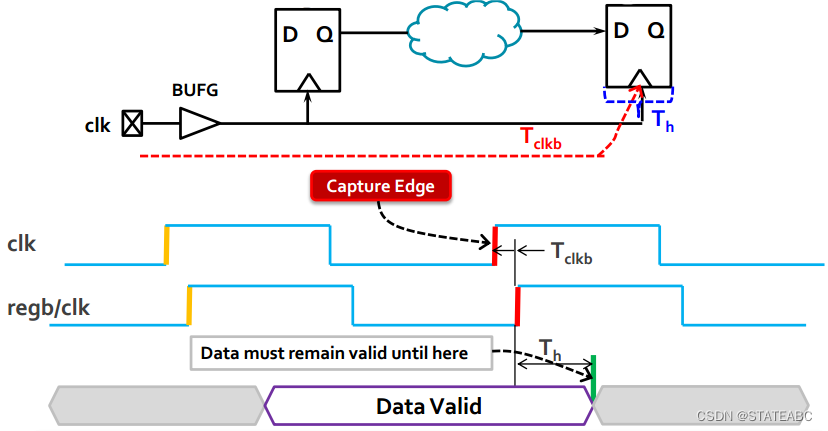
因此
4.7 建议时间裕量
在4.5中得到了寄存器满足建立时间下数据接收时间,例如时钟到达时间为5ns,建立时间Tsu为2ns,暂且将时钟不确定忽略,那么上一级数据到达最晚为5-2=3ns,因此上一级数据可以在1ns、2ns的时候到达。
如果数据在1ns到达目标寄存器,那么建立时间裕量(Setup slack)就是3-1=2ns。

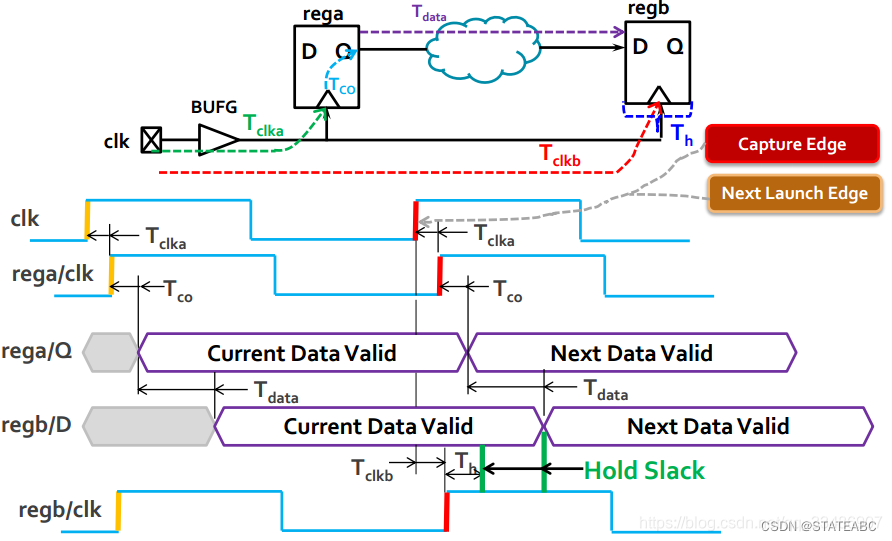
4.8 保持时间裕量
保持时间裕量(Hold slack)同理。
参考文献:
《FPGA时序约束与分析》
《正点原子FPGA静态时序分析与时序约束》
《Intel Quartus Prime Standard Edition用户指南: Timing Analyzer》
《Vivado Design Suite 用户指南: 设计分析与收敛技巧 (UG906)》