使用VC++设计程序实现K近邻中值滤波器（KNNMF）、最小均方差滤波器、矢量中值滤波算法进行滤波

news2025/1/17 3:36:12

VC++实现若干种图像滤波技术2

获取源工程可访问gitee可在此工程的基础上进行学习。
该工程的其他文章：
01- 一元熵值、二维熵值
02- 图像平移变换，图像缩放、图像裁剪、图像对角线镜像以及图像的旋转
03-邻域平均平滑算法、中值滤波算法、K近邻均值滤波器
04-分段线性变换，直方图均衡化、锐化处理
05-基于拉普拉斯算子、Canny的边缘检测功能、实现Otsu分割方法
06-最近邻插值，双线性插值，立方卷积插值
07-全局固定阈值分割、自适应阈值分割

文章目录

  • VC++实现若干种图像滤波技术2
    • 实验要求
    • 一、K近邻中值滤波器（KNNMF）
      • 1. K近邻中值滤波器（KNNMF）原理
      • 2. K近邻中值滤波器（KNNMF）实验代码
      • 3. K近邻中值滤波器（KNNMF）实验现象
    • 二、 最小均方差滤波器
      • 1. 最小均方差滤波器原理
      • 2. 最小均方差滤波器实验代码
      • 3. 最小均方差滤波器实验现象
    • 彩色图像矢量中值滤波算法
      • 1. 矢量中值滤波算法原理
      • 2. 矢量中值滤波算法实验代码
      • 3. 矢量中值滤波算法实验现象

实验要求

B部分：
（1）包括A部分全部要求。
（2）使用VC++设计程序：对一幅256级灰度图像，分别使用K近邻中值滤波器（KNNMF）、最小均方差滤波器进行滤波。
（3）使用VC++设计程序：对一幅24位彩色图像，使用矢量中值滤波算法进行滤波。

一、K近邻中值滤波器（KNNMF）

1. K近邻中值滤波器（KNNMF）原理

KNNMF（K-Nearest Neighbors Mean Filter）是一种非线性滤波算法，它利用每个像素点周围的 K 个最近邻居的平均值进行图像平滑。与传统的平均滤波器不同，KNNMF选择最相似的像素进行平均，这有助于在滤波的同时更好地保留图像的细节。

以下是KNNMF的基本步骤：

  1. 选择邻居数量K和滤波器大小： 确定每个像素点周围邻居的数量 K，同时选择一个滤波器的大小，通常是一个 n × n n \times n n×n 的窗口，其中 n n n为奇数。

  2. 遍历图像像素： 对于图像中的每个像素，以其为中心取一个 n × n n \times n n×n 的窗口。

  3. 计算邻居的相似度： 计算窗口内每个像素与中心像素的相似度，可以使用像素值之间的距离来衡量相似度。

  4. 选择相似度最高的 K 个邻居： 选择相似度最高的 K 个邻居进行平均。

  5. 更新像素值： 将该像素的值替换为相似度最高的 K 个邻居的平均值。

KNNMF算法相对于传统的平均滤波器，更注重选择相似度高的邻居进行平均，这有助于更好地保留图像的特征。在实际应用中，相似度的计算可以采用不同的度量方式，例如欧氏距离、余弦相似度等，具体取决于图像的特点和应用场景。

2. K近邻中值滤波器（KNNMF）实验代码

void CImageProcessingView::OnEnhanceDenoiseKNNMF()
{
 // 实验 图像平滑 256级灰度图像 KNNMF滤波
 // 参考 CImageProcessingView::OnEnhanceDenoiseAverage()
 //MessageBox("请在这里设计 256级灰度图像 KNNMF滤波 算法");
 
 // 获得当前文档对象
    CImageProcessingDoc* pDoc = GetDocument();
 if( pDoc->m_pDibInit->IsEmpty() )
 {
  MessageBox("图像未加载");
  return;
 }
  // 获得图像的基本信息
 int width = pDoc->m_pDibInit->GetWidth();
 int height = pDoc->m_pDibInit->GetHeight();
 int bitCount = pDoc->m_pDibInit->GetBitCount();

 // 程序只支持处理灰度图像
 if( bitCount!=8 )
 {
  MessageBox("目前只支持256级灰度图像");
  return;
 }

    // 将图像信息复制至 m_pDibTest
    pDoc->m_pDibTest->CloneDib(pDoc->m_pDibInit);
  
 //**********KNNMF滤波 算法**************//
 int i,j,m,n;
 BYTE grays[100];
 int graysSize = 100;
 int templateWidth = 3;
 int templateHeight = 3;
 int templateElementCnt = templateWidth*templateHeight;
 BYTE tempByte1;
 int kNN = 3;

 for(i=templateWidth/2; i<pDoc->m_pDibInit->m_lpBMIH->biWidth-templateWidth/2; i++)
 {
  for(j=templateHeight/2; j<pDoc->m_pDibInit->m_lpBMIH->biWidth-templateHeight/2; j++)
  {    
   memset(grays, 0, graysSize*sizeof(BYTE));

   for(n=0; n<templateHeight; n++)
   {
    for(m=0; m<templateWidth; m++)
    {    
     grays[n*templateWidth+m] = pDoc->m_pDibInit->GetPixelGray(i-templateWidth/2+m, j-templateHeight/2+n);
    }
   }
   
   BYTE centerGray = pDoc->m_pDibInit->GetPixelGray(i, j);

   for(m=0; m<templateElementCnt-1; m++)
   {
    for(n=m+1; n<templateElementCnt; n++)
    {
     if( abs(grays[m]-centerGray) > abs(grays[n]-centerGray) )
     {
      tempByte1 = grays[m];
      grays[m] = grays[n];
      grays[n] = tempByte1;
     }
    }
   }

  int midgray = 0;//中值
  for (m = 1; m <= kNN/2 ; m++)
   midgray = grays[m];
  pDoc->m_pDibTest->SetPixelGray(i, j, midgray);
  }
 }

  // 交换指针
 CDib* pTmpDib = pDoc->m_pDibTest;
 pDoc->m_pDibTest = pDoc->m_pDibInit;
 pDoc->m_pDibInit = pTmpDib; 
 // 设置脏标记
 pDoc->SetModifiedFlag(TRUE);
 
 // 更新视图
 pDoc->UpdateAllViews(NULL);
}

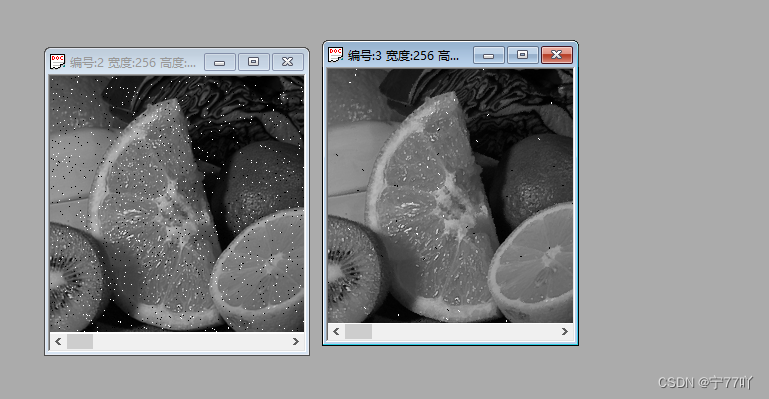
3. K近邻中值滤波器（KNNMF）实验现象

在这里插入图片描述

二、 最小均方差滤波器

1. 最小均方差滤波器原理

最小均方差滤波是一种图像处理中常用的滤波方法，其目标是通过在像素邻域内选择合适的权重，使得滤波后的像素值与邻域内的像素值之间的均方差最小。

滤波过程中，对于每个像素，通过选取邻域内的像素进行加权平均，其中每个像素的权重由该像素与中心像素之间的差异以及一个权重函数决定。权重函数通常是关于像素差异的一个单调递减函数，以便更重视与中心像素相似的像素。

最小均方差滤波的目标函数可以表示为：

E ( u , v ) = ∑ i = − N N ∑ j = − N N w [ i , j ] ( I ( u + i , v + j ) − T ( u , v ) ) 2 E(u,v) = \sum_{i=-N}^{N} \sum_{j=-N}^{N} w[i,j](I(u+i,v+j) - T(u,v))^2 E(u,v)=i=−N∑N​j=−N∑N​w[i,j](I(u+i,v+j)−T(u,v))2

其中：

  • $ (u,v) $ 是滤波后图像中的像素位置。
  • $ (i,j) $ 是邻域内像素的偏移。
  • $ I(u+i,v+j) $ 是邻域内某个像素的灰度值。
  • $ T(u,v) $ 是中心像素的灰度值。
  • $ w(i,j) $ 是权重函数。

最小均方差滤波的目标是找到使得目标函数 ( E(u,v) ) 最小的滤波器系数。这通常通过最小化目标函数的导数为零来实现。

具体实现最小均方差滤波需要对权重函数、邻域大小等进行合理的选择，以适应不同的图像处理任务。

2. 最小均方差滤波器实验代码

//**********最小均方差滤波算法**************//
int templateWidth = 3;
int templateHeight = 3;

for (int i = templateWidth / 2; i < width - templateWidth / 2; i++)
{
 for (int j = templateHeight / 2; j < height - templateHeight / 2; j++)
 {
  double minMSE = DBL_MAX; // 最小均方差初始化为最大值
  int optimalGray = 0;

 // 尝试所有可能的灰度值
  for (int k = 0; k <= 255; k++)
  {
   double mse = 0.0;

   // 计算邻域内所有像素与当前灰度值的均方差
   for (int n = 0; n < templateHeight; n++)
   {
    for (int m = 0; m < templateWidth; m++)
    {
     BYTE pixelValue = pDoc->m_pDibInit->GetPixelGray(i - templateWidth / 2 + m, j - templateHeight / 2 + n);
     mse += pow(pixelValue - k, 2);
    }
   }

   mse /= (templateWidth * templateHeight); // 均方差

   // 更新最小均方差和对应的灰度值
   if (mse < minMSE)
   {
    minMSE = mse;
    optimalGray = k;
   }
  }

  // 将最小均方差对应的灰度值设置为新的像素值
  pDoc->m_pDibTest->SetPixelGray(i, j, optimalGray);
 }
}

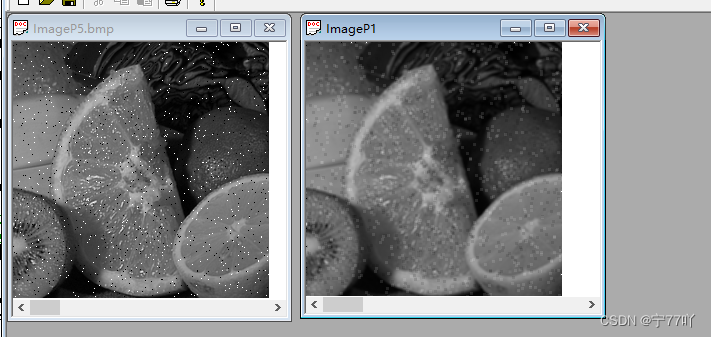
3. 最小均方差滤波器实验现象

左：加入噪声的图像
右：进行滤波后的图像

在这里插入图片描述

彩色图像矢量中值滤波算法

1. 矢量中值滤波算法原理

矢量中值滤波算法是一种基于中值运算的图像平滑处理方法。其原理可以概括为以下几个步骤：

  1. 选择邻域： 对于图像中的每个像素，定义一个邻域，包含该像素及其周围的像素。邻域的大小由窗口大小确定。

  2. 构建邻域矩阵： 将邻域内的像素值按某种顺序排列，形成一个矢量。这个矢量包含了邻域内所有像素的灰度值。

  3. 中值运算： 对构建的矢量进行中值运算，即找到矢量中的中间值。这可以通过对矢量进行排序，然后选择排序后的中间值来实现。

  4. 更新像素值： 将中值作为原始像素的新值，用于替代原始像素的灰度值。这样，经过矢量中值滤波处理后，图像中的每个像素都会得到一个中值平滑的结果。

矢量中值滤波的优点在于对图像进行平滑处理的同时能有效抑制噪声，特别适用于去除图像中的椒盐噪声等离群点。这种滤波方法在一些图像处理任务中取得了较好的效果，但也需要根据具体应用场景选择合适的窗口大小和滤波算法。

举个例子说明一下
假设我们有一个3x3的邻域矩阵，其像素值如下：

[ 10 20 15 30 25 40 35 15 20 ] \begin{bmatrix} 10 & 20 & 15 \\ 30 & 25 & 40 \\ 35 & 15 & 20 \\ \end{bmatrix} ​103035​202515​154020​ ​

现在我们要进行矢量中值滤波，按照步骤来进行处理：

  1. 选择邻域： 我们选择一个3x3的邻域，以中心像素25为例。

  2. 构建邻域矩阵： 将邻域内的像素值按顺序排列成矢量：

$ \text{矢量} = [10, 20, 15, 30, 25, 40, 35, 15, 20] $

  1. 中值运算： 对矢量进行排序，得到：
    $\text{矢量} = [10, 15, 15, 20, 20, 25, 30, 35, 40] $

中值是排序后的中间值，即 $\text{中值} = 20 $。

  1. 更新像素值： 将中值20作为原始像素25的新值。

这样，经过矢量中值滤波处理后，中心像素的值由原来的25变为20。这个过程对图像中的每个像素都进行，以达到平滑图像的目的。这种方法在处理一些椒盐噪声等离群点时具有较好的效果。

2. 矢量中值滤波算法实验代码

//**********矢量中值滤波算法**************//
 int templateWidth = 3;
 int templateHeight = 3;
 int templateElementCnt = templateWidth * templateHeight;
 
 int color_r[100][100] = { 0 };
 int color_g[100][100] = { 0 };
 int color_b[100][100] = { 0 };


 for (int i = templateWidth / 2; i < pDoc->m_pDibInit->m_lpBMIH->biWidth - templateWidth / 2; i++)
 {
  for (int j = templateHeight / 2; j < pDoc->m_pDibInit->m_lpBMIH->biWidth - templateHeight / 2; j++)
  {
   // 获取当前像素点邻域的颜色信息
   for ( n = 0; n < templateHeight; n++)
    for ( m = 0; m < templateWidth; m++)
    {
     RGBQUAD quad;
     quad = pDoc->m_pDibInit->GetPixelColor(i - templateWidth / 2 + m, j - templateHeight / 2 + n);
     color_r[n][m] = quad.rgbRed;
     color_g[n][m] = quad.rgbGreen;
     color_b[n][m] = quad.rgbBlue;
    }

   int sum_r = 0, sum_g = 0, sum_b = 0;
   for ( n = 0; n < templateHeight; n++)
    for ( m = 0; m < templateWidth; m++)
    {
     sum_r += color_r[n][m];
     sum_g += color_g[n][m];
     sum_b += color_b[n][m];
    }
   
   int avl_r = sum_r / templateElementCnt;
   int avl_g = sum_g / templateElementCnt;
   int avl_b = sum_b / templateElementCnt;

   float min = 255;  //最小的r
   RGBQUAD Quad;
   for ( n = 0; n < templateHeight; n++)
    for ( m = 0; m < templateWidth; m++)
    {
     // 计算中值
     float temp = (pow((color_r[n][m] - avl_r), 2) + pow((color_g[n][m] - avl_g), 2) + pow((color_b[n][m] - avl_b), 2)) / 2;
     if (temp < min)
     {
      Quad.rgbRed = color_r[n][m];
      Quad.rgbGreen = color_g[n][m];
      Quad.rgbBlue = color_b[n][m];
      min = temp;
     }
    }
   pDoc->m_pDibTest->SetPixelColor(i, j, &Quad);
  }
 }

3. 矢量中值滤波算法实验现象

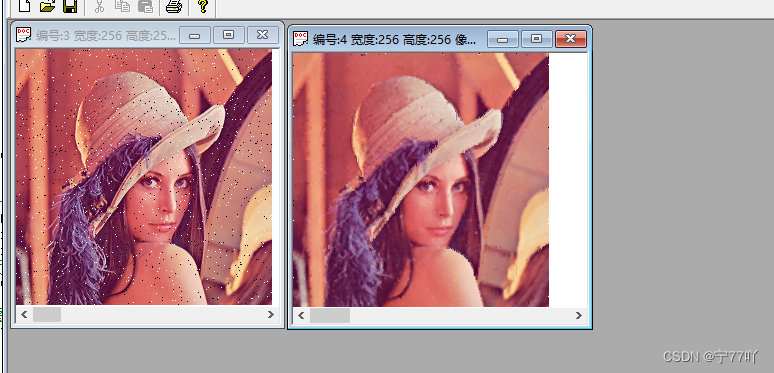
在这里插入图片描述

左：添加噪声的灰度图
右：使用矢量中值滤波算法后

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1280883.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

页面表格高度自适应

页面表格高度自适应

前言 现在后端管理系统主页面基本都是由三部分组成 查询条件&#xff0c;高度不固定&#xff0c;可能有的页面查询条件多&#xff0c;有的少表格&#xff0c;高度不固定&#xff0c;占据页面剩余高度分页&#xff0c;高度固定 这三部分加起来肯定是占满全屏的&#xff0c;那么我…
阅读更多...
openEuler学习05-ssh升级到openssh-9.5p1

openEuler学习05-ssh升级到openssh-9.5p1

openEuler的版本是openEuler 20.03&#xff0c;ssh的版本是OpenSSH_8.2p1 [roottest ~]# more /etc/os-release NAME"openEuler" VERSION"20.03 (LTS-SP3)" ID"openEuler" VERSION_ID"20.03" PRETTY_NAME"openEuler 20.03 (LTS-…
阅读更多...
Python安装步骤介绍

Python安装步骤介绍

本文将介绍Python安装的详细步骤如下&#xff1a; 下载 python安装 python配置环境变量&#xff08;安装时勾选配置环境变量的则无需此步骤&#xff09; 一、python下载 官网&#xff1a;Download Python | Python.org 根据电脑位数下载所需的版本 二、Python安装 1.打开安…
阅读更多...
基于深度学习面向中医诊断的舌象图像分割系统

基于深度学习面向中医诊断的舌象图像分割系统

1.研究背景与意义 项目参考AAAI Association for the Advancement of Artificial Intelligence 研究背景与意义 中医舌诊是通过观察舌的各种特征来了解人体的健康状况&#xff0c;从而对各种疾病做出诊断及病情评估&#xff0c;是传统中国医学应用最广、最有价值的诊法之一。…
阅读更多...
[C/C++]数据结构 关于二叉树的OJ题(利用分治思想解决难题)

[C/C++]数据结构 关于二叉树的OJ题(利用分治思想解决难题)

题目一: 单值二叉树 &#x1f6a9;⛲&#x1f31f;⚡&#x1f966;&#x1f4ac; &#x1f6a9;题目链接:力扣&#xff08;LeetCode&#xff09;官网 - 全球极客挚爱的技术成长平台 ⛲题目描述: 如果二叉树每个节点都具有相同的值&#xff0c;那么该二叉树就是单值二叉树。…
阅读更多...
每日一题：LeetCode-209. 长度最小的子数组（滑动窗口）

每日一题：LeetCode-209. 长度最小的子数组（滑动窗口）

每日一题系列&#xff08;day 11&#xff09; 前言&#xff1a; &#x1f308; &#x1f308; &#x1f308; &#x1f308; &#x1f308; &#x1f308; &#x1f308; &#x1f308; &#x1f308; &#x1f308; &#x1f308; &#x1f308; &#x1f308; &#x1f50e…
阅读更多...
一文弄懂BFS【广度优先搜索(Breadth-First Search)】

一文弄懂BFS【广度优先搜索(Breadth-First Search)】

BFS&#xff0c;全名为广度优先搜索(Breadth-First Search)&#xff0c;是一种用于图或树的遍历或搜索的算法。它的主要思想是由节点自身开始向它的邻居节点新进展开搜索&#xff0c;因此也常被形象地称为“层序遍历”。 BFS 基本思想 BFS 工作原理是&#xff0c;从开始节点开…
阅读更多...
shell命令编写

shell命令编写

1. 1 #!/bin/bash 2 3 directory_path"/txh"4 5 # 使用 find 命令查找指定路径下的文件&#xff0c;并使用 wc 命令统计行数&#xff08;即文件个数&#xff09;6 7 file_count$(find "directory_path" -type f | wc -l)8 9 10 echo "在路径$director…
阅读更多...
Wireshark 协议插件Lua开发 -数据包内嵌协议的解释

Wireshark 协议插件Lua开发 -数据包内嵌协议的解释

概述 因为公司项目涉及的协议打包&#xff0c;协议包内又嵌了一层IP包的奇葩套娃结构&#xff0c;为了方便抓包调试&#xff0c;利用Wireshark的协议插件开发功能&#xff0c;写了一个插件&#xff0c;博文记录以备忘。 环境信息 Wireshark 4.0.3 协议结构体套娃图 插件安装…
阅读更多...
Prime 1.0

Prime 1.0

信息收集 存活主机探测 arp-scan -l 或者利用nmap nmap -sT --min-rate 10000 192.168.217.133 -oA ./hosts 可以看到存活主机IP地址为&#xff1a;192.168.217.134 端口探测 nmap -sT -p- 192.168.217.134 -oA ./ports UDP端口探测 详细服务等信息探测 开放端口22&#x…
阅读更多...
轻盈悦耳的运动型气传导耳机，还有条夜跑灯，哈氪聆光体验

轻盈悦耳的运动型气传导耳机，还有条夜跑灯，哈氪聆光体验

我平时出门不管是散步、骑行&#xff0c;还是坐公交的时候&#xff0c;都喜欢戴上耳机听音乐&#xff0c;这可以让我放松心情。现在市面上的耳机还是以真无线为主&#xff0c;选择虽多&#xff0c;但不适合户外使用&#xff0c;听不见外界的声音&#xff0c;运动时还容易脱落&a…
阅读更多...
软件工程单选多选补充

软件工程单选多选补充

2. 4. 5. 6. 7. 8. 9. 10. 12。 13.
阅读更多...
软件设计模式原则（三）单一职责原则

软件设计模式原则（三）单一职责原则

单一职责原则&#xff08;SRP&#xff09;又称单一功能原则。它规定一个类应该只有一个发生变化的原因。所谓职责是指类变化的原因。如果一个类有多于一个的动机被改变&#xff0c;那么这个类就具有多于一个的职责。而单一职责原则就是指一个类或者模块应该有且只有一个改变的原…
阅读更多...
锁表的原因及解决办法

锁表的原因及解决办法

引言 作为开发人员&#xff0c;我们经常会和数据库打交道。 当我们对数据库进行修改操作的时候&#xff0c;例如添加字段&#xff0c;更新记录等&#xff0c;没有正确评估该表在这一时刻的使用频率&#xff0c;直接进行修改&#xff0c;致使修改操作长时间无法响应&#xff0…
阅读更多...
【【Micro Blaze 的 最后补充 与 回顾 】】

【【Micro Blaze 的 最后补充 与 回顾 】】

Micro Blaze 的 最后补充 与 回顾 Micro Blaze 最小系统 以 MicroBlaze 为核心、LocalMemory&#xff08;片上存储&#xff09;为内存&#xff0c;加上传输信息使用的 UART串口就构成了嵌入式最小系统。当程序比较简单时&#xff0c;Local Memory 可以作为程序的运行空间以及…
阅读更多...
OCR原理解析

OCR原理解析

目录 1.概述 2.应用场景 3.发展历史 4.基于传统算法的OCR技术原理 4.1 图像预处理 4.1.1 灰度化 4.1.2 二值化 4.1.3 去噪 4.1.4 倾斜检测与校正 4.1.4.2 轮廓矫正 4.1.5 透视矫正 4.2 版面分析 4.2.1 连通域检测文本 4.2.2 MSER检测文本 4.3 字符切割 4.3.1 连…
阅读更多...
Excel 分列功能

Excel 分列功能

一. 需求 ⏹有一段文本&#xff0c;文本一共有7列。这7列文本之间的分隔符不相同 有一个空格的有多个空格的有Tab的jmw_state 和 method 之间用 & 连接 现在要求&#xff0c;将这段文本粘贴到Excel中&#xff0c;进行分列。并且需要将 jmw_state 和 method 也进行分列 也…
阅读更多...
LASSO vs GridSearchCV

LASSO vs GridSearchCV

LASSO VS GridSearchCV LASSO定义目的使用方法原理示例总结 GridSearchCV定义目的使用方法原理网格搜索&#xff08;Grid Search&#xff09;交叉验证&#xff08;Cross-Validation&#xff09;总结 示例总结 总结 LASSO 定义 LASSO&#xff08;Least Absolute Shrinkage and…
阅读更多...
机器人阻抗控制性能及其实验验证

机器人阻抗控制性能及其实验验证

Impedance Control 机器人阻抗控制是一种控制方法&#xff0c;其目的是构建一个系统使得执行器&#xff08;如机械臂&#xff09;能同时控制力和位置。它基于阻抗模型&#xff0c;通过调节机器人的行为&#xff0c;以维持理想的动态关系。这种动态关系可以理解为机器人末端位置…
阅读更多...
【微信小程序】上传头像 微信小程序内接小程序客服

【微信小程序】上传头像 微信小程序内接小程序客服

这里写目录标题 微信小程序上传头像使用button按钮包裹img 微信小程序内接小程序客服使用button按钮跳转客服 微信小程序上传头像 使用button按钮包裹img 原本思路是只使用image标签再加上chooseImg&#xff0c;但发现使用button标签上传头像这种方法更实用。微信小程序文档上…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023