文章解读与仿真程序复现思路——电网技术EI\CSCD\北大核心《余电上网/制氢方式下微电网系统全生命周期经济性评估》

该标题涉及到对微电网系统的全生命周期经济性进行评估，其重点关注两种运营方式：余电上网和制氢。以下是对标题的解读：

微电网系统： 微电网是指一种小规模的电力系统，通常包括分布式能源资源（如太阳能、风能、蓄电池等）以及能源管理系统，能够在本地区域内生成、分配和管理电力。
余电上网方式： 这可能指微电网系统中的一种运营模式，其中系统产生的额外电力（余电）被注入到公共电网中，可能以出售的形式供其他用户使用。这种方式通常考虑了微电网系统与电网的互联。
制氢方式： 另一种微电网系统的运营模式，可能是将余电用于水电解产生氢气。制氢可以作为一种能量存储手段，将电能转化为氢气，以后再利用氢气产生电力。
全生命周期经济性评估： 这表示对微电网系统从建设、运营到报废的整个生命周期进行经济性评估。这可能包括了投资成本、运营维护成本、能源产出收益、以及可能的环境影响等因素。全生命周期经济性评估有助于综合考虑系统在长期内的经济效益。

综合起来，该标题表明研究的重点是在微电网系统中，通过余电上网和制氢两种方式，对系统的整个生命周期进行经济性评估。这种评估可以为决策者提供关于微电网系统部署和运营的经济效益信息，有助于制定合理的能源管理和经济决策。

摘要：为全面评估微电网系统不同运营方式下的经济性,从全社会角度出发,综合分析余电上网和余电制氢2种运营方式下微电网系统的成本和效益。考虑到不同类型、不同容量的分布式电源对微网系统各方面性能的影响,首先对微电网中的分布式电源定容问题进行研究。在满足具体约束的前提下,以全生命周期综合收益最大为目标函数,建立微电网系统双层优化模型。该双层优化模型上层优化采用自适应粒子群算法求解系统最优配置,下层优化采用CPLEX求解器求解上层配置方案下的最优调度方案。在此基础上,运用所建全寿命周期经济性评估模型,对具体算例最优配置下各成本和收益以及自平衡率进行对比分析,并得出余电制氢计划这一运营方式更具经济性的结论。

这段摘要描述了一项研究，旨在评估微电网系统在不同运营方式下的经济性。下面是对摘要中内容的解读：

研究目的： 评估微电网系统中两种不同运营方式（余电上网和余电制氢）的经济效益。这种评估是从整个社会的角度出发，目的在于全面分析两种方式下微电网系统的成本和效益。
考虑因素： 考虑到不同类型和容量的分布式电源对微电网系统各方面性能的影响。这可能涉及到不同能源资源（如太阳能、风能等）的影响，以及它们在微网系统中的配置和管理。
定容问题： 首先研究了微电网系统中的分布式电源定容问题。这可能意味着确定在微电网系统中合适的电源容量和类型，以最大化系统效率和经济性。
建立双层优化模型： 为了实现全生命周期综合收益最大化，建立了微电网系统的双层优化模型。上层优化采用自适应粒子群算法来寻找系统最优配置，而下层优化则使用CPLEX求解器来解决上层配置下的最优调度方案。
全寿命周期经济性评估模型： 在最优配置的基础上，运用建立的全寿命周期经济性评估模型，对具体算例下最优配置的各种成本和收益以及自平衡率进行对比分析。
结论： 在对比分析后，得出了余电制氢计划作为一种运营方式更具经济性的结论。这表明在经过评估后，制氢方式可能在经济效益上更有优势。

总的来说，这项研究利用双层优化模型和全寿命周期经济性评估模型，从整体经济性角度探讨了微电网系统不同运营方式下的效益，并得出了在特定情况下制氢方式更具经济性的结论。

关键词:成本效益分析; 分布式电源容量配置:双层优化;自适应粒子群算法:余电制氢;

成本效益分析： 这是一种评估项目、计划或系统的经济性的方法。在这个上下文中，研究的焦点是微电网系统的两种运营方式（余电上网和余电制氢）的成本和效益。成本效益分析有助于确定特定决策或投资是否具有经济合理性，以及在经济层面上哪种选择更为优越。
分布式电源容量配置： 意味着确定微电网系统中分布式电源的合适容量和类型。这可能包括考虑不同能源来源（如太阳能、风能等）的影响，以及它们在系统中的配置。在这个上下文中，分布式电源容量配置可能是优化系统性能和经济性的一个关键因素。
双层优化： 这是一种优化问题的解决方法，其中问题被划分为两个层次。在这里，研究使用了双层优化模型，其中上层优化采用自适应粒子群算法来找到系统的最优配置，而下层优化使用CPLEX求解器来解决上层配置下的最优调度方案。这种层次化的方法通常用于处理复杂的优化问题。
自适应粒子群算法： 这是一种进化算法，用于解决优化问题。粒子群算法模拟鸟群或鱼群中个体的群体行为，通过在搜索空间中移动的粒子来表示潜在的解。自适应粒子群算法具有调整参数的能力，以更好地适应不同问题的特性，因此在寻找系统最优配置方面可能是一种有效的方法。
余电制氢： 这是一种运营方式，指的是在微电网系统中，当有多余的电力时将其用于制取氢气。这种方式可能在能源储存和后续利用方面具有优势，特别是考虑到氢气可以作为一种清洁能源进行存储和运输。

这些关键词的结合表明研究的主要内容是在微电网系统中，通过双层优化和自适应粒子群算法来进行成本效益分析，特别关注了两种运营方式下的分布式电源容量配置，以及余电制氢作为一种可能的经济运营方式。

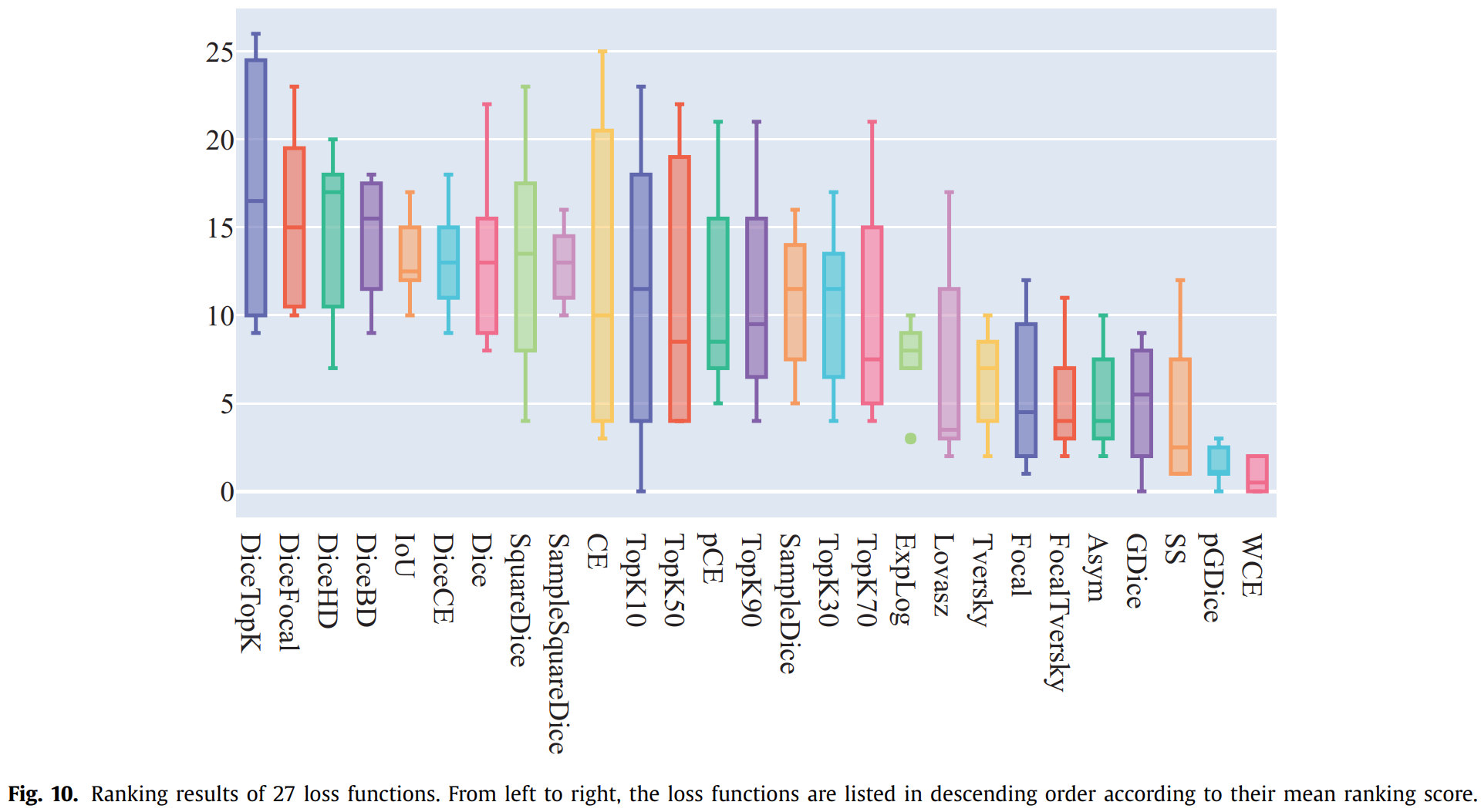
仿真算例：本文以西南某地区微电网为分析对象，算例中四季典型光伏和风电出力标幺值曲线以及该地区负荷曲线如附录 A 图 A1 所示。微电网生命周期为 20 年，折现率为 8%，单位 DG 额定容量、电量分别为 1kW、kW·h，各分布式电源所允许接入最大容量均为 10MW，微电网与外部电网交互允许最大功率为 2MW，自平衡率限制在 80%以上。微电网各设备对应的参数如附录 A 表 A1 所示[21-24]，不同发电类型产生的污染排放量及电力行业污染物环境评价标准相关数据分别见附录 A 表 A2、A3[23,25]。

仿真程序复现思路：

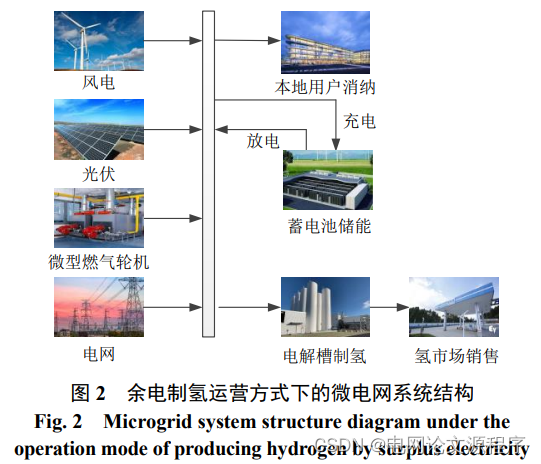
要复现上述仿真，我们需要考虑以下步骤和思路，并提供一个简化的示例代码，以Python语言为例。

import numpy as np

# 1. 定义光伏和风电出力标幺值曲线
solar_curve = np.array([0.2, 0.5, 0.8, 0.3, 0.1, 0.4, 0.7, 0.9, 0.6, 0.2, 0.1, 0.3])
wind_curve = np.array([0.3, 0.4, 0.6, 0.2, 0.1, 0.5, 0.7, 0.8, 0.4, 0.2, 0.1, 0.3])

# 2. 定义负荷曲线
load_curve = np.array([0.8, 0.7, 0.6, 0.5, 0.4, 0.6, 0.7, 0.9, 1.0, 0.8, 0.7, 0.6])

# 3. 初始化微电网参数
lifecycle = 20
discount_rate = 0.08
dg_capacity = 1
dg_energy = 1
max_capacity_per_source = 10
max_grid_interaction_power = 2
min_self_balance_rate = 0.8

# 4. 初始化设备参数
# 在这里，你需要根据具体情况替换下面的数值，并定义其他设备的参数
generator_parameters = {
    'parameter1': value1,
    'parameter2': value2,
    # ...
}

# 5. 粒子群算法的实现
def particle_swarm_optimization(num_particles=10, max_iterations=100, inertia=0.7, c1=1.5, c2=1.5):
    dimensions = len(generator_parameters)  # 粒子的维度，即变量的数量
    particles = np.random.rand(num_particles, dimensions)  # 随机初始化粒子群

    # 初始化粒子的速度
    velocities = np.zeros((num_particles, dimensions))

    # 初始化全局最优解
    global_best_solution = None
    global_best_fitness = float('inf')

    for iteration in range(max_iterations):
        for i in range(num_particles):
            # 计算当前粒子的适应度值
            current_fitness = fitness_function(particles[i])

            # 更新个体最优解
            if current_fitness < fitness_function(global_best_solution):
                global_best_solution = particles[i].copy()

            # 更新全局最优解
            if current_fitness < global_best_fitness:
                global_best_fitness = current_fitness

            # 更新粒子的速度和位置
            velocities[i] = inertia * velocities[i] + c1 * np.random.rand() * (global_best_solution - particles[i]) + c2 * np.random.rand() * (global_best_solution - particles[i])
            particles[i] = particles[i] + velocities[i]

    return global_best_solution

# 6. 定义适应度函数
def fitness_function(solution):
    # 在这里计算适应度，可以是成本、效益等的函数
    # 使用上述定义的各种数据和参数
    # 返回适应度值
    pass

# 7. 运行粒子群算法进行微电网系统优化
optimized_solution = particle_swarm_optimization()

# 输出优化结果
print("Optimized Solution:", optimized_solution)

请注意，这只是一个简化的例子，真实的微电网仿真程序可能需要更多的考虑和更复杂的模型。适应度函数的设计取决于你的优化目标，可能需要考虑微电网的经济性、可靠性等因素。在实际应用中，你可能还需要考虑更多的约束条件和问题特定的参数。