【动态规划】LeetCode-面试题 17.16. 按摩师

news2025/1/19 3:00:11

🎈算法那些事专栏说明：这是一个记录刷题日常的专栏，每个文章标题前都会写明这道题使用的算法。专栏每日计划至少更新1道题目，在这立下Flag🚩
🏠个人主页：Jammingpro
📕专栏链接：算法那些事
🎯每日学习一点点，技术累计看得见

题目

题目描述

一个有名的按摩师会收到源源不断的预约请求，每个预约都可以选择接或不接。在每次预约服务之间要有休息时间，因此她不能接受相邻的预约。给定一个预约请求序列，替按摩师找到最优的预约集合（总预约时间最长），返回总的分钟数。

执行示例

示例 1：
输入： [1,2,3,1]
输出： 4
解释：选择 1 号预约和 3 号预约，总时长 = 1 + 3 = 4。

示例2：
输入： [2,7,9,3,1]
输出： 12
解释：选择 1 号预约、 3 号预约和 5 号预约，总时长 = 2 + 9 + 1 = 12。

示例3：
输入： [2,1,4,5,3,1,1,3]
输出： 12
解释：选择 1 号预约、 3 号预约、 5 号预约和 8 号预约，总时长 = 2 + 4 + 3 + 3 = 12。

题解

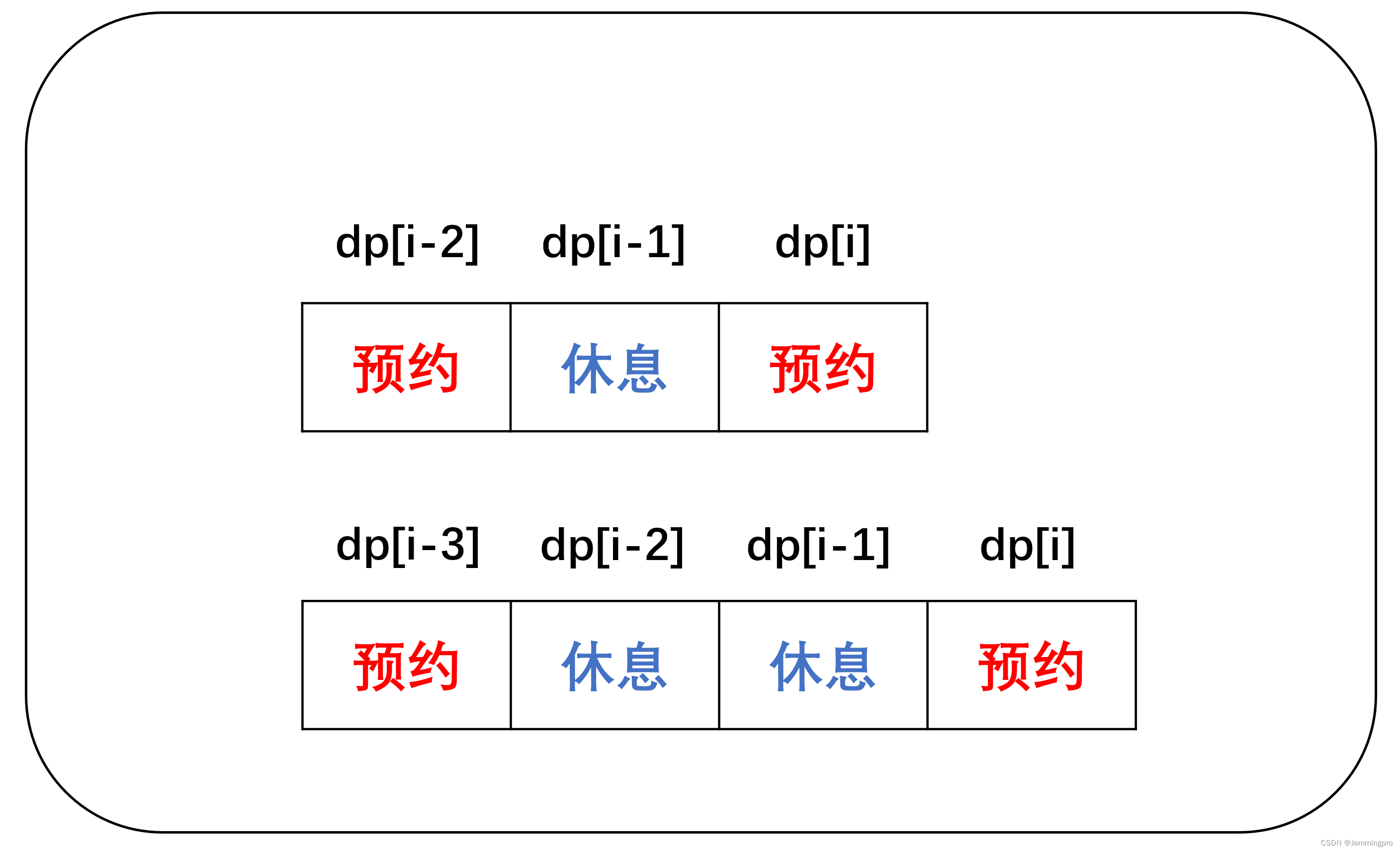
由题意可知，按摩师无法接受相邻的预约，因而只有以下几种方式满足预约要求：①一次预约一次休息，预约与休息交替、②一次预约后，休息两次再预约。如下图所示↓↓↓
在这里插入图片描述
以上两种方式是预约最为紧凑的两种方式，那为什么没有预约一次后休息3次及以上呢？因为3次及以上休息中的可以将其中的部分休息时间改为预约，这样可以使得总的预约时长更大。而两次休息和一次休息中间没有任何一次休息可以改为预约。如下图所示↓↓↓
在这里插入图片描述
针对于上面两种预约方式，如果还不理解为什么一定要考虑"1预约后休息2次"的话，请看下面的例子：若有预约时长序列为[100,1,1,100,1,1,100]的情况，则我们按照预约1次休息1次的预约方式，则其得出的结果如下图所示↓↓↓
在这里插入图片描述
第一个表格显示的是预约时长序列，第二和第三个表示表示的是休息与预约交替的预约方式，它们均没有求出最长预约时长，而预约1次休息2次的方式可得到最长预约时长。因此，这两种预约方式我们都要考虑。

设预约时长序列为nums，我们创建一个dp表（一维数组）来存储到达第i个时长序列（下标为i的时长序列）时累计的最大预约时长。计算dp[i]时，说明第i个时间序列为预约状态，则我们不能将i-1设置为预约状态，但我们可以将i-2和i-3设置为预约状态（i-2设置为预约状态就是"休息-预约"交替进行的预约模式，i-3设置为预约状态就是"预约1次预约2次的休息方式"）。我们可以得到dp[i]=max(dp[i-2], dp[i-3])+nums[i]。将i设置为预约状态和将i-1设置为预约状态，两者是互斥的。可能将上一步设置为预约状态会比将当前位置为预约状态的累计预约时长更大，因此，我们还需要执行dp[i]=max(dp[i],dp[i-1])。
在这里插入图片描述
经过上面的分析，我们可以得到如下代码↓↓↓

class Solution {
public:
    int massage(vector<int>& nums) {
        int n = nums.size();
        vector<int>dp(n);
        if(n == 0) return 0;
        if(n == 1) return nums[0];
        if(n == 2) return max(nums[0], nums[1]);
        dp[0] = nums[0];
        dp[1] = nums[1];
        dp[2] = max(dp[1], dp[0] + nums[2]);
        for(int i = 3; i < n; i++)
        {
            dp[i] = max(dp[i - 2], dp[i - 3]) + nums[i];
            dp[i] = max(dp[i], dp[i - 1]);
        }
        return dp[n - 1];
    }
};

除了这种思路外，我们还可以创建两个一维数组，分别命名为f和g，f数组存储当前位置为预约状态时累计的最长预约时长，g数组存储的时当前位置为休息状态时累计的最长预约时长。我们可以得到以下两个状态转移方程（递推公式）：f[i]=g[i-1]+nums[i]（）和g[i]=max(g[i-1],f[i-1])

ps：f[i]状态转移方程解释->已经知道上一个位置设置为休息状态时的最大累计预约时长，只要加上当前下标的时间序列即可。

ps：g[i]状态转移方程解释->当前为休息状态，上一个位置可以是休息也可以是预约，从两者中选择最大的，就能保证当前位置的累计预约时长最大。其实现代码如下↓↓↓

class Solution {
public:
    int massage(vector<int>& nums) {
        int n = nums.size();
        if(n == 0)
            return 0;
        vector<int>f(n);
        vector<int>g(n);
        f[0] = nums[0];
        for(int i = 1; i < n; i++)
        {
            f[i] = g[i - 1] + nums[i];
            g[i] = max(f[i - 1], g[i - 1]);
        }
        return max(f[n - 1], g[n - 1]);
    }
};