目前已经可以画出单个三角形了，那么多个三角形的可见性或遮挡问题如何解决（解决先后向问题）？

1.深度缓冲Z-buffering

1.画家算法：先把远处的东西画在屏幕上，再画近处的，从而近处物体覆盖远处物体。（油画家）

但是当用这个算法去画一个立体正方形时，会出现后面的边显示出来的错误效果。

所以我们引入了深度缓冲。

2.深度缓冲

这是一个在图形学中广泛采用的算法

假设在深度测试中离我们越近的物体深度值越小，越远的物体深度值越大。

• Store current min. z-value for each sample (pixel) 存储每个样本当前最小的深度值（以像素为单位）
• Needs an additional buffer for depth values 需要额外的深度值缓冲区
- frame buffer stores color values 帧缓冲区存储颜色值
- depth buffer (z-buffer) stores depth 深度缓冲区存储深度

基本思想：每一个像素内记录它的最浅深度，对于任意一个三角形都可以把它光栅化成不同的像素，所以我们就可以找到任意一个三角形覆盖的任意一个像素

算法流程：

1.首先认为所有深度缓存中的所有像素一开始记录的距离或者深度都是无限远的（R）

2.然后我们把一个个三角形以任何的顺序往里面做rasterization（光栅化）

3.如果当前三角形像素的深度小于之前记录的最小三角形深度，就替换掉

使用深度缓存的案例：只记录深度值最小的像素点

算法复杂度：运算n个三角形的复杂的为O（n）

为什么是线性的复杂度？因为我们始终只是在记录最小值，并没有排序。

有一个问题：当两个三角形有深度值相同的像素点时怎么办？一般浮点数运算很难有相同的，然后万一出现相同值的话，后面会再讲。此外深度缓存也无法处理透明物体，透明物体后面也需要特殊处理。

2.Shading着色

1.我们目前学了哪些知识

我们现在已经学会了MVP变换，也学会了光栅化。

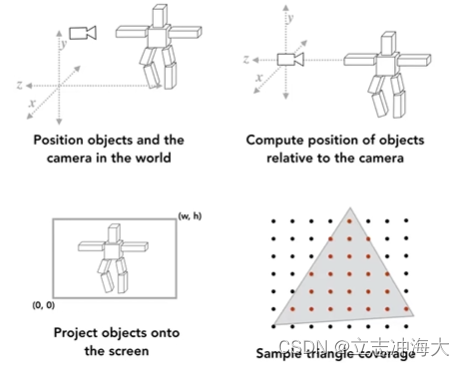
我们知道，其实将一个物体渲染的步骤无非以下：

1.把模型放好（给出模型中各个点的坐标）
2.把相机放好（把相机摆到标准位置）
3.对着模型拍一张照片（视图变换，投影变换以及视口变换）
4.在屏幕上画出这张照片（光栅化）

总而言之，所谓渲染，其实就是照照片。只不过这个照片是电脑画出来的

总结来讲我们目前所学知识还不能表现物体的明暗变化。

2.定义

The darkening or coloring（明暗与颜色） of an illustration or diagram with parallel lines or a block of color.

在图形学中的定义：The process of applying a material to an object. 对不同物体应用不同材质的过程叫做着色。

3.一个基础的着色模型：Blinn-Phong Reflectance Model

现在考虑的光照是考虑在任何一个点上，假设看到的这个点叫shading point，考虑这个点的着色结果是什么。

shading point是在一个物体表面上，物体表面可以是曲面，我们认为在一个局部的一个非常小的范围内，它永远是一个平面。

n是平面的法线，也就是垂直这个平面的一个方向

v是观测方向，也就是朝向相机的方向

l是光照方向，光射过来的方向

表面的其他参数，例如颜色、光泽…

以上表示方向的都是单位向量，只表示方向，长度永远为1

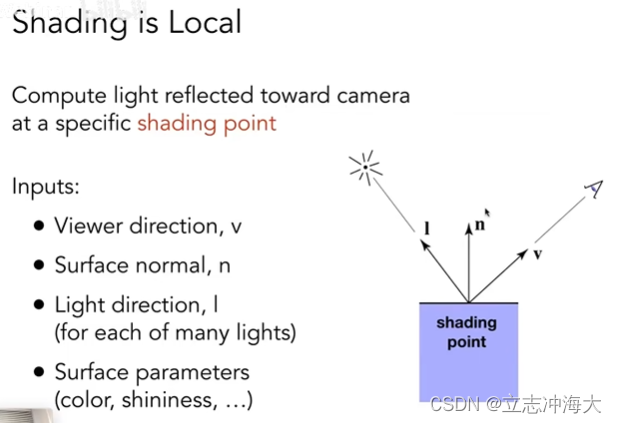
着色是局部的，既不会生成阴影，不考虑其他物体的存在，只考虑这个点自己。

下面我们要分别处理高光、漫反射和环境光。

3.漫反射

对于漫反射，我们需要考虑两方面的因素：

• 入射角度
• 距离

1.入射角度对漫反射的影响

先说为什么和入射角度相关。

我们先取一小块单位表面。

当光直射表面的时候，接收光照的面积是整个面积，即1。
当光与表面有一个夹角的时候（我们用表面法向n与入射光I的夹角theta表示），接收光照的面积只是一部分面积。即小于1。
当光与表面完全平行的时候（也就是theta=90°），接收光照的面积为0。
那么具体来说，假如成theta角，接收光照的面积是原来的多少呢？

答案是cos ⁡ θ

可以画出如下面第三个图来推导。

显然下面的那块面积正是1 ⋅ cos ⁡ θ

而由于采用了单位向量，恰好单位向量I与n之间的点积就是cos ⁡ θ

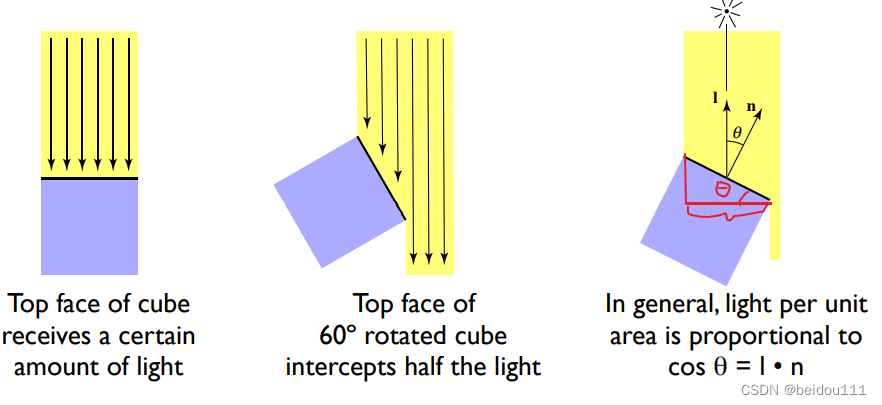
我们可以认为，只有cos ⁡ θ的光能量被表面接收了。所以自然亮度要乘以cos ⁡ θ 。

2.距离对漫反射的影响

另一个影响因素，是距离

对于一个点光源来说，我们想象光向外发射出一个球壳。由于能量守恒的缘故，显然这个球壳越大，能量就约稀薄。也就是单位面积上能够接收到的能量就越小。这和摊煎饼是一个道理，摊的越大，面糊糊越薄。

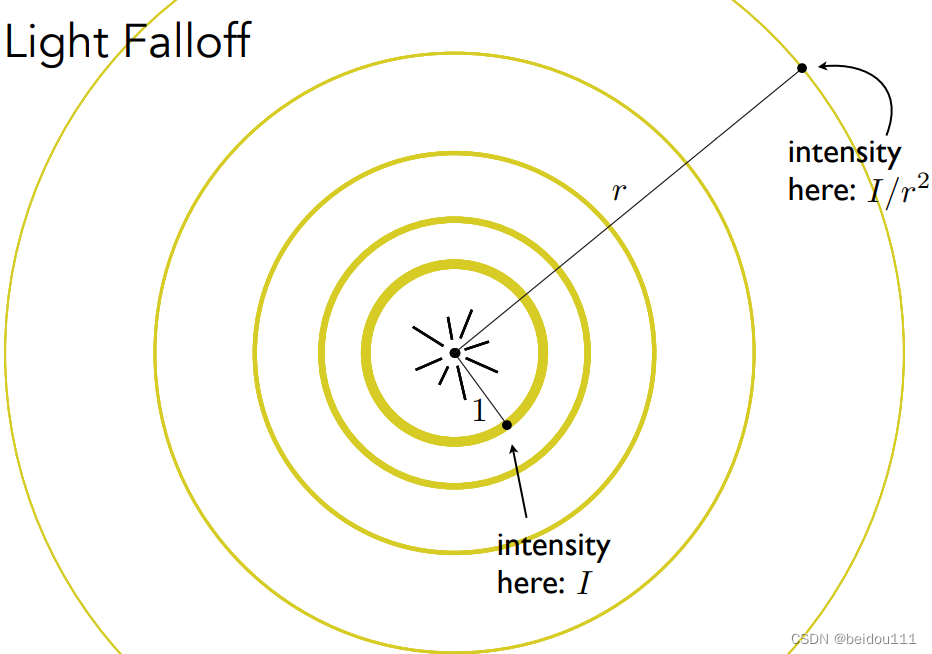
按照什么样的比例衰减呢？

自然是球壳表面积有多大，能量就要均摊多少！

球壳表面积是4 π r ^2

所以光的能量自然是按照r^2这个比率来衰减的了！

3.Lambertian 定律

把上述两点因素结合起来，我们就得到了漫反射的规律，这被称之为Lambertian 定律。

就是下面这个公式

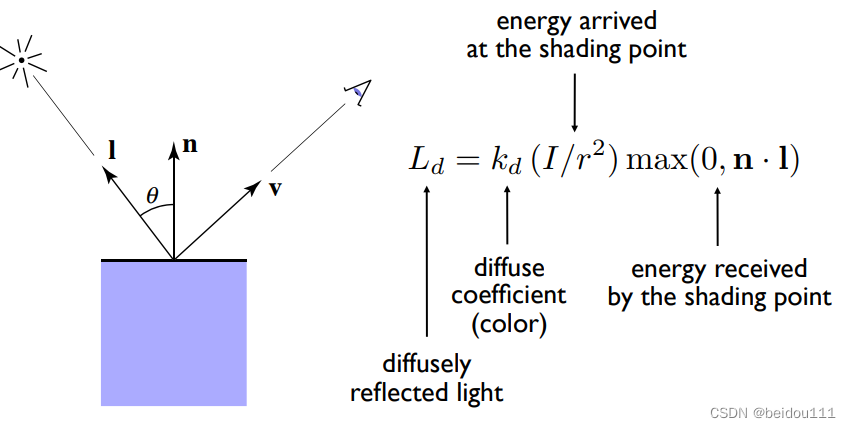
这里要说明：

为什么要用max(0, …)?
这是为了防止出现负数。而在我们情况里，夹角出现负数是没有意义的。光线不可能从物体的内部照射到物体表面。
为什么要有前面的系数kd?
首先，我们可以通过这个系数调整漫反射的强度，也就是明暗。其次，假如我们把它设置为向量，还可以表示不同颜色。因为不同颜色的吸收率可能是不同的。我们对每个颜色（RGB）给出一个系数，用来表示这种颜色没有被吸收的占比。这样就可以造成不同颜色的漫反射效果。
为什么没有视线向量v？
是因为漫反射与视角无关。无论你从哪个方向看过去，漫反射的光都是一样的。所以这个公式和v没有任何的关系。

下图展示了左上方光源照射一个球体得到的漫反射图像。可以发现：球体右下部分由于与光线夹角为0，是无法接受光线的，所以是暗的。而随着往左上方，球体表面法向与光源夹角越来越小，所以越来越亮。

不同的图片表示了不同kd的结果。这也可以看出，kd可以调整漫反射的强度。如果kd是1表明这个点完全不吸收能量，将能量反射出去，它是最亮的，如果是0表明这个表面是黑的，光线打到他后所有的能量都被吸收了，没有能量反射出去。kd可以使用一个rgb的向量表示

一句话：漫反射处理的是物体与光源的相对位置（远近和方向）所造成的明暗变化。

总结：从着色开始慢慢难起来了，后面这部分如果听不懂的话可以多听几遍，Lambertian 公式这里我听了4遍才逐渐掌握。