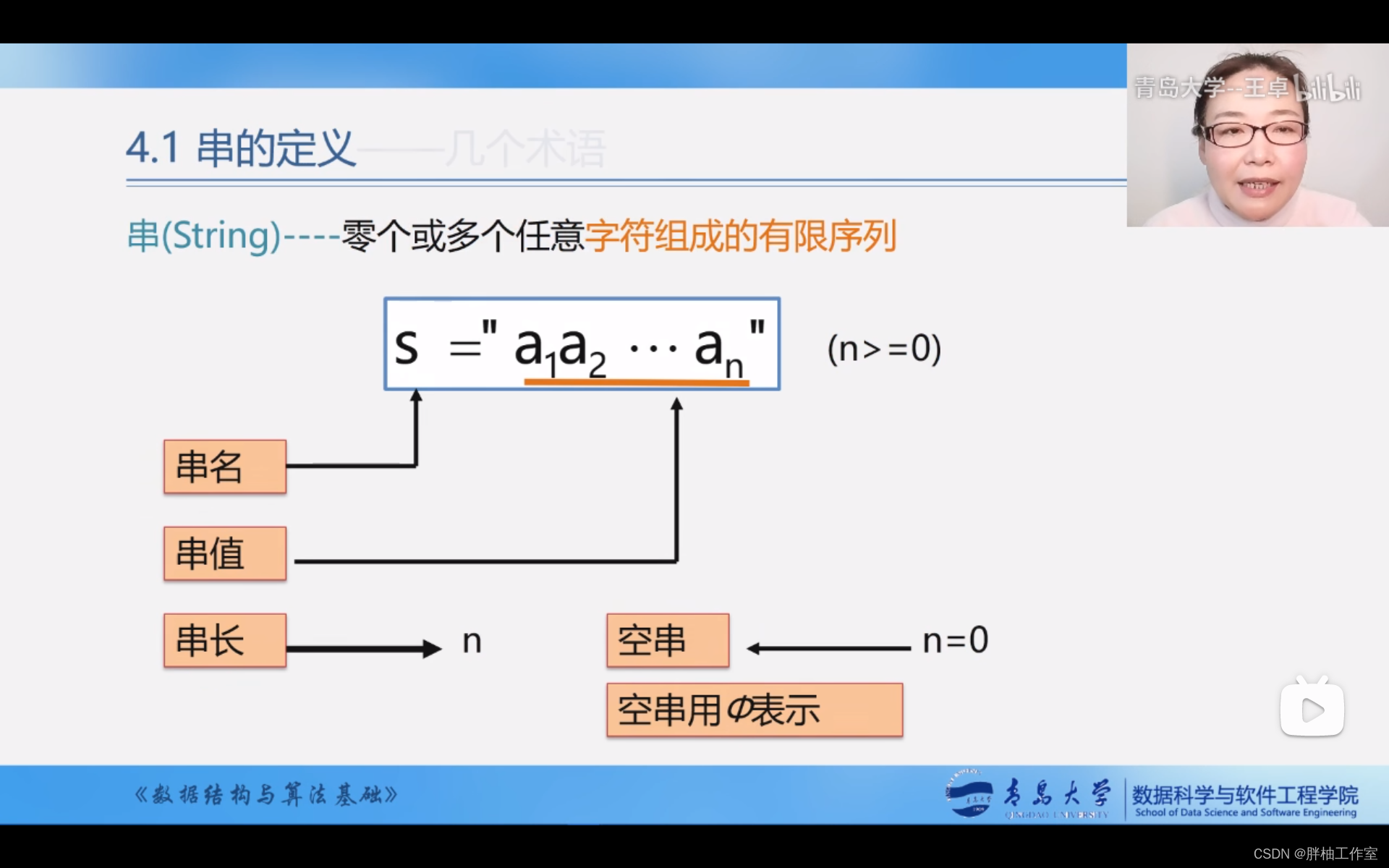
一、定义及常见术语

在这里插入图片描述

串相等：当两个串的长度相等且对应位置上的字符都相同时，这两个串才是相等的

所有的空串都是相等的

二、两种存储结构

2.1顺序存储结构（更常用）

#define MAXLEN 255
typedef struct {
    char ch[MAXLEN+1];//存储串的一维数组
    int length;//串的当前长度长度
} SString;

2.2 链式存储结构

#define CHUNKSIZE 80
typedef struct Chunk{
	char ch[CHUNKSIZE + 1];
	struct Chunk *next;
}Chunk;//串的结点类型

typedef struct {
	Chunk *head, *tail;//串的头、尾指针 
	int length;//串的当前长度 
}LString;//串的块链结构

三、模式匹配算法

目的：确定主串中所含字串 (模式串) 第一次出现的位置

应用：搜索引擎、拼写检查、语言翻译、数据压缩

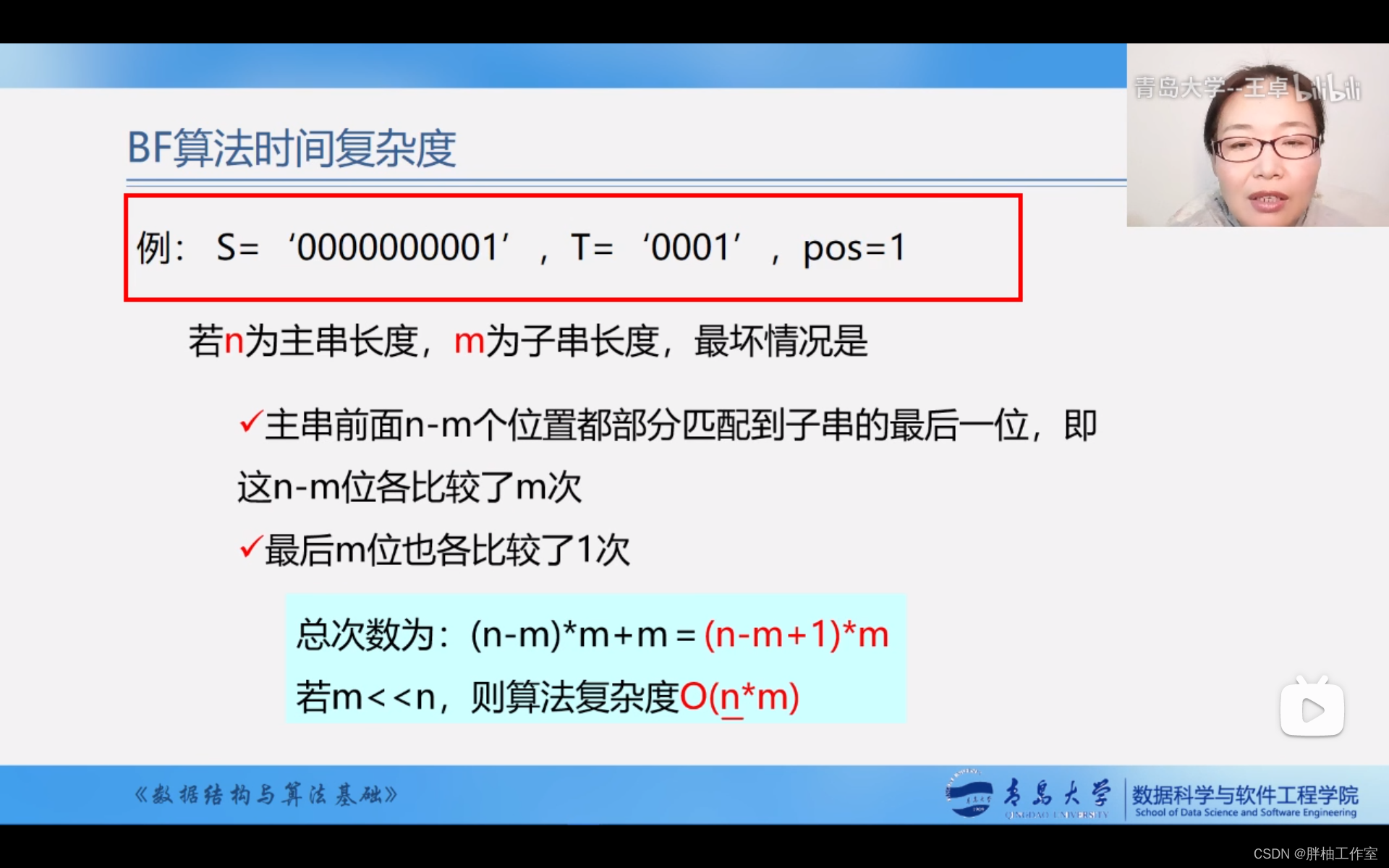
3.1 BF算法 (Brute-Force)

将主串的第pos个字符和模式串的第一个字符比较
若相等，继续逐个比较后续字符
若不等，从主串的下一字符开始，重新和模式串的第一个字符比较

int Index_BF(SString S, SString T, int pos) {
    int i = pos, j = 1;//为了方便描述，这里的sstring类的第零位置不储存元素
    while (i <= S.length && j <= T.length) {
    //若第一个不符合，则匹配失败；若第二个不符合，则匹配成功
        if (s.ch[i] == T.ch[j]) ++i, ++j;//主串和字串依次匹配下一个字符
        else {i = i-j+2; j = 1;} //回溯
        //i=i-j+2,理解为i-（j-1）+1。j从1到j走了j-1步，则i也走了j-1步。减j-1后再+1，是回到主串原来开始匹配的下一个位置
    }
    if (j > T.length) return i-T.length;
    else return 0; //模式匹配不成功
}
//主串长n，子串长m，时间复杂度O(n*m)，复杂度较高。

在这里插入图片描述

3.2 KMP算法

可参考：KMP算法易懂版

补充：包含首字母，不包含尾字母的所有子串都称为前缀，包含尾字母，不包含首字母的所有子串都称为后缀。
找最长的（长度小于比较指针左端子串长度的）公共前后缀
不需要看主串，只需要将模式串的相关信息提取出来之后就可以与任意的主串进行匹配。
公共前后缀的长度需小于比较指针左侧子串的长度
移动后，比较指针左侧子串的长度即为公共前后缀的长度
模式串的“最大公共前后缀长度+1”号位与主串当前位进行比较即可。

示例：
在这里插入图片描述

int Index_KMP(SString S, SString T, int pos) {
    int i = pos, j=1;
    while (i < S.length && j<=T.length) {
        if (j == 0 && S.ch[i] == T.ch[j]) ++i, ++j;
 //j == 0是因为当j退到0时，也就是主串的第i个字符与模式串的第一个字符不等时，应从主串的第i+1个字符重新与模式串的第一个字符作比较
        else j = next[j]; 
        //i不变，j后退，这里利用了一个next数组来存放j要飞到的位置，而不是每一次都从头开始
    }
    if (j > T.length) return i-T.length;//返回第一个字符的下标，匹配成功
    else return 0; //模式匹配不成功
}
 
void get_next(SString T, int &next[]) {//获得next数组，记录j的坐标位置
    i = 1; next[1] = 0; j = 0; 
	while (i < T.length) {
        if (j == 0 || T.ch[i] == T.ch[j]) {
            ++i; ++j;
            next[i] = j;
        }
        else j = next[j];
    } 
} 
//具体来说就是，j回溯改成，让模式串中模式匹配不成功位置之前的串中的最长前后缀的前缀到后缀位置，这样就推动了j的后移
//下图是示意图，其中next记录的是j可以飞到的位置，也就是最长公共前后缀的长度+1，注意最长前后缀的长度要小于不同位置之前串的长度才行！