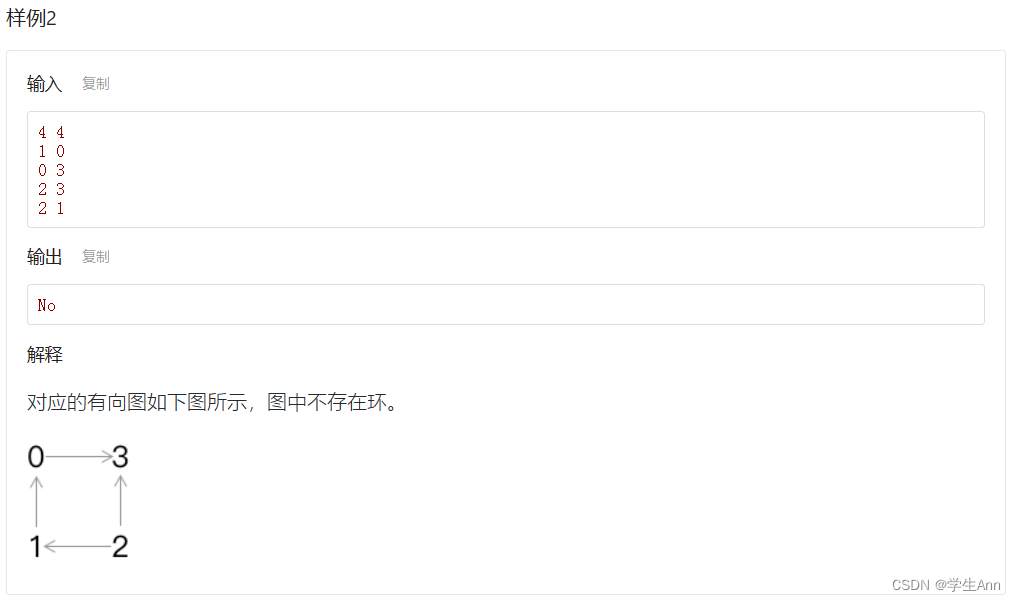
现有一个共n个顶点、m条边的有向图(假设顶点编号为从0到n-1),如果从图中一个顶点出发,沿着图中的有向边前进,最后能回到这个顶点,那么就称其为图中的一个环。判断图中是否有环。

解题思路:
判断是否为环,应该通过遍历图来看一次遍历是否所有结点都被遍历,如果是的话,说明构成一个环,特征为:遍历会回到最初的结点,否则不是。
由此可知,比无向图的判定多了一个回溯问题,因为我们不知道哪个是有向图的起始根结点。
于是在遍历时应该这么写:
bool dfs(int v){
isvisited[v] = true;
for(int i=0;i<map[v].size();i++){
int newv = map[v][i];
if(isvisited[newv]){
return true;
}
else{
if(dfs(newv){
return true;//如果成功是环,那么就不断返回递归true
}
}
}
isvisited[v] = false;
return false;//如果该根节点进入不构成环,那么每个访问过的都应该重新设置为false,并且返回false状态表示该结点无法构成环。
}
完整代码如下:
#include <iostream>
#include <vector>
using namespace std;
bool isvisited[100] = {false};
vector<int> map[100];
bool DFS(int v){
isvisited[v] = true;
for(int i=0;i<map[v].size();i++){
int newv = map[v][i];
if(isvisited[newv]==true){
return true;
}
else if(!isvisited[newv]){
if(DFS(newv)){
return true;
}
}
}
isvisited[v] = false;
return false;
}
int main(){
int n,m;
cin>>n>>m;
int a,b;
for(int i=0;i<m;i++){
cin>>a>>b;
map[a].push_back(b);
}
bool result = false;
for(int i=0;i<n;i++){
if(!isvisited[i]){
if(DFS(i)){
result = true;
}
}
}
printf(result?"Yes":"No");
return 0;
}