传统作业场景下电力设备的运维和维护都是人工来完成的,随着现代技术科技手段的不断发展,基于无人机航拍飞行的自动智能化电力设备问题检测成为了一种可行的手段,本文的核心内容就是基于YOLOv7来开发构建电力设备螺母缺销检测识别系统,首先看下实例效果:

简单看下数据集:


数据集均由无人机航拍进行采集。
这里有两个比较突出的问题,一方面是数据本身都是高分辨率的图像,另一方面是由于这里的检测对象都是非常小的目标,相较于整个图像的面积来说占比极小,对于模型的来说检测识别的难度是很高的。这里我尝试了基于原始的图像来直接开发构建检测模型,发现效果非常不理想,结合高分辨率和小目标这两个关键点,考虑对原始高分辨率图像进行切分处理,切分后数据如下:

简单的实现如下所示:
from PIL import Image
def split_image(image_path, tile_width, tile_height):
image = Image.open(image_path)
image_width, image_height = image.size
tiles = []
for y in range(0, image_height, tile_height):
for x in range(0, image_width, tile_width):
box = (x, y, x + tile_width, y + tile_height)
tile = image.crop(box)
tiles.append(tile)
return tiles
# 示例用法
image_path = "path/to/your/image.jpg"
tile_width = 100
tile_height = 100
sub_images = split_image(image_path, tile_width, tile_height)
for i, sub_image in enumerate(sub_images):
sub_image.save(f"sub_image_{i}.jpg")当然了也可以借助于一些其他工具模块,总之实现自己的目的即可,这里就不再赘述了。
下面以具体的实例来进行说明,实例测试图像如下所示:

切分结果如下所示:

接下来为了确认切分逻辑的正确性,我们依次读取切分得到的子图数据,来整体显示在一张图像上,如下所示:

可以看到是没有问题的,数据处理就到这里,接下来开始构建模型训练阶段。
训练数据配置文件如下所示:
# txt path
train: ./dataset/images/train
val: ./dataset/images/test
test: ./dataset/images/test
# number of classes
nc: 3
# class names
names: ['DefectPin', 'Nut', 'NormalPin']
这里一共开发构建了两款不同参数量级的模型,分别是yolov7-tiny和yolov7,接下来我们来整体对比分析模型的性能差异:
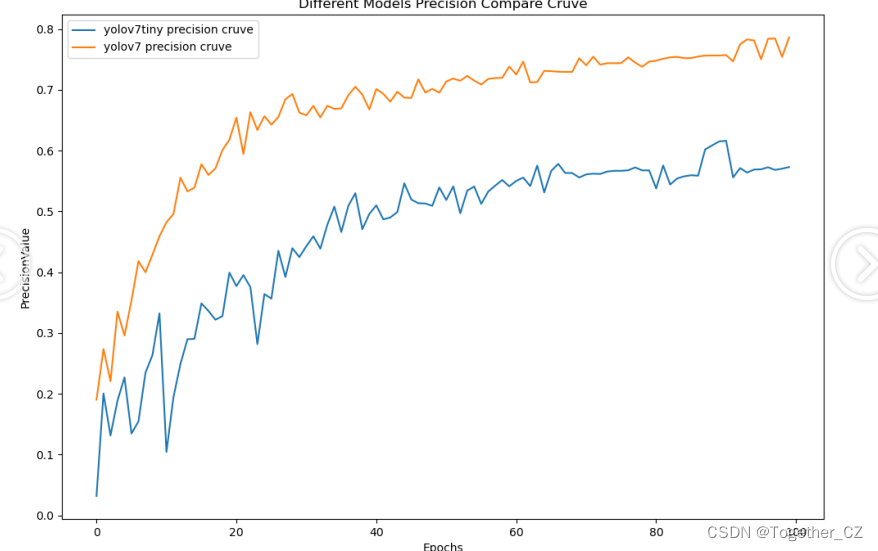
【Precision曲线】
精确率曲线(Precision-Recall Curve)是一种用于评估二分类模型在不同阈值下的精确率性能的可视化工具。它通过绘制不同阈值下的精确率和召回率之间的关系图来帮助我们了解模型在不同阈值下的表现。
精确率(Precision)是指被正确预测为正例的样本数占所有预测为正例的样本数的比例。召回率(Recall)是指被正确预测为正例的样本数占所有实际为正例的样本数的比例。
绘制精确率曲线的步骤如下:
使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
对于每个阈值,计算相应的精确率和召回率。
将每个阈值下的精确率和召回率绘制在同一个图表上,形成精确率曲线。
根据精确率曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
通过观察精确率曲线,我们可以根据需求确定最佳的阈值,以平衡精确率和召回率。较高的精确率意味着较少的误报,而较高的召回率则表示较少的漏报。根据具体的业务需求和成本权衡,可以在曲线上选择合适的操作点或阈值。
精确率曲线通常与召回率曲线(Recall Curve)一起使用,以提供更全面的分类器性能分析,并帮助评估和比较不同模型的性能。
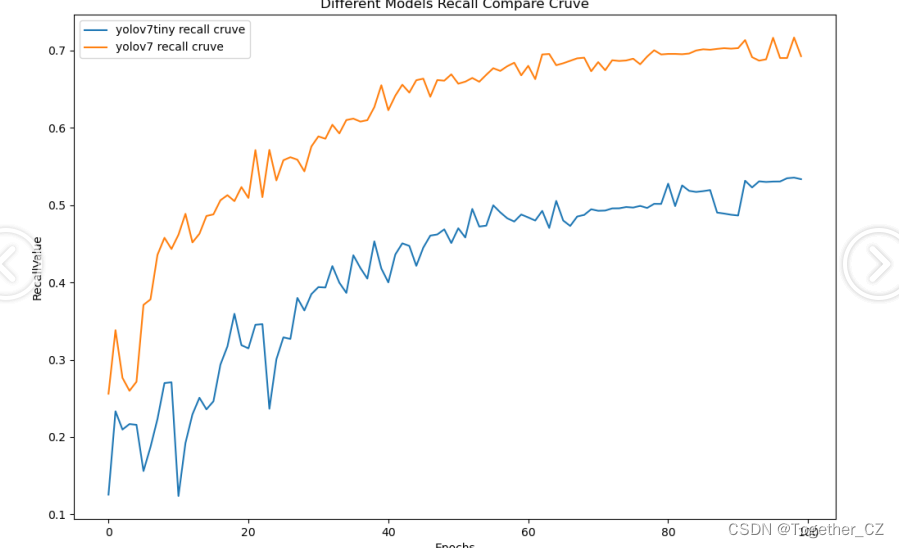
【Recall曲线】
召回率曲线(Recall Curve)是一种用于评估二分类模型在不同阈值下的召回率性能的可视化工具。它通过绘制不同阈值下的召回率和对应的精确率之间的关系图来帮助我们了解模型在不同阈值下的表现。
召回率(Recall)是指被正确预测为正例的样本数占所有实际为正例的样本数的比例。召回率也被称为灵敏度(Sensitivity)或真正例率(True Positive Rate)。
绘制召回率曲线的步骤如下:
使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
对于每个阈值,计算相应的召回率和对应的精确率。
将每个阈值下的召回率和精确率绘制在同一个图表上,形成召回率曲线。
根据召回率曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
通过观察召回率曲线,我们可以根据需求确定最佳的阈值,以平衡召回率和精确率。较高的召回率表示较少的漏报,而较高的精确率意味着较少的误报。根据具体的业务需求和成本权衡,可以在曲线上选择合适的操作点或阈值。
召回率曲线通常与精确率曲线(Precision Curve)一起使用,以提供更全面的分类器性能分析,并帮助评估和比较不同模型的性能。
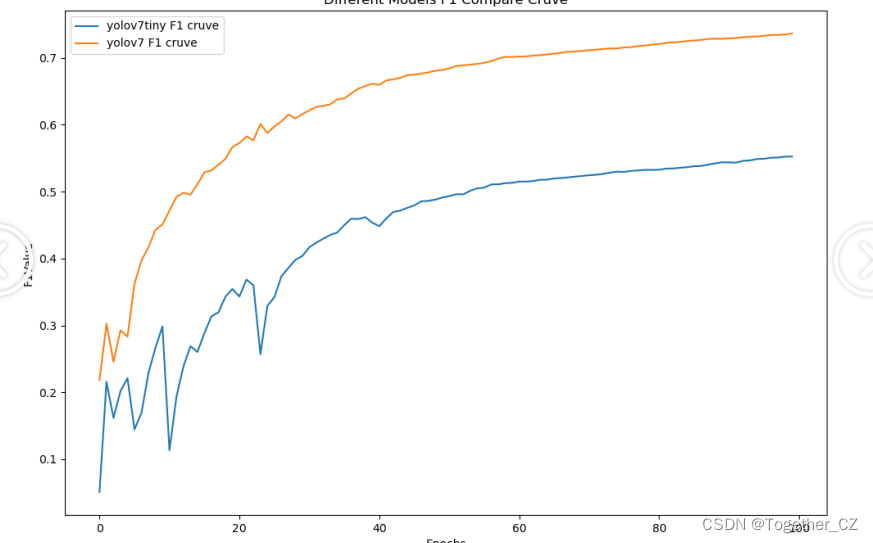
【F1值曲线】
F1值曲线是一种用于评估二分类模型在不同阈值下的性能的可视化工具。它通过绘制不同阈值下的精确率(Precision)、召回率(Recall)和F1分数的关系图来帮助我们理解模型的整体性能。
F1分数是精确率和召回率的调和平均值,它综合考虑了两者的性能指标。F1值曲线可以帮助我们确定在不同精确率和召回率之间找到一个平衡点,以选择最佳的阈值。
绘制F1值曲线的步骤如下:
使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
对于每个阈值,计算相应的精确率、召回率和F1分数。
将每个阈值下的精确率、召回率和F1分数绘制在同一个图表上,形成F1值曲线。
根据F1值曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
F1值曲线通常与接收者操作特征曲线(ROC曲线)一起使用,以帮助评估和比较不同模型的性能。它们提供了更全面的分类器性能分析,可以根据具体应用场景来选择合适的模型和阈值设置。
【loss对比】
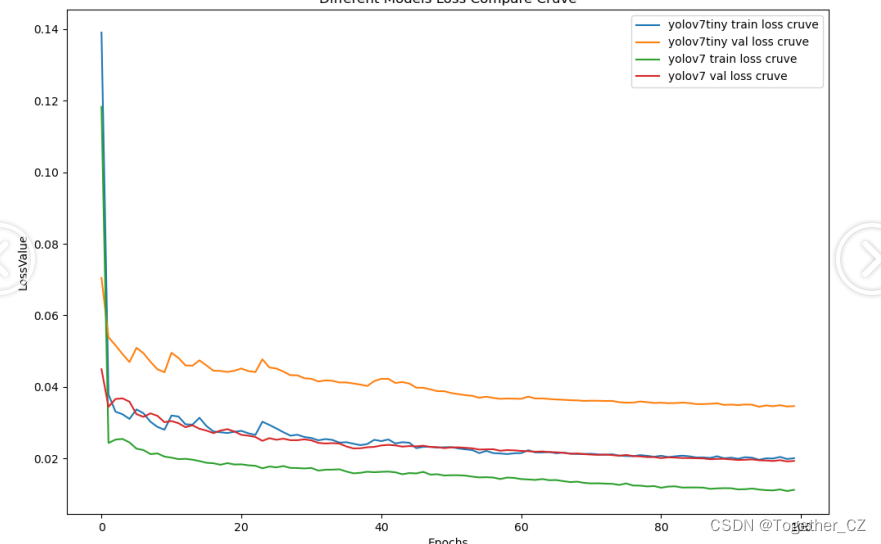
可以看到:在各个指标对比上yolov7全面碾压的态势超越yolov7-tiny。
接下来详细看下yolov7的结果详情:
【混淆矩阵】

【训练可视化】
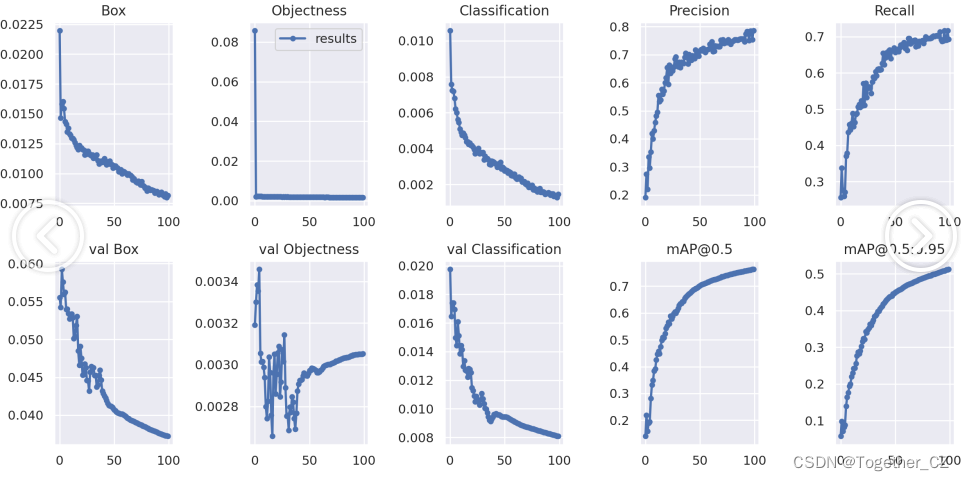
【Batch计算实例】


实例推理效果如下所示:

可以看到:目标对象区域非常非常的小,如果不仔细观察可能都会漏掉了。

感兴趣也都可以参照本文的建模处理思路来进行构建自己的模型,相信会有一定的收获。