参考书目:深入浅出Python量化交易实战
在机器学习里面的X叫做特征变量,在统计学里面叫做协变量也叫自变量,在量化投资里面则叫做因子,所谓多因子就是有很多的特征变量。
本次带来的就是多因子模型,并且使用的是机器学习的强大的非线性模型,集成学习里面的随机森林和LGBM模型,带来因子的选择策略和股票的选择策略。
由于股票数据的获取都需要第三方库或者是专业的量化投资框架,很多第三方库某些功能需要收费(Tushare),而免费的一些库(证券宝)获取的数据特征变量又没那么多。所以这里是用聚宽量化投资框架,是可以免费使用一些功能的(只需要注册一个账号)。这里获取数据就采用聚宽平台的功能了。
数据获取
本次使用沪深300作为股票池,选获取一些财务指标:
#创建query对象,指定获取股票的代码、市值、净运营资本
#净债务、产权比率、股东权益比率、营收增长率、换手率、
#市盈率(PE)、市净率(PB)、市销率(PS)、总资产收益率因子
#还是先导入jqdata和技术分析工具
import jqdata
from jqlib.technical_analysis import *
#同样选择沪深300成分股做股票池
stocks = get_index_stocks('000300.XSHG')
q = query(valuation.code, valuation.market_cap,
balance.total_current_assets- balance.total_current_liability,
balance.total_liability- balance.total_assets,
balance.total_liability/balance.equities_parent_company_owners,
(balance.total_assets-balance.total_current_assets)/balance.total_assets,
balance.equities_parent_company_owners/balance.total_assets,
indicator.inc_total_revenue_year_on_year,
valuation.turnover_ratio,
valuation.pe_ratio,
valuation.pb_ratio,
valuation.ps_ratio,indicator.roa).filter(
valuation.code.in_(stocks))
#将获得的因子值存入一个数据表
df = get_fundamentals(q, date = None)
#把数据表的字段名指定为对应的因子名
df.columns = ['code', '市值', '净营运资本',
'净债务', '产权比率','非流动资产比率',
'股东权益比率', '营收增长率'
,'换手率','PE','PB','PS','总资产收益率']
#检查结果
df.head()
需要在聚宽的环境才能获得上面的数据,本地Python是出不来的。
设置一下股票代码作为索引,获取一些时间格式。
#将股票代码作为数据表的index
df.index = df.code.values
#使用del也可以删除列
del df['code']
#下面来把时间变量都定义好
today = datetime.datetime.today()
#设定3个时间差,分别是50天,1天和2天
delta50 = datetime.timedelta(days=50)
delta1 = datetime.timedelta(days=1)
delta2 = datetime.timedelta(days=2)
#50日前作为一个历史节点
history = today - delta50
#再计算昨天和2天前的日期
yesterday = today - delta1
two_days_ago = today - delta2
再然后获取一些技术指标数据:
#下面就获取股票的动量线、成交量、累计能量线、平均差、
#指数移动平均、移动平均、乖离率等因子
#时间范围都设为10天
df['动量线']=list(MTM(df.index, two_days_ago, timeperiod=10, unit = '1d',
include_now = True, fq_ref_date = None).values())
df['成交量']=list(VOL(df.index, two_days_ago, M1=10 ,unit = '1d', include_now = True,
fq_ref_date = None)[0].values())
df['累计能量线']=list(OBV(df.index,check_date=two_days_ago, timeperiod=10).values())
df['平均差']=list(DMA(df.index, two_days_ago, N1 = 10, unit = '1d', include_now = True,
fq_ref_date = None)[0].values())
df['指数移动平均']=list(EMA(df.index, two_days_ago, timeperiod=10, unit = '1d', include_now = True,
fq_ref_date = None).values())
df['移动平均']=list(MA(df.index, two_days_ago, timeperiod=10, unit = '1d', include_now = True,
fq_ref_date = None).values())
df['乖离率']=list(BIAS(df.index,two_days_ago, N1=10, unit = '1d', include_now = True,
fq_ref_date = None)[0].values())
#把数据表中的空值用0来代替
df.fillna(0,inplace=True)
#检查是否成功
df.head()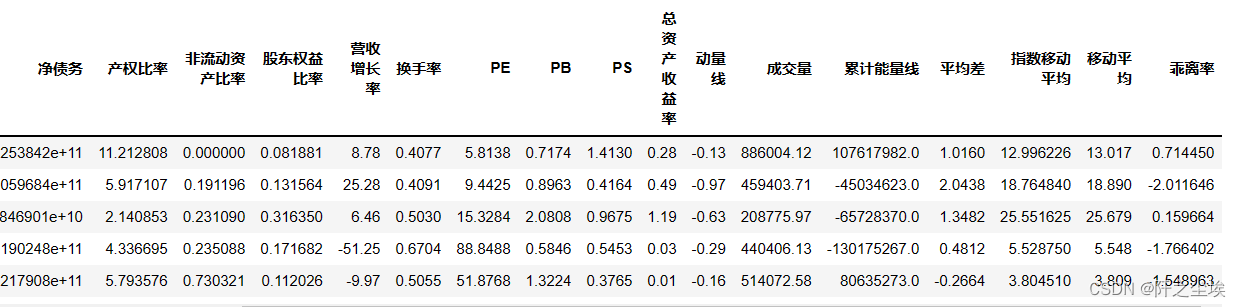
这样就获得了很多X,即特征变量,即因子。
下面构建y,我们的响应变量是一个分类的变量,即是否获得了超过市场的平均回报的收益率,是的话为1,不是为0 。
这里使用前一日的收盘价除以前50天的收盘价 然后减去1,作为收益率的值,计算出那些收益率大于均值的样本股则y为1 ,否则为0 。
#获取股票前一日的收盘价
df['close1']=list(get_price(stocks, end_date=yesterday,
count = 1,fq='pre',panel=False)['close'])
#获取股票50日前的收盘价
df['close2']=list(get_price(stocks, end_date=history,
count = 1,fq ='pre',panel=False)['close'])
#计算出收益
df['return']=df['close1']/df['close2']-1
#如果收益大于平均水平,则标记为1
#否则标记为0
df['signal']=np.where(df['return']<df['return'].mean(),0,1)
#检查是否成功
df.head()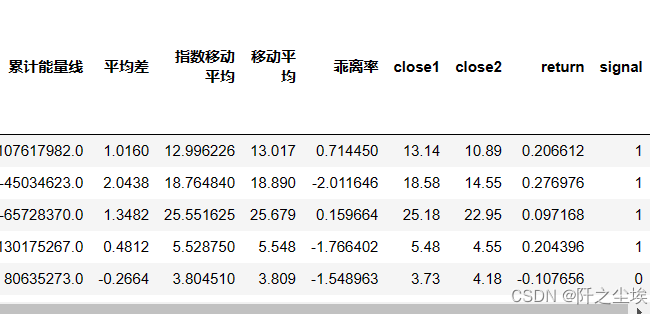
可以看到最后一列是我们的响应变量y。
模型构建
将X和y都准备好。划分训练集和测试集,导入随机森林分类器。
#导入数据集拆分工具
from sklearn.model_selection import train_test_split
#导入随机森林分类器
from sklearn.ensemble import RandomForestClassifier
#把因子值作为样本的特征,所以要去掉刚刚添加的几个字段
X = df.drop(['close1', 'close2', 'return', 'signal'], axis = 1)
#把signal作为分类标签
y = df['signal']
#将数据拆分为训练集和验证集
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size = 0.2)
#创建随机森林分类器实例,指定random_state便于复现
clf = RandomForestClassifier(n_estimators=5000,random_state=100)
#拟合训练集数据
clf.fit(X_train, y_train)
#查看分类器在训练集和验证集中的准确率
print(clf.score(X_train, y_train),
clf.score(X_test, y_test))![]()
分类问题,所以采用随机森林分类器,然后进行拟合和评价。
可以看到在训练集上的准确率为100%,在测试集删高的准确率为0.9333,说明模型的拟合效果很不错。
因子重要性
接下来使用随机森林的变量的重要性排序,原理是基础学习器决策树分裂时,若一个变量分裂时让损失函数下降得越多,说明这个变量越重要。
#为了便于观察,我们创建一个数据表
#数据表有两个字段,分别是特征名和重要性
#特征名就是因子的名称
factor_weight = pd.DataFrame({'features':list(X.columns),
'importance':clf.feature_importances_}).sort_values(
#这里根据重要程度降序排列,一遍遍找到重要性最高的特征
by='importance', ascending = False)
#检查结果
factor_weight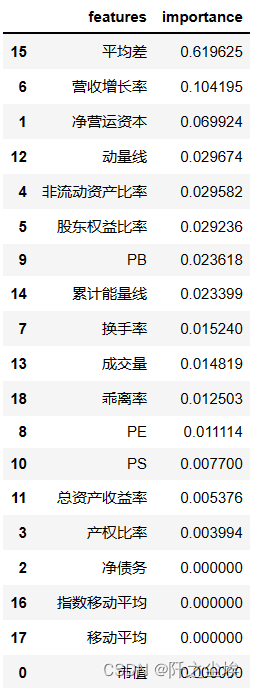
可以看到最重要的变量是技术指标平均差。这也是肯定的,因为平均差里面包含了过去和现在的股价信息最多,和我们的响应变量最为相似。
画图更加直观的查看变量重要性排序。
import seaborn as sns
plt.figure(figsize=(6,4),dpi=128)
sns.barplot(y=factor_weight['features'],x=factor_weight['importance'],orient="h")
plt.xlabel('重要程度')
plt.ylabel('因子名称')
plt.xticks(fontsize=10,rotation=35)
plt.title("因子重要性对比")
plt.show()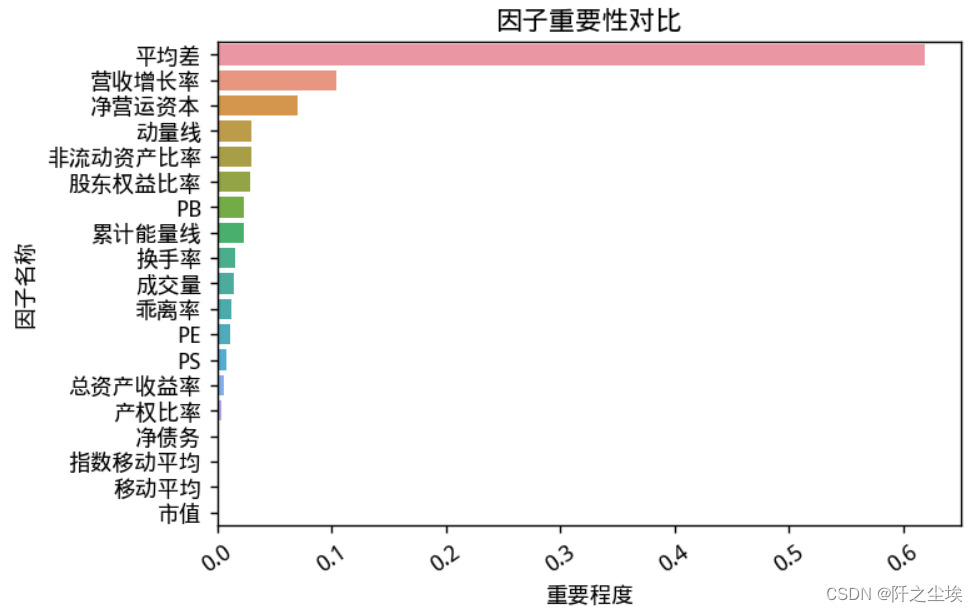
和上面结论一样,技术指标平均差对我们的响应变量是否获得超额回报的影响最大,然后是公司本身的财务指标,营业收入增长率,净收运营资本等。
选股策略
接下来我们使用对于表格数据最强的机器学习方法,轻量梯度提升方法——LGBM模型,对我们的股票市值进行预测,然后选取实际值和预测值差距最大的股票作为选股策略。即选取价值被低估的股票。
此时y是股票市值,X是前面那些财务技术指标
X=df.iloc[:,1:-3]
y=df.iloc[:,0]构建回归器
from lightgbm import LGBMRegressor
model = LGBMRegressor(n_estimators=100,objective='regression', random_state=0)
model.fit(X, y)
model.score(X, y)![]()
整体模型的拟合优度为86%,还不错。
用真实值减去预测值,然后进行排序,算的找出前10 的被低估的公司
diff = pd.DataFrame(np.array(y)-model.predict(X), index = y.index, columns = ['预测值和真实值的差值'])
#将该数据表中的值,按生序进行排列
diff = diff.sort_values(by = '预测值和真实值的差值', ascending = True)
#找到市值被低估最多的10只股票
diff.head(10)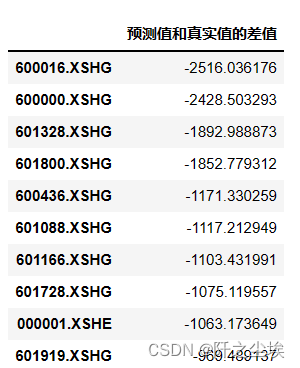
前十都是被低估了,负得越多说明被低估的越厉害。
受限于框架的使用,该策略我本人没有进行回测检验其收益率。书上的收益率大概是年化6%,不高,但是也算不错了。
(本案例仅作为策略研究,不构成任何投资意见。)