题目链接 :leetcode第 N 个泰波那契数
目录
题目解析:
算法原理
1.状态表示
2.状态转移方程
3.初始化
4.填表顺序
5.返回值
编写代码
题目解析:

题目让我们求第n个数的泰波那契数。
由题可得:

我们可以把它改写为:
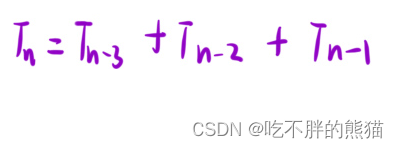
接着我们举几个例子,带入上面的公式来分析:
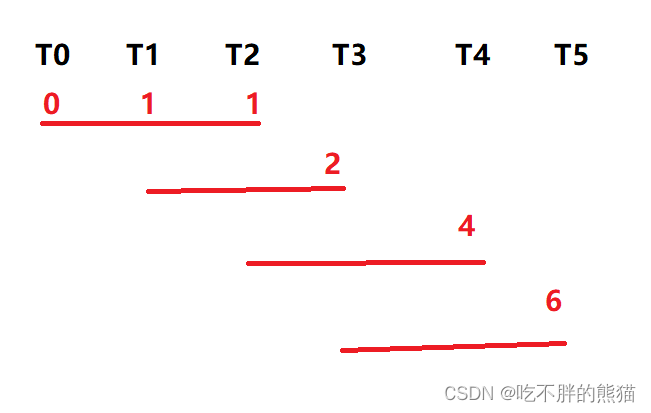
我们可以得到,当我们想得到当前位置的值就需要将前三个位置的值相加就可以得到;
算法原理:
1.状态表示
先创建一个dp表
首先先思考dp表里面的值所表示的含义(是什么?)
由上面的分析我们可以知道,我们可以用dp[i]来表示在第i处的泰波那契数为dp[i];
这种状态表示怎么来的?
1.题目要求
题目要求算出在n处的泰波那契数,所以算出dp[n]就可得出结果;
2.状态转移方程
dp[i]等于什么?
由上面的分析:
得dp[i]=dp[i-1]+dp[i-2]+dp[i-3];
3.初始化
(保证填表的时候不越界)
从上面的dp[i]公式,我们发现当i=0、1、2时等号后面的dp[i-1]、dp[i-2]、dp[i-3]会越界
所以我们这里需要将i=0、1、2初始化,并在写代码时在前面先条件判断;
4.填表顺序
(为了填写当前状态的时候,所需要的状态已经计算过了)
这里所需要的状态是:dp[i-1]、dp[i-2]、dp[i-3];
这几个数都是在i之前的,
所以我们这里是从左向右填表;
5.返回值
(根据题目要求和状态表示)
综上分析:
返回为:dp[n]
编写代码:

class Solution {
public:
int tribonacci(int n) {
//1.创建dp表
//2.初始化
//3.填表
//4.返回结果
if(n==0)
{
return 0;
}
else if(n==1||n==2)
{
return 1;
}
vector<int> dp(n+1);
dp[0]=0;
dp[1]=dp[2]=1;
for(int i=3;i<n+1;i++)
{
dp[i]=dp[i-3]+dp[i-2]+dp[i-1];
}
return dp[n];
}
};