1 微分方程的基本概念

1.1 微分方程

含导数或微分的方程,称为微分方程

1.2 微分方程的阶

微分方程中所含的导数或微分的最高阶数,称为该微分方程的阶数

1.3 微分方程的解

使得微分方程成立的函数,称为微分方程的解,微分方程的解可分为通解和特解

不含任意常数的微分方程的解,称为特解

含相互独立的任意常数的个数与微分方程阶数一致的微分方程的解,称为通解

2 一阶微分方程的种类及其解法

2.1 可分离变量的微分方程

2.1.1 定义

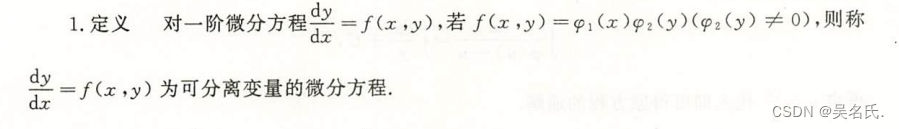
2.1.2 解法

2.1.3 例题

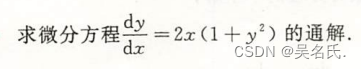
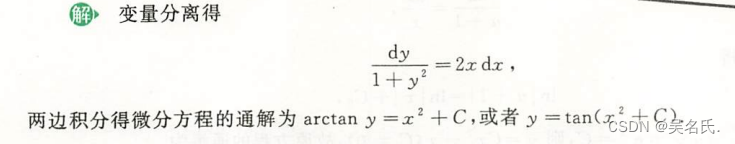
2.2 齐次微分方程

2.2.1 定义

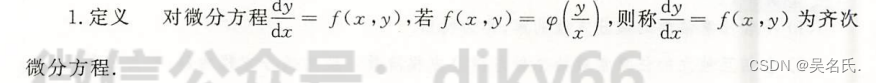
2.2.2 解法

2.2.3 例题

2.3 一阶齐次线性微分方程

2.3.1 定义

2.3.2 解法

2.3.3 例题

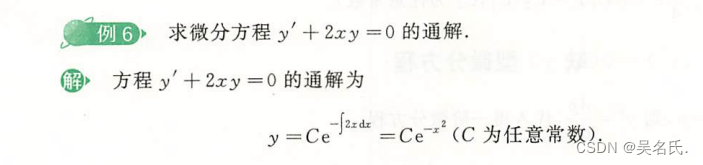
2.4 一阶非齐次线性微分方程

2.4.1 定义

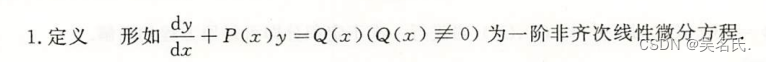
2.4.2 解法

3 可降解的高阶微分方程

3.1 y的n阶 = f(x) (n>=2)型微分方程

3.1.1 解法

3.1.2 例题

3.2 f(x,y’,y’') = 0(缺y)型微分方程

3.2.1 解法

3.2.2 例题

3.3 f(y,y’,y’') = 0(缺y)型微分方程

3.3.1 解法

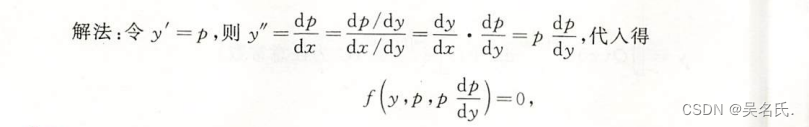
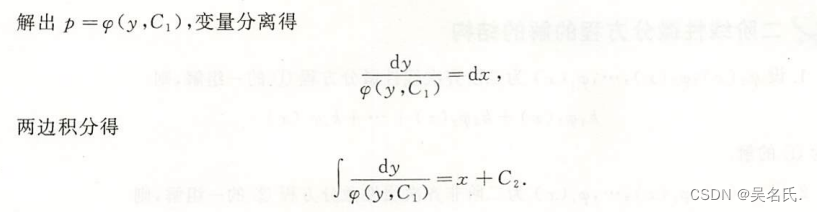
3.3.2 例题

4 高阶线性微分方程

4.1 基本概念

4.1.1 二阶齐次线性微分方程

4.1.2 二阶非齐次线性微分方程

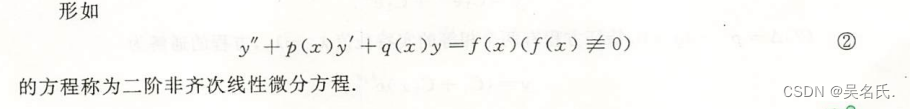
4.2 二阶常系数线性微分方程的解

4.2.1 二阶常系数齐次线性微分方程

4.2.2 二阶常系数非齐次线性微分方程