常见的类 nn.Conv2d，nn.BatchNorm2D，nn.AdaptiveAvgPool2d

nn.Conv2d
- 理论部分
- 代码部分
- - PaddlePaddle 版
  - torch 版
  - 分析
nn.BatchNorm2D
- 理论部分
- 代码部分
- - PaddlePaddle 版
  - Torch 版
  - 分析
  - - PaddlePaddle 版
    - Torch 版
nn.AdaptiveAvgPool2d
- 理论部分
- 代码部分
- - PaddlePaddle 版
  - 分析
  - Torch 版

可以到适配的飞桨公开项目更好的理解：练习 PyTorch 中的常用类

项目随文更。

nn.Conv2d

理论部分

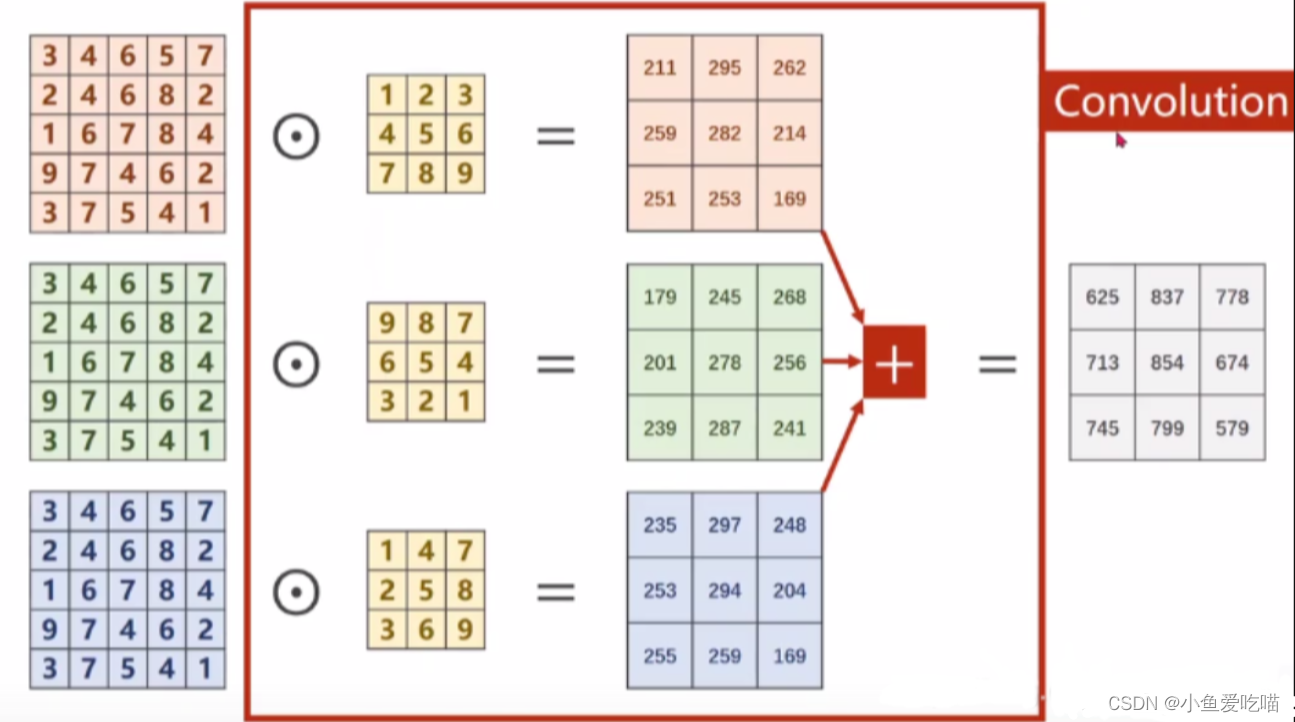
nn.Conv2d 是 PyTorch 中的一个二维卷积层（Convolutional Layer）类，用于处理二维图像数据或者序列信号数据（比如语音、文本等）。它可以实现二维卷积操作，通过卷积核对输入特征图进行滑动，提取出不同位置的特征信息，得到一个新的特征图。

在使用 nn.Conv2d 时，需要指定卷积核的一些参数，包括输入通道数、输出通道数、卷积核大小、步长、填充方式、偏差项等。具体来说，参数说明如下：

in_channels：输入的通道数，即特征图的深度（depth）。
out_channels：输出的通道数，即卷积核的个数。每个卷积核可以提取一种特征，并得到一张新的特征图。
kernel_size：卷积核的大小，是一个数值或者一个元组，比如 3 或者 (3, 3)。这里的大小表示卷积核的高和宽。
stride：步长，表示卷积核在输入特征图上滑动的步长。也是一个数值或者一个元组，比如 1 或者 (2, 2)。
padding：填充方式，指在输入特征图的边缘添加一些像素，这样可以使得输出特征图的大小和输入特征图的大小相同。padding 可以是一个数值或则一个元组，表示在每个维度上的填充量。比如 padding=1 表示在每个边缘添加一行或一列像素。
dilation：空洞卷积（Dilated Convolution）操作，也称为扩张卷积，可以增加卷积核之间的距离，从而使得感受野更加广阔。这里为默认值 1。
groups：分组卷积（Grouped Convolution）操作，能够将卷积核划分成多个组，每个组内部只对输入的一部分通道进行卷积操作。这里为默认值 1。
bias：偏差项（Bias Term），默认为 True，表示是否添加偏差项。

nn.Conv2d 的输入是一个四维张量，其形状为 (batch_size, in_channels, height, width)，其中 batch_size 表示样本的数量，in_channels 表示输入特征图的通道数，height 和 width 分别表示输入特征图的高度和宽度。

输出也是一个四维张量，其形状为 (batch_size, out_channels, height’, width’)，其中 height’ 和 width’ 表示卷积后得到的新的特征图的高度和宽度。

整个卷积层的尺寸为（m * n * k1 * k2）是一个4维张量，其中 m 表示卷积核的数量，n 表示通道数量，k1 表示每一个卷积核通道的宽，k2 表示每一个卷积核通道的高。

代码部分

nn.Conv2d(in_channels，out_channels，kernel_size，stride=1，padding=0，dilation=1，groups=1，bias=True)

PaddlePaddle 版

import paddle
import paddle.nn as nn
import paddle.nn.functional as F
 
in_channels = 5  #输入通道数量
out_channels =10 #输出通道数量
width = 100      #每个输入通道上的卷积尺寸的宽
height = 100     #每个输入通道上的卷积尺寸的高
kernel_size = 3  #每个输入通道上的卷积尺寸
batch_size = 1   #批数量
 
input = paddle.randn([batch_size, in_channels, width, height])
conv_layer = nn.Conv2D(in_channels=in_channels,
                      out_channels=out_channels,
                      kernel_size=kernel_size,
                      stride=1)
 
out_put = conv_layer(input)
 
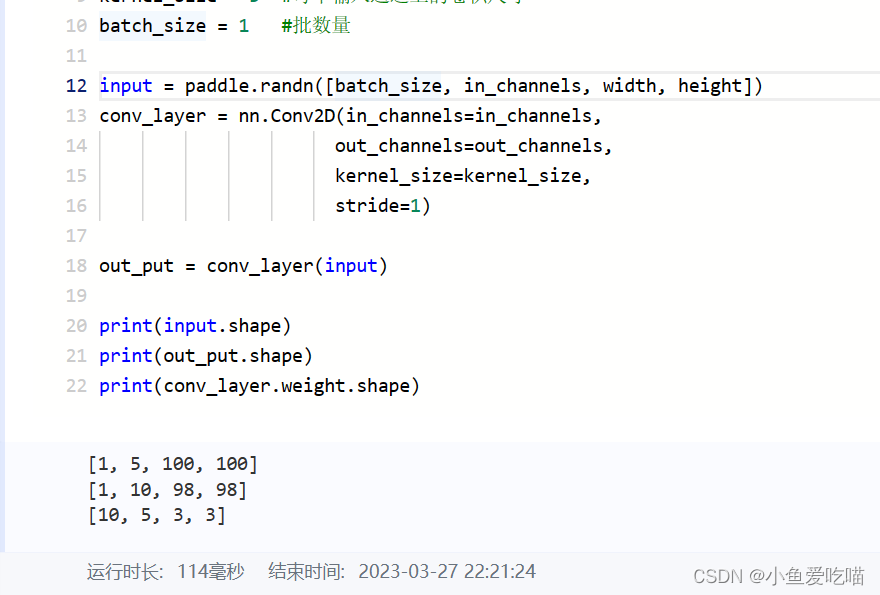
print(input.shape)
print(out_put.shape)
print(conv_layer.weight.shape)

输出如下：
在这里插入图片描述

torch 版

import torch
 
in_channels = 5  #输入通道数量
out_channels =10 #输出通道数量
width = 100      #每个输入通道上的卷积尺寸的宽
heigth = 100     #每个输入通道上的卷积尺寸的高
kernel_size = 3  #每个输入通道上的卷积尺寸
batch_size = 1   #批数量
 
input = torch.randn(batch_size,in_channels,width,heigth)
conv_layer = torch.nn.Conv2d(in_channels,out_channels,kernel_size=kernel_size)
 
out_put = conv_layer(input)
 
print(input.shape)
print(out_put.shape)
print(conv_layer.weight.shape)

输出如下：

在这里插入图片描述

分析

输入的张量信息为 [1,5,100,100] 分别表示 batch_size，in_channels，width，height；
输出的张量信息为 [1,10,100,100] 分别表示 batch_size，out_channels，width’，height’，其中 width’，height’ 表示卷积后的每个通道的新尺寸大小；
conv_layer.weight.shape 的输出结果为 [10, 5, 3, 3]，分表表示 out_channels，in_channels，kernel_size ，kernel_size ，可以看到与上面的公式 m * n * k1 * k2 一致。

nn.BatchNorm2D

nn.BatchNorm2D 是 PaddlePaddle 库中用于实现二维批量归一化（Batch Normalization）操作的类。

理论部分

在深度神经网络训练过程中，网络参数的更新通常会伴随着数据分布的变化，这会造成后续层的输入分布不稳定，从而导致训练难以收敛。批量归一化通过对每个小批次数据分别进行规范化，将数据分布调整到均值为0、方差为1的标准正态分布，从而增强了网络的泛化能力，加快了训练速度，同时还有一定的正则化效果。

nn.BatchNorm2D 通过对每个特征通道（feature map）上的数据进行均值和方差的归一化操作，增强了网络的表征能力，使得网络的输出更加稳定，提高了模型的准确性。具体来说，它可以在数据预处理、网络训练和网络推断三个阶段都进行归一化处理，使得训练过程更加稳定，提高了模型的鲁棒性。

nn.BatchNorm2D 的参数如下：

num_features：一般输入数据为 batch_size * num_features * height *
width，即为其中 num_features 特征维度数；
eps：分母添加到方差估计中的小量，避免分母为0，默认为：1e-5；
momentum (float) ：动量参数，一个用于运行过程中均值和方差的一个估计参数；

在训练时，每次计算完一批(batch)数据的卷积或全连接结果后，我们需要将该批数据的输出特征图沿着 batch_size 这一维进行统计。具体地，

我们计算该批数据中每个通道上的均值和方差，并将其保存下来。
然后，我们使用这些均值和方差对该批数据的输出特征图进行标准化处理，得到标准化的输出特征图。

为了进一步提高归一化的效果，我们通常还会在标准化之后，再引入可学习的偏移(offset)和缩放(scale)参数，以便让网络能够自适应地学习到更好的表示。具体地，

对于每个特征通道，我们引入两个可学习的参数gamma和beta，将标准化后的输出特征图进行缩放和平移，得到最终的输出特征图。

BatchNorm2d()函数数学原理如下：

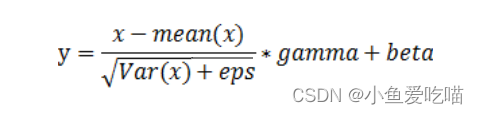
在这里插入图片描述

代码部分

PaddlePaddle 版

import paddle
import paddle.nn as nn

#eps:default:1e-5 (公式中为数值稳定性加到分母上的值)
m=nn.BatchNorm2D(2) #与PyTorch不同，PaddlePaddle中的BatchNorm层默认情况下是开启可学习参数的，
                    #无需设置weight和bias参数来启用可学习参数
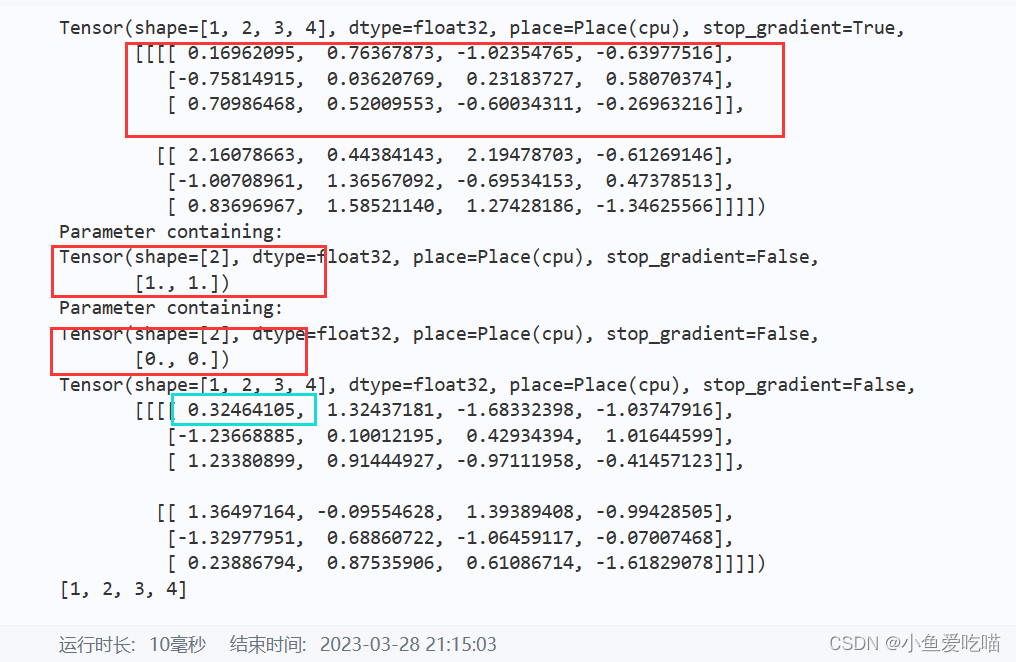
input=paddle.randn([1,2,3,4])
output=m(input)
 
print(input)
print(m.weight)
print(m.bias)
print(output)
print(output.shape)

输出如下：
在这里插入图片描述

Torch 版

#encoding:utf-8
import torch
import torch.nn as nn
#num_features - num_features from an expected input of size:batch_size*num_features*height*width
#eps:default:1e-5 (公式中为数值稳定性加到分母上的值)
#momentum:动量参数，用于running_mean and running_var计算的值，default：0.1
m=nn.BatchNorm2d(2,affine=True) #affine参数设为True表示weight和bias将被使用
input=torch.randn(1,2,3,4)
output=m(input)
 
print(input)
print(m.weight)
print(m.bias)
print(output)
print(output.size())

输出如下：

tensor([[[[ 1.4174, -1.9512, -0.4910, -0.5675],
          [ 1.2095,  1.0312,  0.8652, -0.1177],
          [-0.5964,  0.5000, -1.4704,  2.3610]],
 
         [[-0.8312, -0.8122, -0.3876,  0.1245],
          [ 0.5627, -0.1876, -1.6413, -1.8722],
          [-0.0636,  0.7284,  2.1816,  0.4933]]]])
Parameter containing:
tensor([0.2837, 0.1493], requires_grad=True)
Parameter containing:
tensor([0., 0.], requires_grad=True)
tensor([[[[ 0.2892, -0.4996, -0.1577, -0.1756],
          [ 0.2405,  0.1987,  0.1599, -0.0703],
          [-0.1824,  0.0743, -0.3871,  0.5101]],
 
         [[-0.0975, -0.0948, -0.0347,  0.0377],
          [ 0.0997, -0.0064, -0.2121, -0.2448],
          [ 0.0111,  0.1232,  0.3287,  0.0899]]]],
       grad_fn=<NativeBatchNormBackward>)
torch.Size([1, 2, 3, 4])

分析

PaddlePaddle 版

输入是一个1 * 2 * 3 * 4 四维矩阵，gamma 和 beta 为一维数组，是针对 input[0][0]，input[0][1] 两个3 * 4的二维矩阵分别进行处理的，我们不妨将 input[0][0] 的按照上面介绍的基本公式来运算，看是否能对的上 output[0][0] 中的数据。首先我们将 input[0][0] 中的数据输出，并计算其中的均值和方差。

print("输入的第一个维度:")
print(input[0][0]) #这个数据是第一个3*4的二维数据

#求第一个维度的均值和方差
# axis=0表示按照第一个维度(通道维度)进行求均值和方差
firstDimenMean=paddle.mean(input[0][0])
firstDimenVar=paddle.var(input[0][0], unbiased=False)  
# unbiased参数设置为False，表示使用无偏方差计算方式，贝塞尔校正不会被使用
print(m)
print(firstDimenMean)
print(firstDimenVar)

PaddlePaddle 输出如下：

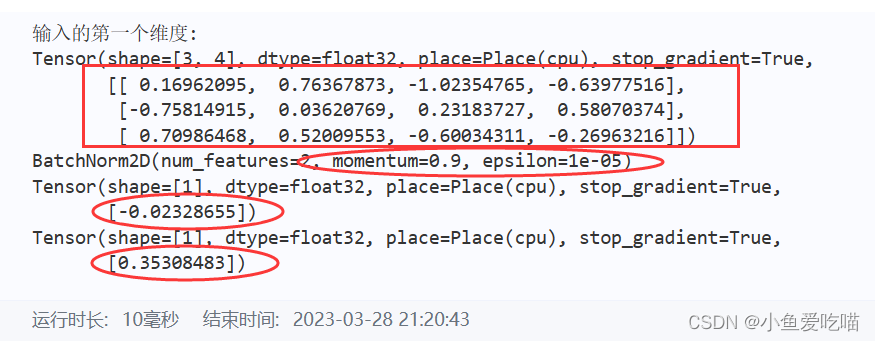
在这里插入图片描述

注意，这里 momentum 默认为0.9，epsilon 默认为1e-05。

我们可以通过计算器(线上Desmos计算器)计算出均值和方差均正确计算。以均值举例：

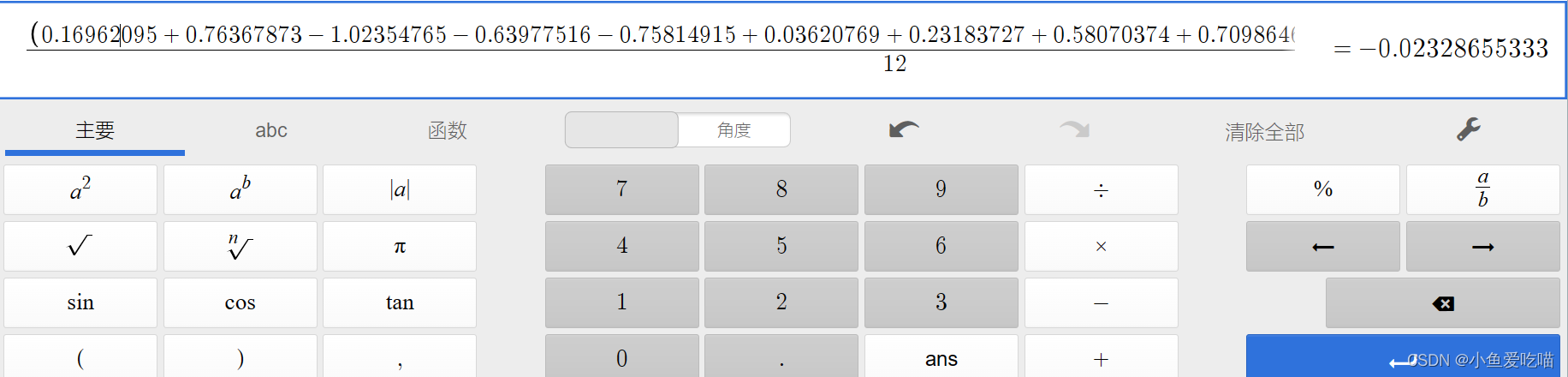
在这里插入图片描述

最后通过公式计算 input[0][0][0][0] 的值，代码如下：

batchnormone=((input[0][0][0][0]-firstDimenMean)/(paddle.sqrt(firstDimenVar+1e-5)))\
    *m.weight[0]+m.bias[0]
print(batchnormone)
print(m.weight[0])
print(m.bias[0])

输出的结果值等于 output[0][0][0][0]，代码和公式完美的对应起来了。
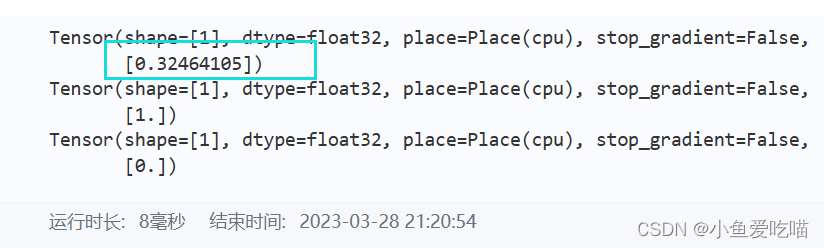
在这里插入图片描述

Torch 版

print("输入的第一个维度:")
print(input[0][0]) #这个数据是第一个3*4的二维数据
#求第一个维度的均值和方差
firstDimenMean=torch.Tensor.mean(input[0][0])
firstDimenVar=torch.Tensor.var(input[0][0],False)   #false表示贝塞尔校正不会被使用
print(m)
print('m.eps=',m.eps)
print(firstDimenMean)
print(firstDimenVar)

输出结果如下：

输入的第一个维度:
tensor([[ 1.4174, -1.9512, -0.4910, -0.5675],
        [ 1.2095,  1.0312,  0.8652, -0.1177],
        [-0.5964,  0.5000, -1.4704,  2.3610]])
BatchNorm2d(2, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
m.eps= 1e-05
tensor(0.1825)
tensor(1.4675)

最后通过公式计算input[0][0][0][0]的值，代码如下：

batchnormone=((input[0][0][0][0]-firstDimenMean)/(torch.pow(firstDimenVar,0.5)+m.eps))\
    *m.weight[0]+m.bias[0]
print(batchnormone)

输出结果如下：

tensor(0.2892, grad_fn=<AddBackward0>)

结果值等于 output[0][0][0][0]。ok，代码和公式也完美的对应起来了。

nn.AdaptiveAvgPool2d

nn.AdaptiveAvgPool2d(output_size)

理论部分

PyTorch 中的 nn.AdaptiveAvgPool2d 模块，是一个自适应的平均池化层，可以根据输入的尺寸自动调整池化窗口的大小，将任意大小的输入数据进行池化，并输出指定大小的特征图。在实例化 nn.AdaptiveAvgPool2d 层时，需要指定 output_size 参数，该参数是一个二元组，用于表示输出的特征图的大小 (H, W)。

在对输入尺寸为（B, C, H_in, W_in）的数据进行前向传播时，nn.AdaptiveAvgPool2d 层会自动计算出池化窗口的大小（K_H,K_W），使得输入的每个通道上的特征图都被均匀地划分为 K_H * K_W 个小块，然后对每个小块内的特征值求平均，最终输出一个 (B, C, H, W) 大小的特征图。

自适应池化层与传统的池化层不同，传统池化层通常需要手动设置池化窗口的大小和步幅，而自适应池化层则可以根据输入数据的大小自动调整池化窗口的大小，从而灵活地适应各种输入尺寸的情况。

nn.AdaptiveAvgPool2d 层只适用于二维输入数据，如果输入数据是三维或更高维的，则需要使用其他的自适应平均池化层，如 nn.AdaptiveAvgPool3d。

代码部分

PaddlePaddle 版

import paddle
import paddle.nn as nn
m = nn.AdaptiveAvgPool2D((2,1))
m1 = nn.AdaptiveAvgPool2D((None,5))
m2 = nn.AdaptiveAvgPool2D(1)

input = paddle.randn([2, 4, 3, 4])
output = m(input)
output1 = m1(input)
output2 = m2(input)

print('nn.AdaptiveAvgPool2D((2,1)):',output.shape)
print('nn.AdaptiveAvgPool2D((None,5)):',output1.shape)
print('nn.AdaptiveAvgPool2D(1):',output2.shape)

输出如下：

在这里插入图片描述

可以具体打印出来看看里面的数：

print(input)
print(output)
print(output1)
print(output2)

输出如下，非常直观：

Tensor(shape=[2, 4, 3, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
       [[[[ 0.90092957,  1.49062014, -0.43891591,  2.49542785],
          [-1.15749526, -0.30942214,  0.72686249,  0.19894561],
          [-0.52102602,  0.51292664, -0.14769700, -0.27466503]],

         [[ 0.76802170,  1.88680339,  1.33473635, -0.10681593],
          [ 0.21126194, -0.55997390, -0.51836526, -0.60124677],
          [-0.55262327, -1.67555463, -0.39201534, -2.58948588]],

         [[-0.32876831, -0.29057825, -0.34900934, -0.31911403],
          [-0.24603273,  0.02774601,  0.63011044, -1.04943550],
          [ 0.03737868, -0.79992193,  0.00638078, -0.97455049]],

         [[-0.42034203,  0.96777660,  0.62801188, -0.88072026],
          [-0.51847357,  1.37803781,  1.34817588, -0.74566907],
          [ 0.02777599, -0.05300835,  0.62294286,  0.29386613]]],


        [[[ 1.39181197,  1.51279640,  1.32197428,  1.23052955],
          [ 0.15545924,  1.01186311,  1.25041449,  0.07155325],
          [ 0.67657405, -1.73660100, -0.21091940, -0.02831869]],

         [[ 0.34955356,  0.06948886, -0.62700498, -0.93837327],
          [-0.32064596, -0.33115095,  0.88660580, -0.39552480],
          [-1.19203579, -4.19258356, -1.44245422,  2.13827157]],

         [[ 0.12091599,  0.69894040, -0.85016263, -0.84999377],
          [-0.61187607, -0.47178757,  0.24921176,  0.20200004],
          [ 1.90948820,  1.44339752, -0.48322666,  0.58571112]],

         [[-0.80645448,  1.03674793,  1.61488795, -1.18364632],
          [-0.81818682, -0.20740594, -0.60765731, -1.58125830],
          [-0.15702702,  0.91145509,  0.97826558, -1.30869794]]]])
Tensor(shape=[2, 4, 2, 1], dtype=float32, place=Place(cpu), stop_gradient=True,
       [[[[ 0.48836899],
          [-0.12144634]],

         [[ 0.30180269],
          [-0.83475041]],

         [[-0.24063522],
          [-0.29604059]],

         [[ 0.21959963],
          [ 0.29420596]]],


        [[[ 0.99330032],
          [ 0.14875315]],

         [[-0.16338146],
          [-0.60618973]],

         [[-0.18909398],
          [ 0.35286474]],

         [[-0.31912166],
          [-0.34881410]]]])
Tensor(shape=[2, 4, 3, 5], dtype=float32, place=Place(cpu), stop_gradient=True,
       [[[[ 0.90092957,  1.19577479,  0.52585208,  1.02825594,  2.49542785],
          [-1.15749526, -0.73345870,  0.20872018,  0.46290404,  0.19894561],
          [-0.52102602, -0.00404969,  0.18261482, -0.21118101, -0.27466503]],

         [[ 0.76802170,  1.32741261,  1.61076987,  0.61396021, -0.10681593],
          [ 0.21126194, -0.17435598, -0.53916955, -0.55980599, -0.60124677],
          [-0.55262327, -1.11408901, -1.03378499, -1.49075055, -2.58948588]],

         [[-0.32876831, -0.30967328, -0.31979379, -0.33406168, -0.31911403],
          [-0.24603273, -0.10914336,  0.32892823, -0.20966253, -1.04943550],
          [ 0.03737868, -0.38127163, -0.39677057, -0.48408484, -0.97455049]],

         [[-0.42034203,  0.27371728,  0.79789424, -0.12635419, -0.88072026],
          [-0.51847357,  0.42978212,  1.36310685,  0.30125341, -0.74566907],
          [ 0.02777599, -0.01261618,  0.28496724,  0.45840448,  0.29386613]]],


        [[[ 1.39181197,  1.45230412,  1.41738534,  1.27625191,  1.23052955],
          [ 0.15545924,  0.58366120,  1.13113880,  0.66098386,  0.07155325],
          [ 0.67657405, -0.53001344, -0.97376019, -0.11961904, -0.02831869]],

         [[ 0.34955356,  0.20952120, -0.27875805, -0.78268909, -0.93837327],
          [-0.32064596, -0.32589847,  0.27772743,  0.24554050, -0.39552480],
          [-1.19203579, -2.69230962, -2.81751895,  0.34790868,  2.13827157]],

         [[ 0.12091599,  0.40992820, -0.07561111, -0.85007823, -0.84999377],
          [-0.61187607, -0.54183185, -0.11128791,  0.22560591,  0.20200004],
          [ 1.90948820,  1.67644286,  0.48008543,  0.05124223,  0.58571112]],

         [[-0.80645448,  0.11514673,  1.32581794,  0.21562082, -1.18364632],
          [-0.81818682, -0.51279640, -0.40753162, -1.09445786, -1.58125830],
          [-0.15702702,  0.37721404,  0.94486034, -0.16521618, -1.30869794]]]])
Tensor(shape=[2, 4, 1, 1], dtype=float32, place=Place(cpu), stop_gradient=True,
       [[[[ 0.28970751]],

         [[-0.23293813]],

         [[-0.30464956]],

         [[ 0.22069782]]],


        [[[ 0.55392808]],

         [[-0.49965444]],

         [[ 0.16188486]],

         [[-0.17741479]]]])

分析

原来输入的大小是 [2, 4, 3, 4]，见上图输出的四维矩阵，后来经过 nn.AdaptiveAvgPool2D((2,1)) 操作后，output 变成了 [2, 4, 2, 1] 大小的四维矩阵。

Torch 版

import torch
import torch.nn as nn
m = nn.AdaptiveAvgPool2d((5,1))
m1 = nn.AdaptiveAvgPool2d((None,5))
m2 = nn.AdaptiveAvgPool2d(1)
input = torch.randn(2, 64, 8, 9)
output = m(input)
output1 = m1(input)
output2 = m2(input)
print('nn.AdaptiveAvgPool2d((5,1)):',output.shape)
print('nn.AdaptiveAvgPool2d((None,5)):',output1.shape)
print('nn.AdaptiveAvgPool2d(1):',output2.shape)