数据结构初阶：链式二叉树的遍历解析及一些基本操作

news2024/10/5 15:24:39

目录

前置说明

一、 二叉树的遍历（理论）

        1. 二叉树的拆解

        2. 二叉树的前序（先根）遍历

        3. 二叉树的中序（中根）遍历

        4. 二叉树的后序（后根）遍历

        5. 二叉树的层序遍历

二、 代码实操

        1. 前序（先根）遍历代码实现

        2. 中序（中根）遍历代码实现

        3. 后序（后根）遍历代码实现 

        4. 求二叉树节点个数

        5. 求二叉树叶子节点个数

        6. 求二叉树高度

        7. 求第k层节点的个数（k>=1）

        8. 在二叉树中查找数据为x的节点

三、 测试代码

四、 全部代码

本期博客会详细阐述链式二叉树的一些操作

前置说明

这里由于普通链式二叉树是无规律的，所以对其进行增删查改是无意义的。

在这里并不会对链式二叉树进行增删查改的操作

后面我们还会陆续介绍搜索二叉树、平衡二叉树等等，这些二叉树的增删查改才是有意义的。

一、 二叉树的遍历（理论）

        1. 二叉树的拆解

在真正遍历二叉树数之前，我们先要有会拆解二叉树的思想，即把一棵二叉树拆分为多个根和子树。

下面看到这课二叉树：

我们来从上置下从左到右的顺序来拆解这课二叉树

第一次拆解：

先看到总体的二叉树可以被拆分为根为：  

左子树为：

右子树为：

第二次拆解：

我们先拿到第一次拆解的左子树发现其还可以拆解

被拆解后根为：

左子树为：

右子树为：NULL（空树不再进行拆解）

第三次拆解：

我们先拿到第二次拆解的左子树发现其还可以拆解

被拆解后根为：

左子树为：NULL（空树不再进行拆解）

右子树为：NULL（空树不再进行拆解）

第四次拆解：

总体二叉树的左子树已经被全部拆解完毕，接着对第一次拆解的右子树进行拆解

被拆解后根为：

左子树为：

右子树为：

第五次拆解：

接着对第四次拆解的左子树进行拆解

被拆解后根为：

左子树为：NULL（空树不再进行拆解）

右子树为：NULL（空树不再进行拆解）

第六次拆解：

接着对第四次拆解的右子树进行拆解

被拆解后根为：

左子树为：NULL（空树不再进行拆解）

右子树为：NULL（空树不再进行拆解）

经过六次后整个二叉树已经被全部拆解完毕，这样的拆解思想可以称为分治，步步细化层层到位。

        2. 二叉树的前序（先根）遍历

二叉树的前序（先根）遍历顺序是先遍历根，再遍历左子树，最后再遍历右子树，以此顺序遍历完整个二叉树。

还是拿这课二叉树来举例：

用前序（先根）遍历的方法遍历的过程为：先遍历整个二叉树的根：A

再遍历A节点的左子树：

该树的根节点为：B

接着遍历B节点的左子树：

该树的根节点为：D

然后再遍历D节点的左子树：NULL（不再向下遍历其根节点）

再遍历D节点的右子树：NULL（不再向下遍历其根节点）

现在B节点的左子树已经遍历完毕再遍历其右子树：NULL（不再向下遍历其根节点）

到这里整个二叉树的左子树已被遍历完毕，再遍历其右子树：

该树的根节点为：C

接着遍历C节点的左子树：

该树的根节点为：E

然后再遍历E节点的左子树：NULL（不再向下遍历其根节点）

再遍历E节点的右子树：NULL（不再向下遍历其根节点）

这里整个C节点的左子树已遍历完毕，再遍历其右子树：

该树的根节点为：F

然后再遍历F节点的左子树：NULL（不再向下遍历其根节点）

再遍历F节点的右子树：NULL（不再向下遍历其根节点）

最终整个二叉树的右子树也被遍历完成，前序（先根）遍历完成。

总顺序为：A->B->D->NULL->NULL->NULL->C->E->NULL->NULL->F->NULL->NULL

        3. 二叉树的中序（中根）遍历

二叉树的中序（中根）遍历顺序是先遍左子树，再遍历根，最后再遍历右子树，以此顺序遍历完整个二叉树。

再是拿这课二叉树来举例：

用中序（中根）遍历的方法遍历的过程为：先遍历整个二叉树的左子树：

再遍历以B为根节点的左子树：

接着遍历以D为根节点的左子树：NULL（不再向下遍历其左子树）

以D为根节点的左子树遍历完了，接着遍历其根：D

以D为根节点的树的根遍历完了，接着遍历其右子树：NULL（不再向下遍历其左子树）

以B为根节点的左子树遍历完了，接着遍历其根：B

以B为根节点的树的根遍历完了，接着遍历其右子树：NULL（不再向下遍历其左子树）

整个二叉树的左子树遍历完了，接着遍历其根：A

整个二叉树的根遍历完了，接着遍历其右子树：

再遍历以C为根节点的左子树：

接着遍历以E为根节点的左子树：NULL（不再向下遍历其左子树）

以E为根节点的左子树遍历完了，接着遍历其根：E

以E为根节点的树的根遍历完了，接着遍历其右子树：NULL（不再向下遍历其左子树）

以C为根节点的左子树遍历完了，接着遍历其根：C

以C为根节点的树的根遍历完了，接着遍历其右子树：

接着遍历以F为根节点的左子树：NULL（不再向下遍历其左子树）

以F为根节点的左子树遍历完了，接着遍历其根：F

以F为根节点的树的根遍历完了，接着遍历其右子树：NULL（不再向下遍历其左子树）

最终随着以C为根节点的右子树遍历完了，整个二叉树的右子树也被遍历完成，中序（中根）遍历完成。

总顺序为：NULL->D->NULL->B->NULL->A->NULL->E->NULL->C->NULL->F->NULL

        4. 二叉树的后序（后根）遍历

二叉树的后序（后根）遍历顺序是先遍左子树，再遍历右子树，最后再遍历根，以此顺序遍历完整个二叉树。

还是拿这课二叉树来举例：

用后序（后根）遍历的方法遍历的过程为：先遍历整个二叉树的左子树：

再遍历以B为根节点的左子树：

接着遍历以D为根节点的左子树：NULL（不再向下遍历其左子树）

以D为根节点的左子树遍历完了，接着遍历其右子树：NULL（不再向下遍历其左子树）

以D为根节点的右子树遍历完了，接着遍其根：D

以B为根节点的左子树遍历完了，接着遍历其右子树：NULL（不再向下遍历其左子树）

以B为根节点的右子树遍历完了，接着遍其根：B

整个二叉树的左子树遍历完了，接着遍历其右子树：

再遍历以C为根节点的左子树：

接着遍历以E为根节点的左子树：NULL（不再向下遍历其左子树）

以E为根节点的左子树遍历完了，接着遍历其右子树：NULL（不再向下遍历其左子树）

以E为根节点的右子树遍历完了，接着遍其根：E

以C为根节点的左子树遍历完了，接着遍历其右子树：

接着遍历以F为根节点的左子树：NULL（不再向下遍历其左子树）

以F为根节点的左子树遍历完了，接着遍历其右子树：NULL（不再向下遍历其左子树）

以F为根节点的右子树遍历完了，接着遍历其根：F

以C为根节点的右子树遍历完了，接着遍其根：C

整个二叉树的右子树也被遍历完成，接着遍其根：A

后序（后根）遍历完成。

总顺序为：NULL->NULL->D->NULL->B->NULL->NULL->E->NULL->NULL->F->C->A

        5. 二叉树的层序遍历

二叉树的层序遍历顺序是先左后右从上到下，一层一层遍历，以此顺序遍历完整个二叉树。

这个二叉树用层序遍历就是：A->B->C->D->E->F

二、 代码实操

下面我们来用代码来对二叉树进行一些基本操作

下面是对链式二叉树节点的代码结构：

typedef char DataType;
typedef struct BinaryTreeNode
{
	//数据
	DataType data;
	struct BinaryTreeNode* Left;//指向左孩子
	struct BinaryTreeNode* Right;//指向右孩子
}BTNode;

        1. 前序（先根）遍历代码实现

void PrevOrder(BTNode* root)//传入二叉树根节点
{
	if (root == NULL)//如果是空树就直接结束
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);//先遍历其根节点
	PrevOrder(root->Left);//递归遍历其左子树
	PrevOrder(root->Right);//递归遍历其右子树
}

        2. 中序（中根）遍历代码实现

void InOrder(BTNode* root)
{
	if (root == NULL)//如果是空树就直接结束
	{
		printf("NULL ");
		return;
	}
	InOrder(root->Left);//先递归遍历其左子树
	printf("%c ", root->data);//再遍历其根节点
	InOrder(root->Right);//最后递归遍历其右子树
}

        3. 后序（后根）遍历代码实现 

void PostOrder(BTNode* root)
{
	if (root == NULL)//如果是空树就直接结束
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->Left);//先递归遍历其左子树
	PostOrder(root->Right);//再递归遍历其右子树
	printf("%c ", root->data);//最后遍历其根节点
}

        4. 求二叉树节点个数

在求二叉树节点个数时，我们不能单一定义一个局部变量来实现，也不能定义一个静态变量来统计节点个数（静态变量除第一次再被函数调用时初始值是不一样的），在这里我们使用全局变量来实现：

int size = 0;
void CountTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	size++;
	CountTreeSize(root->Left);
	CountTreeSize(root->Right);
}
void TreeSize(BTNode* root)
{
	size = 0;//防止多次调用时初始值发生改变
	CountTreeSize(root);
}

但是还有一个更好的方法：

int TreeSize2(BTNode* root)
{
	return root == NULL ? 0 : TreeSize2(root->Left) + TreeSize2(root->Right) + 1;
}

这里我们层层递归统计最后将值合计返回（妙）！

        5. 求二叉树叶子节点个数

int TreeLeafSize(BTNode* root)
{
	if (root == NULL)//防止指针越界
		return 0;
	if (root->Left == NULL && root->Right == NULL)//是叶子节点就返回1
		return 1;
	return TreeLeafSize(root->Left) + TreeLeafSize(root->Right);//累加所有的返回值
}

        6. 求二叉树高度

int TreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	int LeftHeight = TreeHeight(root->Left);//记录左子树深度
	int RightHeight = TreeHeight(root->Right);//记录右子树深度
	return LeftHeight > RightHeight ? LeftHeight + 1 : RightHeight + 1;//返回较大子树的深度
}

        7. 求第k层节点的个数（k>=1）

int TreeKLevelSize(int k, BTNode* root)
{
	if (root == NULL)
		return 0;
	if (k == 1)//k=1是即是节点处于原本k层
		return 1;
	return TreeKLevelSize(k - 1, root->Left) + TreeKLevelSize(k - 1, root->Right);//每次递归到下一层k值减1
}

        8. 在二叉树中查找数据为x的节点

BTNode* TreeFind(BTNode* root,DataType x)
{
	if (root == NULL)
		return NULL;
	if (root->data == x)//找到返回其地址
		return root;
	BTNode* ret1 = TreeFind(root->Left, x);//在左子树中递归寻找
	if (ret1)//找到了返回其地址
		return ret1;
	BTNode* ret2 = TreeFind(root->Right, x);//在右子树中递归寻找
	if (ret2)//找到了返回其地址
		return ret2;
	return NULL;
}

三、 测试代码

BTNode* BuyBTNode(DataType x)//为二叉树节点申请空间
{
	BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
	if (newNode == NULL)
	{
		perror("malloc");
		exit(-1);
	}
	newNode->data = x;
	newNode->Left = NULL;
	newNode->Right = NULL;
}
void Test()
{
	BTNode* n1 = BuyBTNode('A');
	BTNode* n2 = BuyBTNode('B');
	BTNode* n3 = BuyBTNode('C');
	BTNode* n4 = BuyBTNode('D');
	BTNode* n5 = BuyBTNode('E');
	BTNode* n6 = BuyBTNode('F');
	BTNode* n7 = BuyBTNode('G');
	n1->Left = n2;
	n1->Right = n3;
	n2->Left = n4;
	n3->Left = n5;
	n3->Right = n6;
	n6->Left = n7;
	//上面都是手动构建二叉树
	PrevOrder(n1);
	printf("\n");
	InOrder(n1);
	printf("\n");
	PostOrder(n1);
	printf("\n");
	TreeSize(n1);
	printf("Tree Size:%d\n", size);
	TreeSize(n1);
	printf("Tree Size:%d\n", size);
	TreeSize(n1);
	printf("Tree Size:%d\n", TreeSize2(n1));
	printf("Tree Leaf Size:%d\n", TreeLeafSize(n1));
	printf("Tree Height:%d\n", TreeHeight(n1));
	printf("Tree 3 level Size:%d\n", TreeKLevelSize(3, n1));
	printf("The address of E is : %p", TreeFind(n1, 'E'));
}

下面是测试结果：

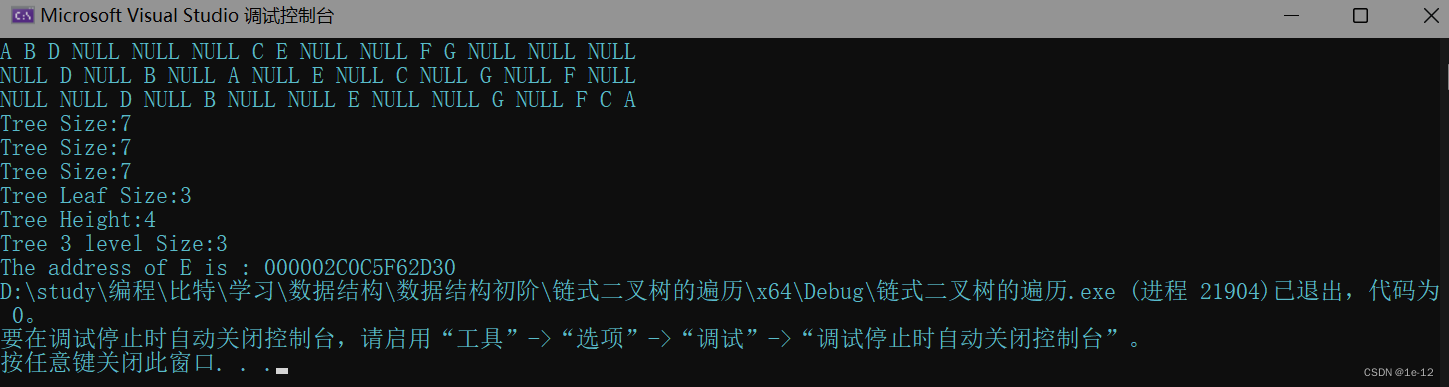
四、 全部代码

#include<stdio.h>
#include<stdlib.h>
typedef char DataType;
typedef struct BinaryTreeNode
{
	//数据
	DataType data;
	struct BinaryTreeNode* Left;//指向左孩子
	struct BinaryTreeNode* Right;//指向右孩子
}BTNode;


void PrevOrder(BTNode* root)//传入二叉树根节点
{
	if (root == NULL)//如果是空树就直接结束
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);//先遍历其根节点
	PrevOrder(root->Left);//递归遍历其左子树
	PrevOrder(root->Right);//递归遍历其右子树
}
void InOrder(BTNode* root)
{
	if (root == NULL)//如果是空树就直接结束
	{
		printf("NULL ");
		return;
	}
	InOrder(root->Left);//先递归遍历其左子树
	printf("%c ", root->data);//再遍历其根节点
	InOrder(root->Right);//最后递归遍历其右子树
}
void PostOrder(BTNode* root)
{
	if (root == NULL)//如果是空树就直接结束
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->Left);//先递归遍历其左子树
	PostOrder(root->Right);//再递归遍历其右子树
	printf("%c ", root->data);//最后遍历其根节点
}
int size = 0;
void CountTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	size++;
	CountTreeSize(root->Left);
	CountTreeSize(root->Right);
}
void TreeSize(BTNode* root)
{
	size = 0;//防止多次调用时初始值发生改变
	CountTreeSize(root);
}
int TreeSize2(BTNode* root)
{
	return root == NULL ? 0 : TreeSize2(root->Left) + TreeSize2(root->Right) + 1;
}
int TreeLeafSize(BTNode* root)
{
	if (root == NULL)//防止指针越界
		return 0;
	if (root->Left == NULL && root->Right == NULL)//是叶子节点就返回1
		return 1;
	return TreeLeafSize(root->Left) + TreeLeafSize(root->Right);//累加所有的返回值
}
int TreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	int LeftHeight = TreeHeight(root->Left);//记录左子树深度
	int RightHeight = TreeHeight(root->Right);//记录右子树深度
	return LeftHeight > RightHeight ? LeftHeight + 1 : RightHeight + 1;//返回较大子树的深度
}
int TreeKLevelSize(int k, BTNode* root)
{
	if (root == NULL)
		return 0;
	if (k == 1)//k=1是即是节点处于原本k层
		return 1;
	return TreeKLevelSize(k - 1, root->Left) + TreeKLevelSize(k - 1, root->Right);//每次递归到下一层k值减1
}
BTNode* TreeFind(BTNode* root,DataType x)
{
	if (root == NULL)
		return NULL;
	if (root->data == x)//找到返回其地址
		return root;
	BTNode* ret1 = TreeFind(root->Left, x);//在左子树中递归寻找
	if (ret1)//找到了返回其地址
		return ret1;
	BTNode* ret2 = TreeFind(root->Right, x);//在右子树中递归寻找
	if (ret2)//找到了返回其地址
		return ret2;
	return NULL;
}

本期博客到这里又要和大家说再见了，后面还会为各位看客带来二叉树更深入的讲解，请不要走开~

本期含递归代码较多，有较难理解的地方需要多画图慢慢消化，如有纰漏还请各位大佬不吝赐教呀

我们下期见！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/126994.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

PostFix+Dovecot 部署邮件系统

PostFix+Dovecot 部署邮件系统

Postfix 是一种电子邮件服务器是一个开放源代码的软件. Postfix 是MTA邮件传输代理软件.是sendmail提供替代品的一个尝试,在Internet世界中,大部分的电子邮件都是通过sendmail来投递的,大约有100万用户使用sendmail,每天投递上亿封邮件,Postfix试图更快、更容易管理、更安全,同…
阅读更多...
【bp靶场portswigger-服务端2】身份认证-16个实验（全）

【bp靶场portswigger-服务端2】身份认证-16个实验（全）

目录 一、身份验证定义 1、三个身份验证因素 2、身份验证和授权 3、身份验证漏洞的产生 4、实验的字典 二、基于密码的登录中的漏洞 1、强制策略 2、用户枚举 3、有缺陷的强力保护 实验1&#xff1a;通过不同响应的用户名枚举 实验4&#xff1a;通过细微不同的响应进…
阅读更多...
BPF学习笔记（六）-- 使用bpf实现xdp的例子

BPF学习笔记（六）-- 使用bpf实现xdp的例子

本篇文章参考《Linux Observability with BPF》中第7章的例子&#xff0c;主要功能是借助于ip命令作为前端&#xff0c;对其他主机访问tcp的8000端口进行限制&#xff0c;这里需要使用较新版本的iproute2软件工具包. 1. 下载编译iproute2 工具包&#xff0c;使用最新的ip命令…
阅读更多...
gRPC学习

gRPC学习

首先什么了解什么是RPC? 不同于 TCP 和 HTTP&#xff0c;TCP 和 HTTP 是网络传输协议&#xff0c;而 RPC 是一种设计、实现框架&#xff0c;通讯协议只是其中一部分&#xff0c;RPC 不仅要解决协议通讯的问题&#xff0c;还有序列化和反序列化&#xff0c;以及消息通知。 一…
阅读更多...
IDEA的使用技巧积累

IDEA的使用技巧积累

本文主要是记录一些在使用IDEA过程中遇到的一些问题解决方法、以及快捷键等 添加框架支持 打开模块设置 (文件—>项目结构也是同理) 主要用于配置模块&#xff0c;例如web&#xff0c;springboot模块 设置 主要设置maven的一些信息 CtrlShiftF (java代码审计基础中出现…
阅读更多...
WebSocket的基本使用

WebSocket的基本使用

目录 为何使用websocket 1.后端搭建 2.搭建webSocket前后分离 1.配置跨域过滤器与初始化websocket 2.定义websocket服务 3.定义控制器进行测试webSocket向前端发送消息 2.前端准备 3.进行测试 向后端发送消息测试 后端向前端发送消息测试 为何使用websocket 在浏览器…
阅读更多...
小型云台机械手红外搬运功能的实现

小型云台机械手红外搬运功能的实现

1. 功能说明 在小型云台机械手前方安装近红外传感器&#xff0c;如果近红外触发&#xff08;检测到有货物&#xff09;&#xff0c;机械手开始抓取货物&#xff0c;并将货物从一个区域搬运到另一个指定区域&#xff1b;否则&#xff0c;机械臂不动作。 2. 使用样机 本实验使用…
阅读更多...
【LeetCode】从前序与中序遍历序列构造二叉树 [M]（二叉树重构）

【LeetCode】从前序与中序遍历序列构造二叉树 [M]（二叉树重构）

105. 从前序与中序遍历序列构造二叉树 - 力扣&#xff08;LeetCode&#xff09; 一、题目 给定两个整数数组 preorder 和 inorder &#xff0c;其中 preorder 是二叉树的先序遍历&#xff0c; inorder 是同一棵树的中序遍历&#xff0c;请构造二叉树并返回其根节点。 示例 1&…
阅读更多...
ASEMI整流桥MB10S，DB207S和ABS210有什么区别

ASEMI整流桥MB10S，DB207S和ABS210有什么区别

编辑-Z ASEMI整流桥MB10S&#xff0c;DB207S和ABS210有什么区别&#xff1f;这几个型号从外观看都是很相似的&#xff0c;那么他们参数有什么不一样呢&#xff1f; MB10S参数&#xff1a; 型号&#xff1a;MB10S 封装&#xff1a;MBS-4 最大重复峰值反向电压&#xff08;VR…
阅读更多...
缓冲区Buffer类的设计（参考Muduo实现）

缓冲区Buffer类的设计（参考Muduo实现）

Buffer的功能需求&#xff1a; Buffer类的设计目的是再创造一层应用层缓冲区。 其对外表现为一块连续的内存(char* p, int len)&#xff0c;以方便客户代码的编写。 size() 可以自动增长&#xf…
阅读更多...
Java如何自定义一个变长数组？

Java如何自定义一个变长数组？

文章目录思路分析实现代码测试结果首先需要声明的是&#xff0c; Java本身是提供了变长数组的&#xff0c;即 ArrayList。那么自定义一个变长数组有啥用&#xff1f;其实没啥用或者说用处不大&#xff0c;主要就是为了了解下变长数组的设计理念而已。实际工作中直接使用 ArrayL…
阅读更多...
文华财经期货背离信号准确率高指标公式，单边趋势行情增仓上行多空共振策略

文华财经期货背离信号准确率高指标公式，单边趋势行情增仓上行多空共振策略

由“短线震荡波段王”和“三柱共振-高把握”指标合成 功能 : 1.红绿小波段黄蓝中波段粉青大波段 2.红绿中小波段 3.顶背底背提示 4.金叉死叉提示 5.多和空提示-金叉死叉改写 优点:宽幅震荡和窄幅震荡 弊端:单边行情(可结合多空趋势主图规避) 功能: 1.红绿波段 2.大中量仓-单…
阅读更多...
MySQL索引详解

MySQL索引详解

目录 1、为什么要有索引&#xff1f; 2、预备知识 3、为何IO交互要是 Page&#xff1f; 4、如何理解Page以及索引理解 5、索引操作 <1> 创建主键索引 <2> 创建唯一索引 <3> 普通索引的创建 <4> 全文索引的创建 <5> 查询索引 <5>…
阅读更多...
Python图像识别实战（五）：卷积神经网络CNN模型图像二分类预测结果评价（附源码和实现效果）

Python图像识别实战（五）：卷积神经网络CNN模型图像二分类预测结果评价（附源码和实现效果）

前面我介绍了可视化的一些方法以及机器学习在预测方面的应用&#xff0c;分为分类问题&#xff08;预测值是离散型&#xff09;和回归问题&#xff08;预测值是连续型&#xff09;&#xff08;具体见之前的文章&#xff09;。 从本期开始&#xff0c;我将做一个关于图像识别的…
阅读更多...
BOOT进程控制模式与故障排错

BOOT进程控制模式与故障排错

1. BOOT reboot and shutdown—使用systemctl 命令。 systemctl poweroff–关机 systemctl reboot --重启 systemctl halt 禁用CPU 在7版本中使用systemctl 工具。 选择systemd target graphical.target 桌面图形模式 multi-user.target 多用户模式–命令行 rescue.target 救援…
阅读更多...
Linux驱动开发基础__总线设备驱动模型

Linux驱动开发基础__总线设备驱动模型

目录 1 驱动编写的三种方法 1.1 传统写法 1.2 总线设备驱动模型 1.3 设备树 2 在 Linux 中实现“分离”&#xff1a;Bus/Dev/Drv 模型 3 匹配原则 4 函数调用关系 1 驱动编写的三种方法 1.1 传统写法 1.2 总线设备驱动模型 引入platform_device、platform_driver&…
阅读更多...
二叉数题型2

二叉数题型2

目录 二叉搜索树的众数 二叉树的最近公共祖先 修剪二叉树 二叉搜索树的众数 问题描述&#xff1a; 给你一个含重复值的二叉搜索树&#xff08;BST&#xff09;的根节点 root &#xff0c;找出并返回 BST 中的所有 众数&#xff08;即&#xff0c;出现频率最高的元素&#…
阅读更多...
PROJ 9.1.1源码下载编译（Win10+VS2022）

PROJ 9.1.1源码下载编译（Win10+VS2022）

目录PROJ什么是PROJPROJ下载方式资源结构编译PROJ打包编译成功的库PROJ 什么是PROJ Proj是一个免费的GIS工具。 它专注于地图投影的表达&#xff0c;以及转换。采用一种非常简单明了的投影表达PROJ&#xff0c;比其它的投影定义简单&#xff0c;但很明显。很容易就能看到各种…
阅读更多...
无人机倾斜摄影测量技术的优势有哪些？

无人机倾斜摄影测量技术的优势有哪些？

传统的地理信息获取工作一般是通过人工测量的方式进行&#xff0c;但这样的测量方式具有工作强度大、成本高等问题。随着现代科技的不断发展&#xff0c;测绘行业对地理信息数据的准确性、时效性要求也越来越高&#xff0c;人工成本和时间成本也为行业带来了巨大的压力。因此&a…
阅读更多...
GIT回退到指定版本的两种方法（reset/revert）

GIT回退到指定版本的两种方法（reset/revert）

实现多人合作程序开发的过程中&#xff0c;我们有时会出现错误提交的情况&#xff0c;此时我们希望能撤销提交操作&#xff0c;让程序回到提交前的样子&#xff0c;本文总结了两种解决方法&#xff1a;reset、revert。 命令特点reset该命令会强行覆盖当前版本和要回退的版本之…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023