一、题目

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1：

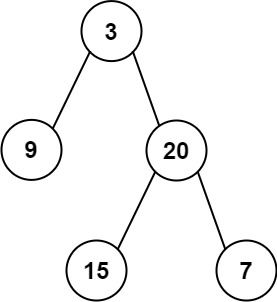
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2：
输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示：

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均无重复元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列

二、代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    // 优化算法，将原本每一次调用都要遍历一遍找到find的操作，变成总总共只需要遍历一次，存入数组中，以后再去取find直接从数组中就可以获取到，不用便利了，这样整个复杂度变成了O(N)
    public static TreeNode buildTree(int[] pre, int[] in) {
        if (pre == null || in == null || pre.length != in.length) {
            return null;
        }

        // 创建一个Map用来存放中序遍历中每一个值所在的位置
        HashMap<Integer, Integer> valueIndexMap = new HashMap<>();
        for (int i = 0; i < in.length; i++) {
            valueIndexMap.put(in[i], i);
        }

        // 调用递归
        return g(pre, 0, pre.length - 1, in, 0, in.length - 1, valueIndexMap);
    }

    // 有一棵树，先序结果是pre[L1...R1]，中序结果是in[L2...R2]
    // 请建出整棵树返回头节点

    // 这个思路就是根据中序根节点左边是其左子树，右边使其右子树，然后前序遍历每一段的最开始节点一定是根节点。通过这个特点来构造出整个二叉树
    // 关键是找到递归出口
    public static TreeNode g(int[] pre, int L1, int R1, int[] in, int L2, int R2,
                             HashMap<Integer, Integer> valueIndexMap) {

        // 这种情况当前节点已经没有左右子节点了，这个时候如果还按照递归的写法L1 + 1，就会导致得到的数已经超过了有边界，这种情况说明遍历到了最底层的空节点，直接返回空
        if (L1 > R1) {
            return null;
        }

        // 递归出口，当先序遍历递归到了只剩下一个节点，说明这个肯定是一个根节点，返回。这里是所有递归返回的开始，从这里开始，这一个分支的递归就不会再向下一层继续了，而是还是向上层返回。因为这个返回位置在继续向下递归调用的方法代码的前面。
        TreeNode head = new TreeNode(pre[L1]);
        if (L1 == R1) {
            return head;
        }

        // 找到当前节点在中序遍历中的位置，用来分割左右子树
        int find = valueIndexMap.get(pre[L1]);
        // 先通过中序遍历获取一下下一层递归所涉及到的数组范围，左子树就是L2~find - 1
        // 这样我们就知道总共涉及到find - 1 - L2个元素，这样先序遍历设计的范围就是，L1+1 ~ L1 + 1 + find - 1 - L2，这样就把这一段子树的左右子节点都涵盖进去了
        head.left = g(pre, L1 + 1, L1 + find - L2, in, L2, find - 1, valueIndexMap);
        // 右子树递归同理
        head.right = g(pre, L1 + find - L2 + 1, R1, in, find + 1, R2, valueIndexMap);

        // 走到这一步直接返回当前根节点，将每一层当前的节点都向上一层返回，这样才这逐层构建出二叉树结构。这一步就是连接每一层递归的接口，用来将下层结果数据传递给上一层，逐层传递，返回到最上层时最终得到结果
        return head;
    }
}