目录
二叉搜索树的众数
二叉树的最近公共祖先
修剪二叉树
二叉搜索树的众数
问题描述:
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。如果树中有不止一个众数,可以按 任意顺序 返回。
思路1:运用STL中的容器map,vector来辅助解决。通过遍历二叉树,将其放入map中,map可以统计每个key对应的value值。但map是对key排序的,所以再将每个键值对放入vector中,让vector对value值进行排序。
对应代码:
class Solution {
public:
map<int,int> m_;
void _preoder(TreeNode* root)
{
if(root==nullptr)
return;
if(root!=nullptr)
m_[root->val]++;
_preoder(root->left);
_preoder(root->right);
}
bool static cmp(const pair<int,int>&a,const pair<int,int>& b)
{
return a.second>b.second;//按从大到小排序
}
vector<int> findMode(TreeNode* root) {
_preoder(root);
vector<pair<int,int>> v_(m_.begin(),m_.end());
sort(v_.begin(),v_.end(),cmp);
vector<int> result;
result.push_back(v_[0].first); //其中一个众数
for(int i=1;i<v_.size();i++)
{
if(v_[i].second==v_[i-1].second)// 可能有多个众数
result.push_back(v_[i].first);
else
break;
}
return result;
}
};思路2:因为是二叉搜索数,所以按中序遍历的顺序去遍历时,是按从小到大的顺序访问的,可以去比较相近的两个元素是否相等,统计最大的次数。
中序遍历的框架与上文介绍的是一样的:
TreeNode* pre=nullptr;
void _findMode(TreeNode* cur)
{
if(cur==nullptr)
return;
_findMode(cur->left);
if(pre==nullptr)
cur=pre;
else
//处理节点
_findMode(cur->right);
}用两个变量分别记录当前遍历到的元素个数,和当前最多的元素的个数。将出现最多的元素放入vector中。例如:
class Solution {
public:
TreeNode* pre=nullptr;
vector<int> result;
int count=0;
int maxcount=0;
void _findMode(TreeNode* cur)
{
if(cur==nullptr)
return;
_findMode(cur->left);
if(pre==nullptr) //若pre为空,则cur刚找到最小的元素,此时count置位1
count=1;
else if(pre->val==cur->val) //前后两元素相同,则count++
count++;
else //重新计数
count=1;
pre=cur;
if(count==maxcount) //说明出现了多个相同次数的元素
result.push_back(cur->val);
if(count>maxcount) //后面出现的元素次数更大,把之前加入的元素清空,重新加入
{
result.clear();
result.push_back(cur->val);
maxcount=count;
}
_findMode(cur->right);
}
vector<int> findMode(TreeNode* root) {
TreeNode* cur=root;
_findMode(cur);
return result;
}
};这种方法只需要遍历一次二叉树即可。
二叉树的最近公共祖先
题目描述:给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大
思路1:分别寻找p,q是在当前的节点的左边还是右边。因为题目给定的p,q两个节点必定存在公共祖先。情况1:当前节点就是p或者q,那么当前节点就是祖先。情况 2:p,q分别在当前节点的两边,那么当前节点就是祖先。情况3:p,q节点都在当前节点的左边或者右边,那么当前节点往左或者右边遍历,重复上面的的操作。
class Solution {
public:
bool _istree(TreeNode*root,TreeNode*node) //确定p,q节点是否在当前节点下
{
if(root==nullptr)
return false;
if(node==root)
return true;
return _istree(root->left,node)||_istree(root->right,node);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(p==root||q==root)
return root;
bool pinleft=_istree(root->left,p);
bool pinright=!pinleft;
bool qinleft=_istree(root->left,q);
bool qinright=!qinleft;
if((pinleft&&qinright)||(pinright&&qinleft))
return root;
else if(pinleft&&qinleft)
return lowestCommonAncestor(root->left,p,q);
else if(pinright&&qinright)
return lowestCommonAncestor(root->right,p,q);
else
{}
return nullptr;
}
};上面的思路很好理解,但是若p,q节点都是叶子节点,都是兄弟节点。那么上面的代码时间复杂度就会很高。 (lowestCommonAncestor)每往后走一步,(_istree)都要遍历到最后才能找到,(lowestCommonAncestor)也要走到最后,就是p,q的父亲节点才能结束。
思路2:若是可以通过自底向上去查找就更容易了,可以模拟二叉树后序遍历的过程。把找到的结果返回给上一层。
例如:
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root==nullptr||root==p||root==q)//终止条件
return root;
TreeNode* left=lowestCommonAncestor(root->left,p,q);
TreeNode* right=lowestCommonAncestor(root->right,p,q);
if(left!=nullptr&&right!=nullptr) //找到了结果,返回
return root;
else if(left==nullptr&&right==nullptr)
return nullptr;
else if(left!=nullptr)
return left;
else
return right;
}
};思路3:从头节点开始,找到每个节点的路径,然后再去找到路径上的共同节点。
class Solution {
public:
bool findpath(TreeNode* root,TreeNode* x,stack<TreeNode*>& Path)
{
if(root==NULL)
return false;
Path.push(root);
if(root==x)
return true;
if(findpath(root->left,x,Path))
return true;
if(findpath(root->right,x,Path))
return true;
Path.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
stack<TreeNode*>ppath,qpath;
findpath(root,p,ppath);
findpath(root,q,qpath);
while(ppath.size()>qpath.size())
{
ppath.pop();
}
while(ppath.size()<qpath.size())
{
qpath.pop();
}
while(ppath.top()!=qpath.top())
{
ppath.pop();
qpath.pop();
}
return ppath.top();
}
};修剪二叉树
题目描述:给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案
思路:
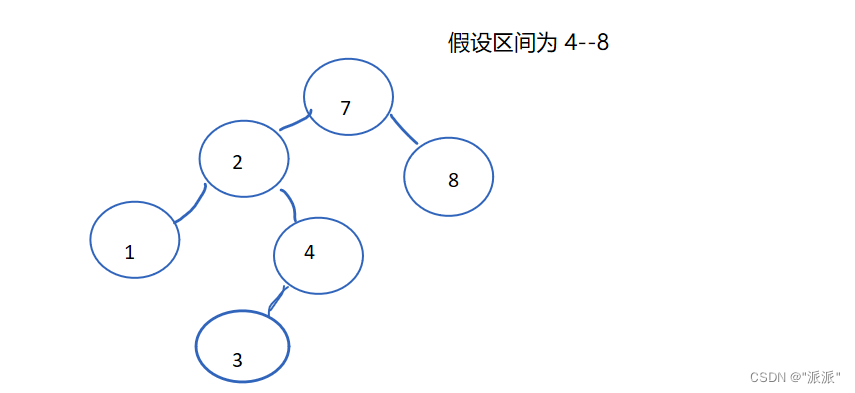
可能很容易写出这样的代码:直接判断当前节点是否满足条件,如不满足,这直接将左孩子或右孩子返回。
例如:
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if(root==nullptr)
return nullptr;
if(root->val<low)
return right;
if(root->val>high)
return left;
root->left=trimBST(root->left,low,high); //条件满足,则继续递归当前节点的左右孩子,对其修剪
root->right=trimBST(root->right,low,high);
return root; //返回当前节点给上一层
}
};这样的话并没有把节点值3给删除点,正确的做法是,例如当前节点的值已经小于low,那么它的右孩子也可能小于low或者它的右子树中有节点小于low.它的左子树肯定不满足条件了。后面要对它的右子树进行修建,接受它的右子树的返回值,再将结果返回给上一层。
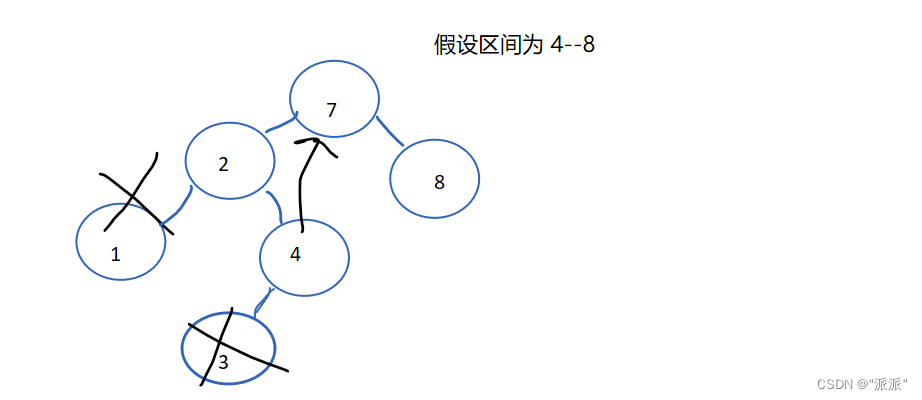
代码:
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if(root==nullptr)
return nullptr;
if(root->val<low)
{
TreeNode* right=trimBST(root->right,low,high); //对右子树进行修剪
return right; //当前节点已不满足条件,接收右子树返回值,再返回
}
if(root->val>high)
{
TreeNode* left=trimBST(root->left,low,high); //对左子树修剪
return left; //当前节点已不满足条件,接收左子树返回值,再返回
}
root->left=trimBST(root->left,low,high);//条件满足,则继续递归当前节点的左右孩子,对其修剪
root->right=trimBST(root->right,low,high);
return root; //返回当前节点给上一层
}
};