目录
链式二叉树的实现:
前提须知:
前序:
中序:
后序:
链式二叉树的构建:
定义结构体:
初始化:
构建左右子树的指针指向:
前序遍历的实现:
中序遍历的实现:
后序遍历的实现:
求二叉树结点个数:
写法1:
写法2:
求树的叶子结点个数:
求树的高度:
求第K层结点:

链式二叉树的实现:
前提须知:
链式二叉树的实现主要服务于那些不能被数组存储的非满二叉树和非完全二叉树,而在这些二叉树中,我们又将它们的组成结构进行拆分,分别是根、左子树、右子树。
而左子树和右子树又可以根据该结构划分为它们的根、左子树、右子树。

前序:
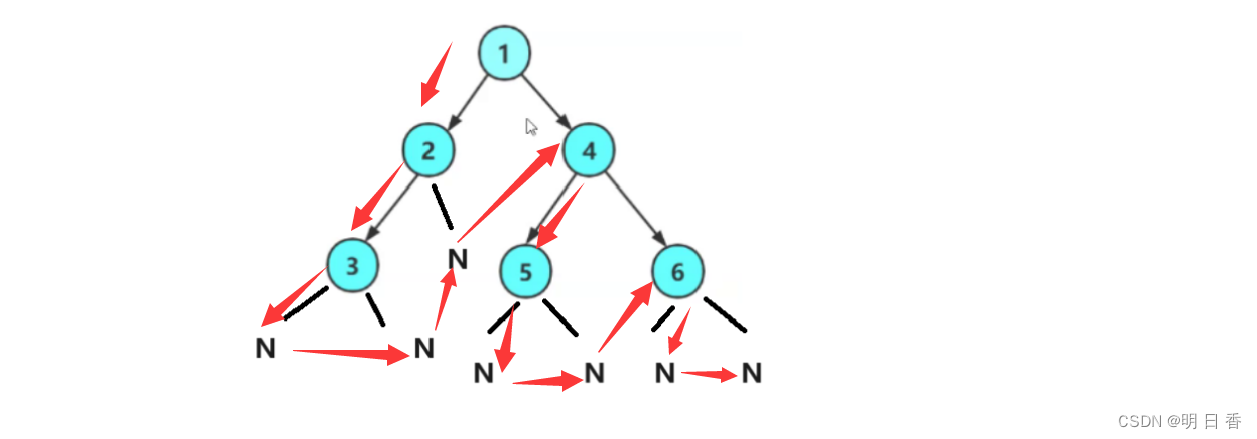
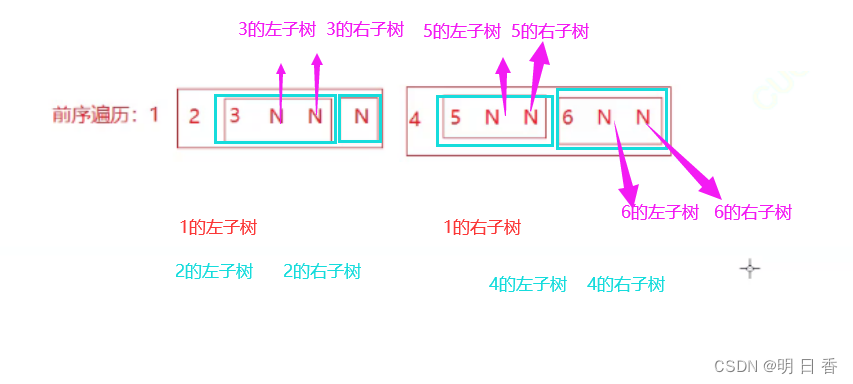
是将二叉树以根、左子树、右子树顺序进行结构划分遍历的遍历方式。
如图所示:其中N表示结点是NULL
以数字表示为:1 2 3 N N N 4 5 N N 6 N N
中序:
是将二叉树以左子树、根、右子树顺序进行结构划分遍历的遍历方式。
如图所示:其中N表示结点是NULL
以数字表示为N 3 N 2 N 1 N 5 N 4 N 6 N
后序:
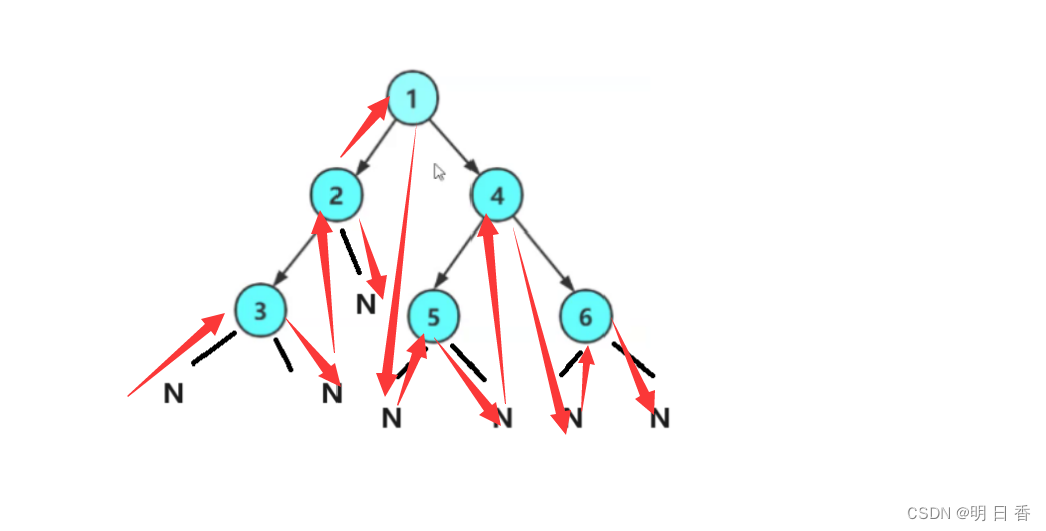
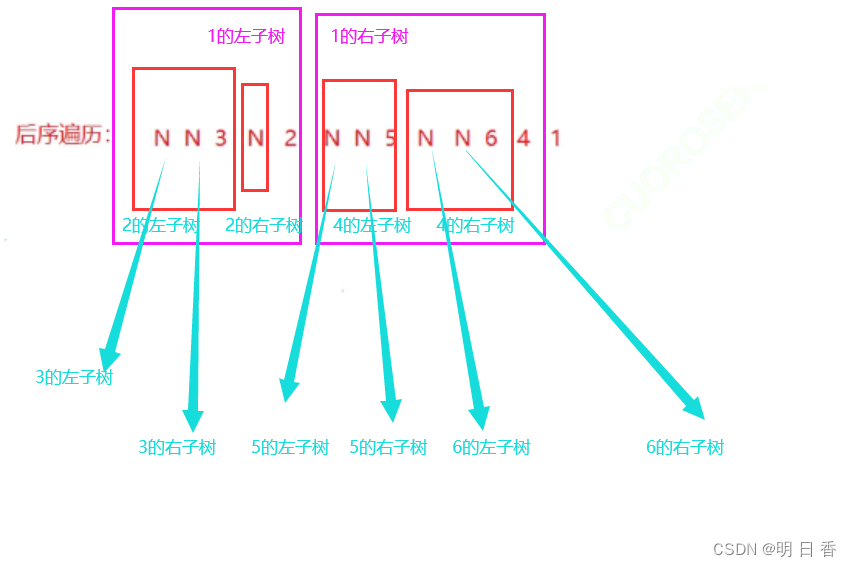
是将二叉树以左子树、右子树、根顺序进行结构划分遍历的遍历方式。
如图所示:其中N表示结点是NULL
以数字表示为N N 3 N 2 N N 5 N N 6 4 1
链式二叉树的构建:
万恶之源~递归!

定义结构体:
一个链式二叉树,需要有存放结点元素的data、需要有两个分别指向左子树、右子树的指针。
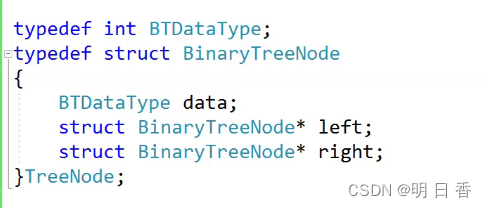
初始化:
开辟空间构建结点:
记得将构建的结点的左右子树指针进行初始化,以及结点元素进行赋值。

构建左右子树的指针指向:
构建的结点如上图的二叉树结构所示。

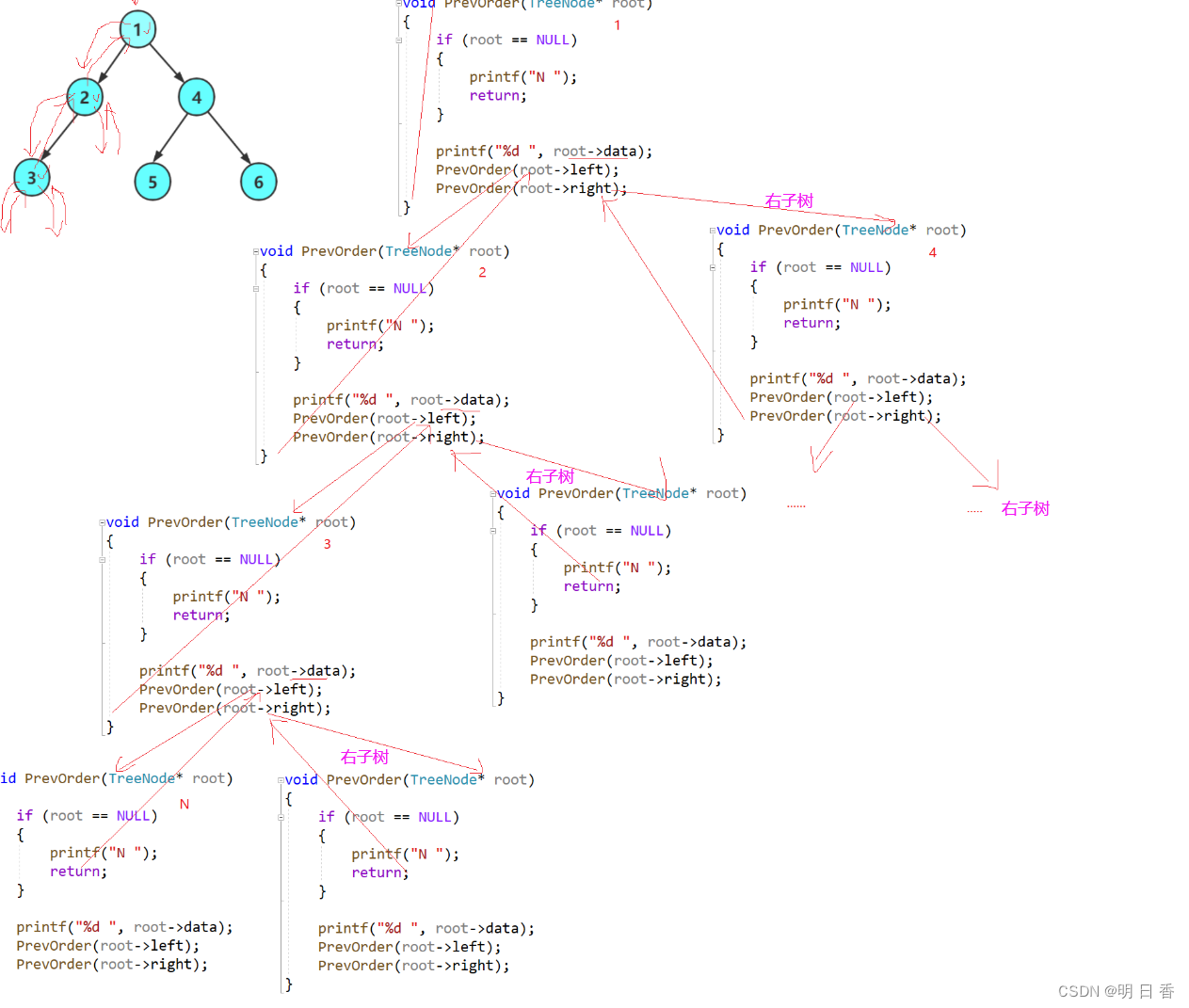
前序遍历的实现:

前序遍历的思路是,根、左子树、右子树,所以先要打印根,在前往根的左子树,而根的左子树又可以进行前序的遍历,因此使用递归的思想,先不断地进行调用以此抵达最左边的结点,随后逐级的递归,然后再迈向右子树进行相同的操作,也就是调用进入左子树,然后逐级递归……
二叉树走向图

代码调用思路图
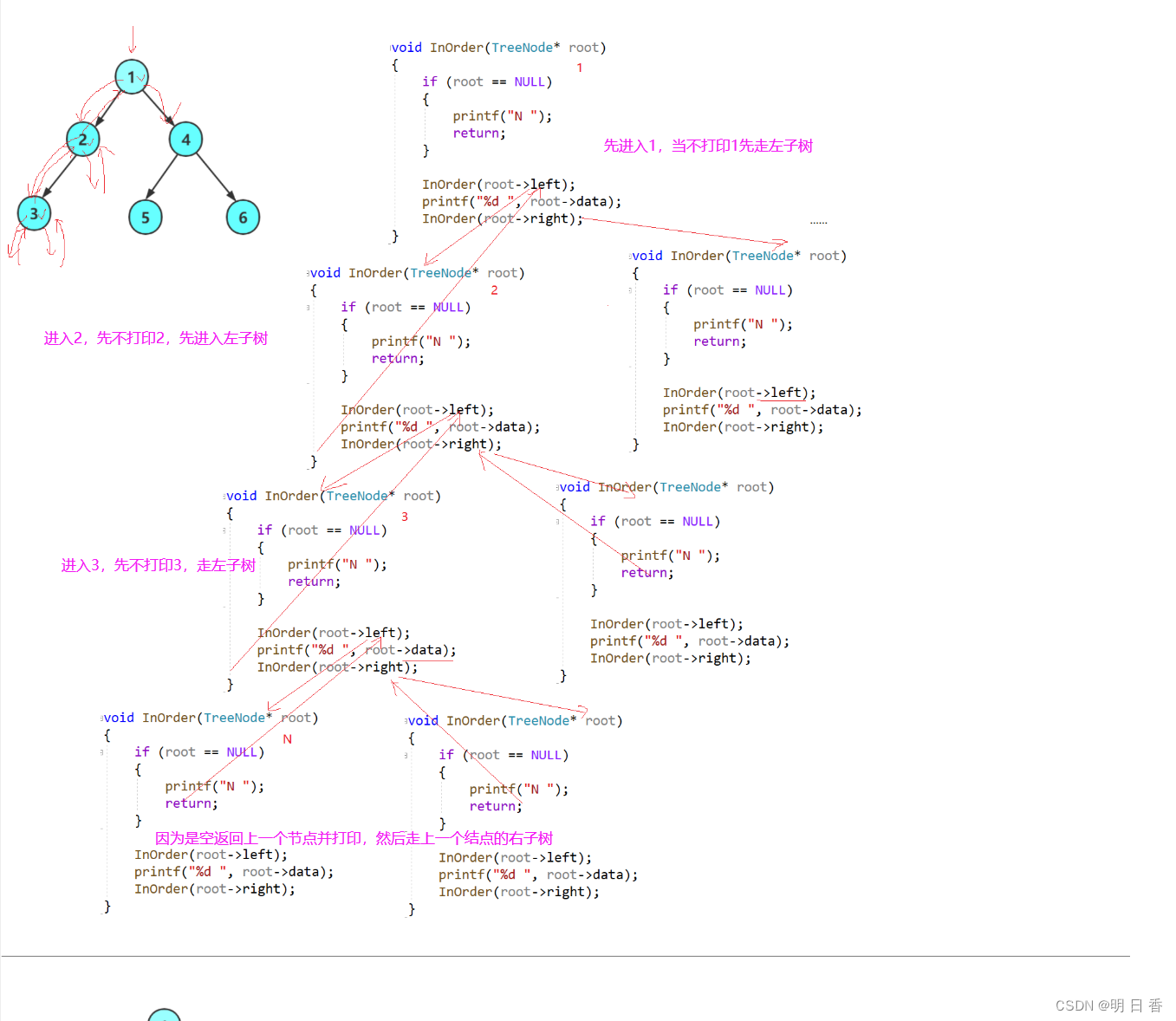
中序遍历的实现:

中序的遍历思想是左子树、根、右子树,所以再打印上是先打印左子树而后再打印根结点,最后再打印右子树,所以利用递归的思想,想要遍历到最左的结点,之后打印,随后进入右子树中,接着遍历左子树,以此类推……
二叉树走向图

代码思路调用图
后序遍历的实现:
后序就是中序的指向右子树和打印结点子树互换顺序即可
求二叉树结点个数:
用递归的思想,将问题化解为左子树的结点个数+右子树的结点个数+根结点的结点个数。
- 而左右子树的结点个数又可以划分为左子树的结点个数+右子树的结点个数+根结点的结点个数。
- 因此,本题就可以变为如果当前结点不是NULL那++size,如果是NULL则返回return。
- 而再递归中return 也仅仅只是跳出了这一回的进程,返回上一次调用的进程并进入下一条代码中。
写法1:
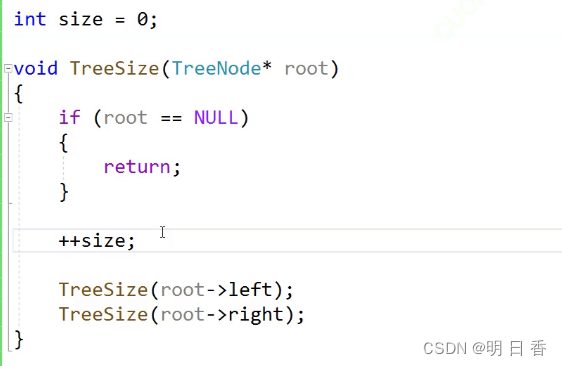
图解

写法2:
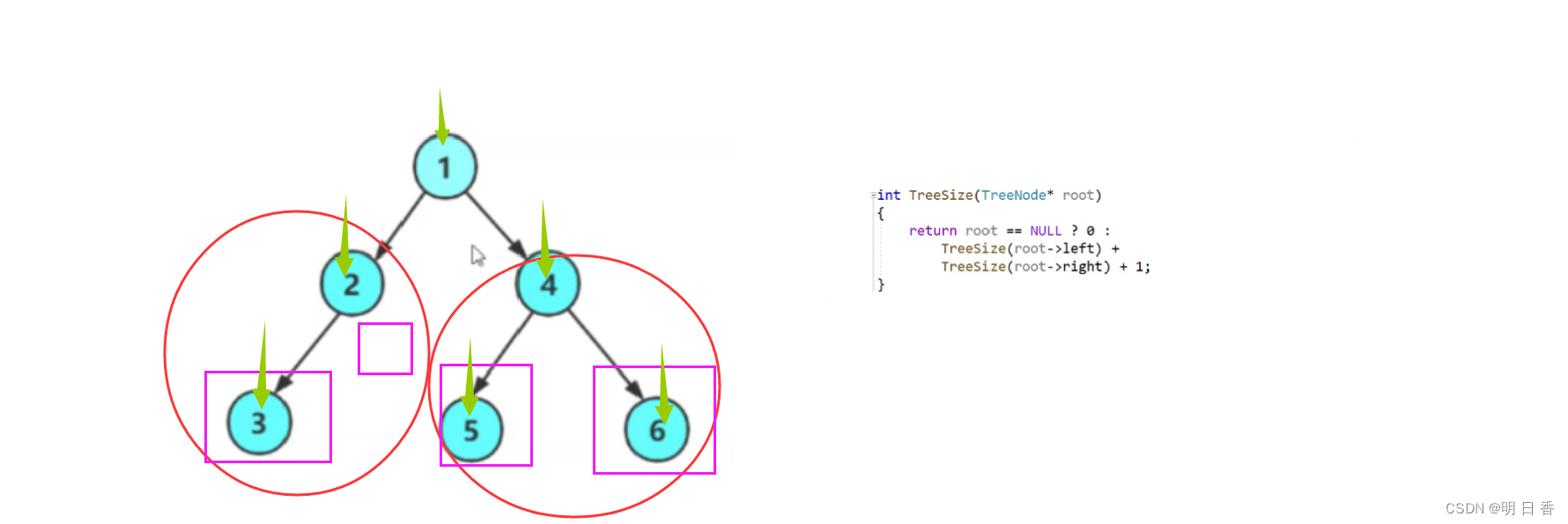
写法2就是彻底的简化了写法1,使用了三目运算符,将++size问题彻底变为了1的累加。
如果root = NULL 则返回0,如果不等于NULL 则进行调用 进入左子树的递归调用和右子树的递归调用

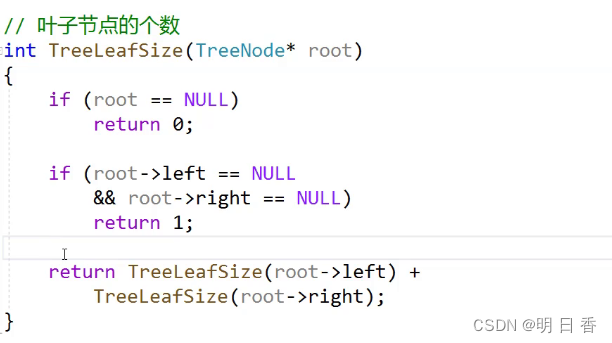
求树的叶子结点个数:
叶子结点概念:树与二叉树堆:树-CSDN博客
该问题的核心可以拆分为 树的叶子结点个数 = 左子树叶子结点个数+右子树叶子结点个数
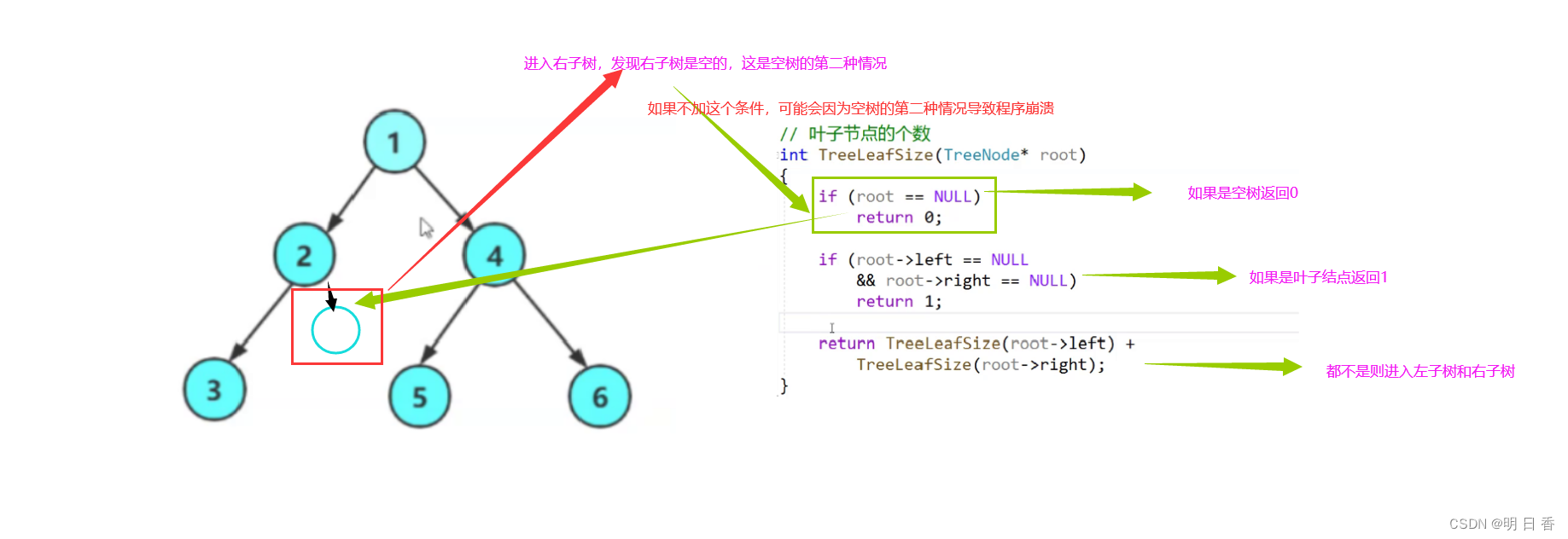
本问题其实是上一个问题的进阶版本,本质上多了两个条件,也就是当结点的左右子树指针指向的是NULL时便返回1,表示该节点是叶子节点,而非叶子节点则进入调用,分别进入结点的左右子树进行递归调用,知道root == NULL 或者是叶子节点,进行return 返回上一个结点开始逐级返回……
求树的高度:
本问题可以转化为求树的高度是左子树、右子树二者中高度最大的+1 ,这个1是根结点,由此可以化为1的累加问题。
也便是通过 root == NULL 进行逐级的返回,和+1来达成1的累加。

- 如上代码所示,进入了最左边的结点后,以root == NULL 为返回条件
- 当最左边结点的左子树的leftheight因为root == NULL 返回0, 结束后返回到了上一个结点(最左结点),并进入了该结点(最左结点)的右子树
- 随后右子树又以root == NULL 返回后,进入两个子树的高度对比
- 因为NULL 所以这里的两个返回值是 0 +1 和 0 + 1 进行对比,所以最后返回1 到本结点(最左结点)的上一个节点 (最左结点的父亲结点)

使用特殊函数进行比较

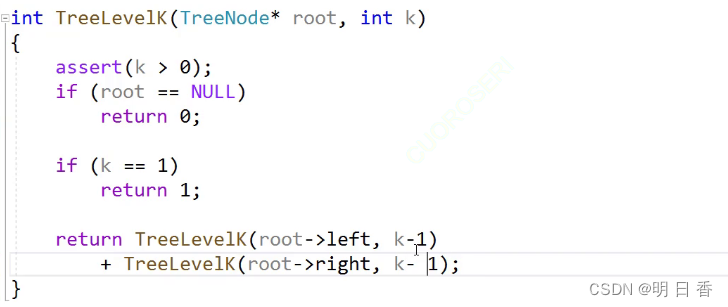
求第K层结点:
假设,如果再根节点是求第K层,那么再根结点的左右子树的根结点来看是k-1层
- 又因为 条件 root ==NULL 表示树是空的,所以返回0,而k == 1表示树只有一个根结点,所以只有一个结点
- 又因为树可以拆分左右子树和根,而左右子树又可以继续拆分,而又是求第K层的结点个数,所以可以通过K==1这个条件进行返回进行回代数值。
- 也因此可以使用k>1和k-1进行不断地调用到第K层,然后进行回代返回值
注意,是带回返回值,而不是将返回值进行累加
思路图