难度:简单
给你一个正整数
n,开始时,它放在桌面上。在109天内,每天都要执行下述步骤:
- 对于出现在桌面上的每个数字
x,找出符合1 <= i <= n且满足x % i == 1的所有数字i。- 然后,将这些数字放在桌面上。
返回在
109天之后,出现在桌面上的 不同 整数的数目。注意:
- 一旦数字放在桌面上,则会一直保留直到结束。
%表示取余运算。例如,14 % 3等于2。示例 1:
输入:n = 5 输出:4 解释:最开始,5 在桌面上。 第二天,2 和 4 也出现在桌面上,因为 5 % 2 == 1 且 5 % 4 == 1 。 再过一天 3 也出现在桌面上,因为 4 % 3 == 1 。 在十亿天结束时,桌面上的不同数字有 2 、3 、4 、5 。示例 2:
输入:n = 3 输出:2 解释: 因为 3 % 2 == 1 ,2 也出现在桌面上。 在十亿天结束时,桌面上的不同数字只有两个:2 和 3 。提示:
1 <= n <= 100
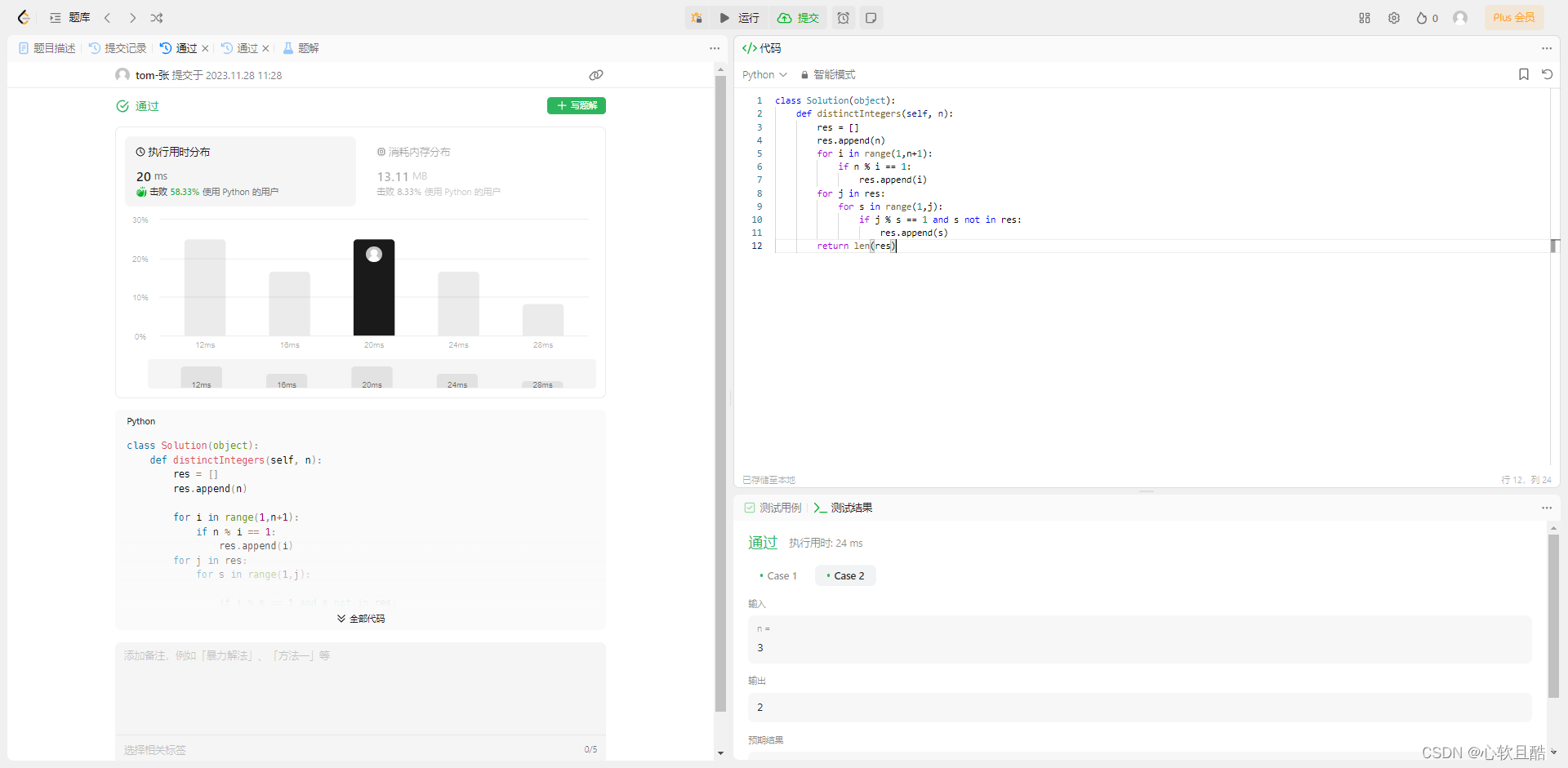
题解:class Solution(object): def distinctIntegers(self, n): res = [] res.append(n) for i in range(1,n+1): if n % i == 1: res.append(i) for j in res: for s in range(1,j): if j % s == 1 and s not in res: res.append(s) return len(res)
leetcode:2549. 统计桌面上的不同数字(python3解法)
news2026/2/13 19:45:17
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1265351.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
链接1:编译器驱动程序
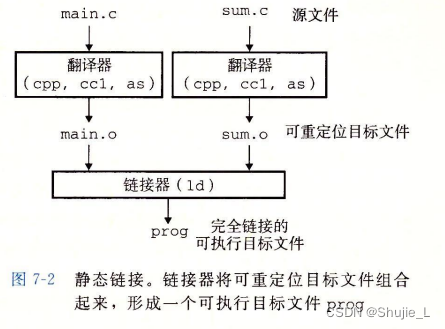
文章目录 GNU编译器示例编译 GNU编译器
GNU编译器(GNU Compiler)是由自由软件基金会(Free Software Foundation,FSF)开发和维护的一套编译器集合。这些编译器主要用于编译各种编程语言的源代码,将其转换为…
汽车电子 -- 车载ADAS之FCW(前方碰撞预警)
相关法规文件:
FCW: GB∕T 33577-2017 智能运输系统 车辆前向碰撞预警系统 性能要求和测试规程
一、前方碰撞预警 FCW( Forward Collision Warning)
参看:法规标准-GB/T 33577标准解读(2017版)
1、状态机 系统关闭 当车辆前向碰撞预警系…
08-学成在线项目中统一异常处理的规范
项目中的异常处理
规范异常类型
在Service类的业务方法中有很多的参数合法性校验,当请求参数不合法的时候会抛出异常,但此时异常信息只会在控制台输出,前端界面并不会提示用户
实际开发中前端和后端需要做一些约定: 一般将错误提示信息统一以json格式返回给前端,以HTTP状态码…
excel表格在线编辑(开源版)
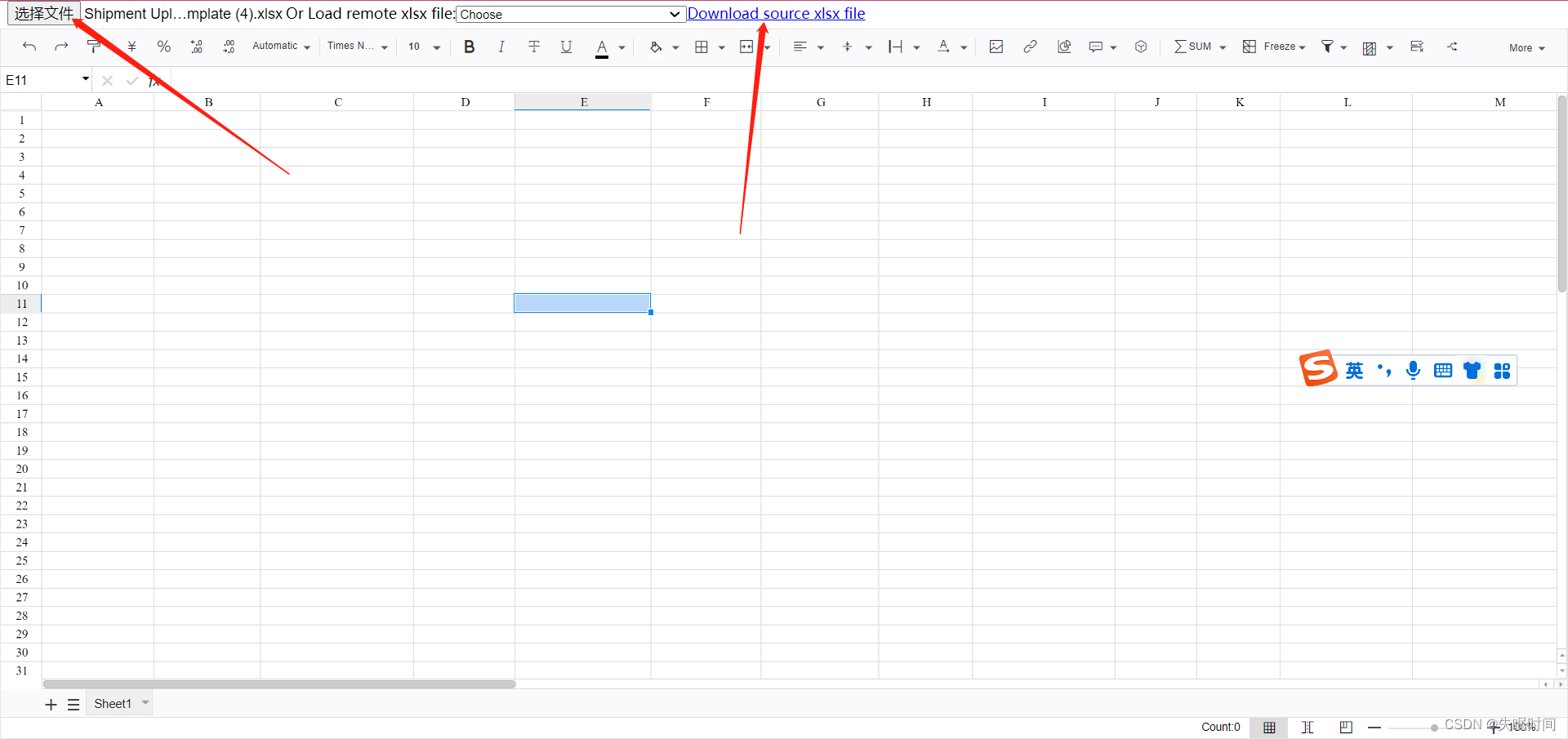
文章目录 前言一、Luckysheetvue3vite 例子如有启发,可点赞收藏哟~ 前言
本文记录好用的开源在线表格 具体如图显示 另外记录下更名后的univer~,如下图(有兴趣可自行详细了解) univer
在线思维导图 一、Luckysheet
参考git…
【LeetCode】每日一题 2023_11_28 设计前中后队列(数组/链表/双端队列)
文章目录 刷题前唠嗑题目:设计前中后队列题目描述代码与解题思路偷看大佬题解 结语 刷题前唠嗑 LeetCode?启动!!!
这道题的难度,才是我想象中的中等题的难度好吧,昨天那玩意对我来说还是太难了…
WebUI自动化学习(Selenium+Python+Pytest框架)003
1.元素操作
在成功定位到元素之后,我们需要对元素进行一些操作动作。常用的元素操作动作有:
(1)send_keys() 键盘动作:向浏览器发送一个内容,通常用于输入框输入内容或向浏览器发送快捷键
(2…
C语言——有一个3*4的矩阵,要求求出其中值最大的那个元素的值,以及其所在的行号和列号
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>
int main()
{int i,j,row0,colum0,a[3][4]{{1,2,3,4},{9,8,7,6},{-10,10,-5,2}};int maxa[0][0];for ( i 0; i < 3; i)//行(row){for ( j 0; j < 4; j)//列(colum…
【FGPA】Verilog:JK 触发器 | D 触发器 | T 触发器 | D 触发器的实现
0x00 JK 触发器
JK 触发器是 RS 触发器和 T 触发器的组合,有两个输入端 J 和 K,如果两个输入端都等于 1,则将当前值反转。 行为表 状态图 Timing Diagram Circuit
JK 触发器的设计目的是防止 RS 触发器在输入 S 和 R 均等于 …
Unity学习笔记11
一、视频播放功能
1.如何让视频在游戏场景中播放?
在Assets目录下添加一个渲染器纹理,步骤:新建→渲染器纹理 首先在创建一个平面,想让视频在平面上显示。在平面上添加一个组件 Video Player 然后将视频文件拖拽到视频剪辑位置上…
网络安全--基于Kali的网络扫描基础技术
文章目录 1. 标准ICMP扫描1.1使用Ping命令1.1.1格式1.1.2实战 1.2使用Nmap工具1.2.1格式1.2.2实战1.2.2.1主机在线1.2.2.2主机不在线 1.3使用Fping命令1.3.1格式1.3.2实战 2. 时间戳查询扫描2.1格式2.2实战 3. 地址掩码查询扫描3.1格式3.2实战 2. TCP扫描2.1TCP工作机制2.2TCP …
IDEA编译器的永久试用设置与基本使用
参考视频: 最通俗易懂的JDK、IDEA的安装使用权威指南 2023新版前端Web开发HTML5CSS3移动web视频教程,前端web入门首选黑马程序员 文章目录 一.安装包下载与安装二.设置IDEA永久试用三.IDEA的基本试用0.IDEA管理Java程序的结构1.工程创建2.模块创建3.包创…
【Java】使用 IDEA 快速生成 SpringBoot 模块
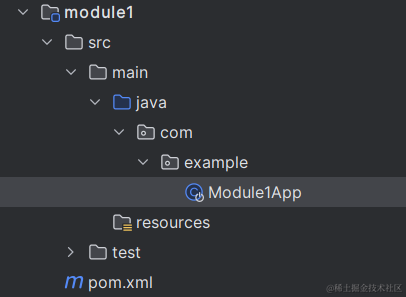
项目目录下新建 module 模块 在 pom.xml 更改为 spring initializr 配置之后的 pom.xml <?xml version"1.0" encoding"UTF-8"?>
<project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchem…
yolov8-seg 分割推理流程
目录
一、分割检测
二、图像预处理
二、推理
三、后处理与可视化
3.1、后处理
3.2、mask可视化
四、完整pytorch代码 一、分割检测
注:本篇只是阐述推理流程,tensorrt实现后续跟进。
yolov8-pose的tensorrt部署代码稍后更新,还是在仓…
如何根据接口文档,轻松快速的模拟接口服务?
什么是WireMock?
WireMock 是一个Http 模拟服务,其核心也是一个web服务,WireMock主要是为特定请求提供固定的返回值。
WireMock可以作为单独进程启动,模拟一个WEB服务器,提供一些API访问,并返回特定的返回值。也可以作为第三方库在项目中使用。
如何使用
standalone方…
csdn博客编写技巧
随便记录一下csdn博客编写时候用的到技巧,以作备忘。 1. 表格
1.1 Markdown-Table-Generator
这个是csdn编辑器中,工具栏自带的表格用法。主要优点是比较直观,缺点是无法设置表格中行列的宽高。
用法:
| 表头一 | 表头二 |
|-…
Vue基本使用(一)
📑前言
本文主要是【Vue】——Vue基本使用的文章,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是听风与他🥇 ☁️博客首页:CSDN主页听风与他 🌄每日一句&#x…
【CAD二次开发】标注箭头,获取修改标注箭头图块
常见的的标注箭头有以下种类 public static List<string> ArrowBlock = new List<string>(){" ","_CLOSEDBLANK&
淘宝API接口系列:连接商户与消费者的桥梁
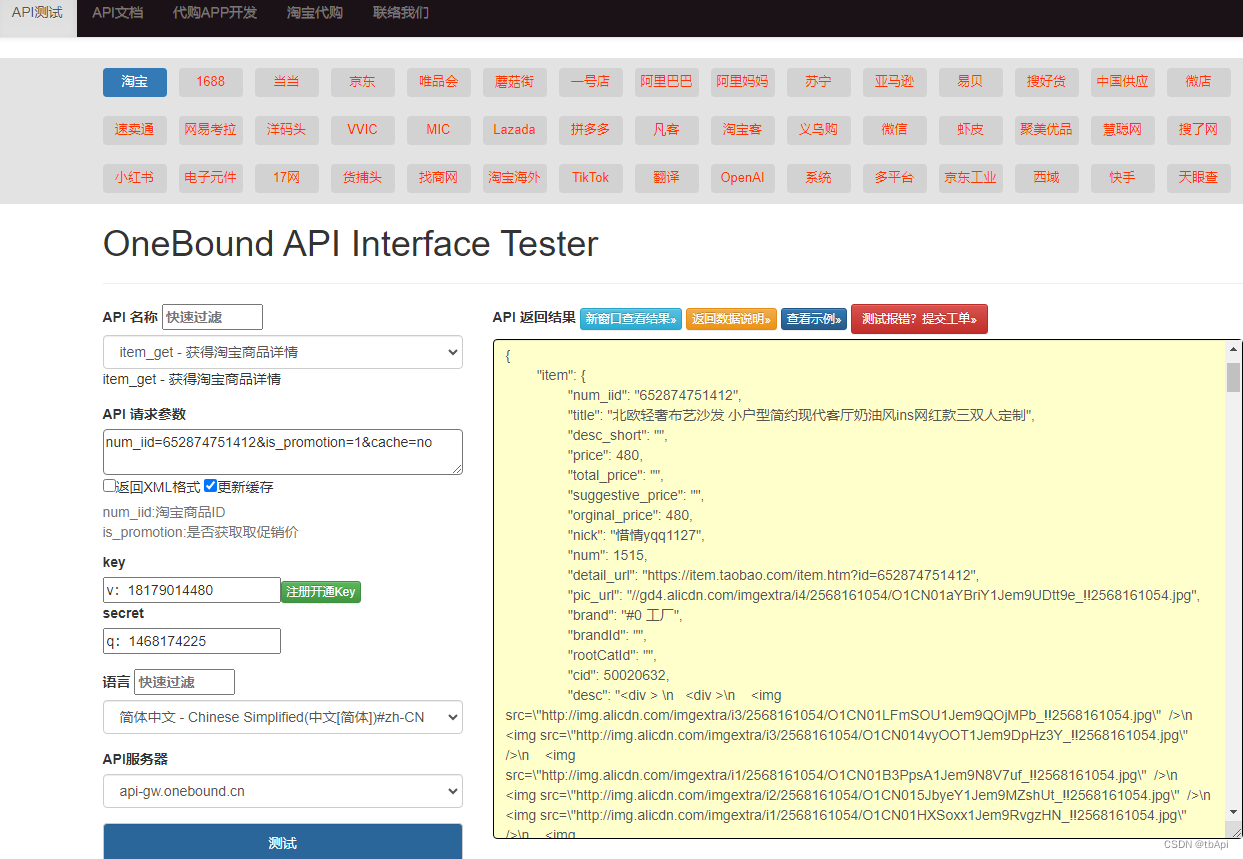
一、引言
淘宝,作为中国最大的电商平台之一,拥有数以亿计的注册用户和海量的商品信息。淘宝API接口作为连接商户与消费者的重要桥梁,为开发者提供了丰富的电商资源,帮助他们创新和优化业务。本文将深入探讨淘宝API接口的相关知识…