贪心算法（新坑）

news2025/1/9 17:46:49

贪心入门

概述：

贪心算法是一种在每一步选择中都采取当前最优解的策略，希望最终能够得到全局最优解的算法。简单来说，它会不断地做出局部最优的选择，相信通过这种选择最终能够达到全局最优。

举个例子来说明。假设你要从一个迷宫的起点走到终点，每个格子都有一个代价，你要找到一条路径，使得总代价最小。贪心算法会在每一步选择下一步的格子时，选择代价最小的格子，然后继续向着终点移动。这样每一步都选择当前最优的格子，最终就能够找到一条总代价最小的路径。（）

不过需要注意的是，贪心算法并不一定能够得到全局最优解，因为它只考虑当前步骤的最优选择，并没有考虑整体的情况。所以在应用贪心算法时，需要仔细分析问题的特征，确保贪心策略适用，并且通过数学证明或实验验证来证明其正确性。

举个简单的例子

有一堆钞票，你可以拿走十张，如果想达到最大的金额，你要怎么拿？

指定每次拿最大的，最终结果就是拿走最大数额的钱。

即每次拿最大的就是局部最优，最后拿走最大数额的钱就是推出全局最优。

贪心算法一般分为如下四步：

将问题分解为若干个子问题
找出适合的贪心策略
求解每一个子问题的最优解
将局部最优解堆叠成全局最优解

（过于理想化）

引入例题：

分发饼干

若干个子问题就是每个饼淦要怎么分。

最优的是大饼干分给胃口大的，能一口吃饱，或者从小的开始，小饼干喂饱小的，能一口吃饱。

全局最优就是喂饱尽可能多的小孩。

即：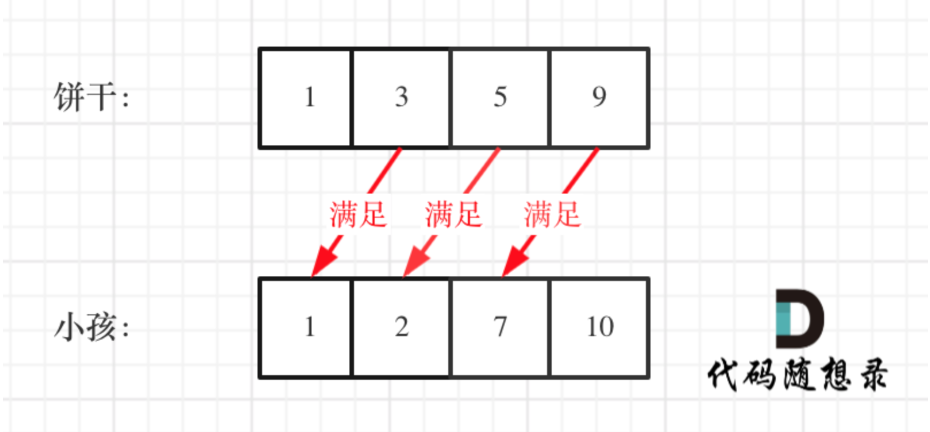

java：

class Solution {
    // 思路1：优先考虑饼干，小饼干先喂饱小胃口
    public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(g);
        Arrays.sort(s);//从小到大排序
        int start = 0;
        int count = 0;
        //嘴不变，饼干变
        for (int i = 0; i < s.length && start < g.length; i++) {//意思是胃口大就换大一点的饼干，小饼干就直接不要了
            if (s[i] >= g[start]) {
                start++;
                count++;
            }
        }
        return count;
    }
}