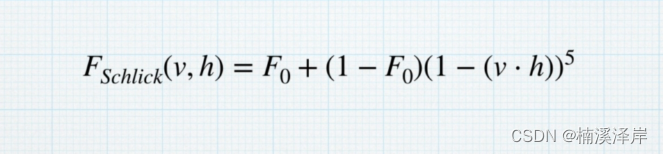目录
一、插入排序
1、插入排序的概念
2、插入排序的逻辑实现
3、插入排序的实现
二、希尔排序
1、希尔排序概念
2、希尔排序逻辑实现
3、间隔值(gap)对排序的影响
4、希尔排序的实现
三、插入排序与希尔排序性能对比测试
结语:
前言:
希尔排序的核心思想就是插入排序,他是在插入排序的基础上进行优化得来的,因此要想明白希尔排序的逻辑首先要认识插入排序。
一、插入排序
1、插入排序的概念
插入排序又名直接插入排序,其思想是把要插入的数值,插入到一个有序的序列中,从而得到一个新的有序序列。现实中就跟摸牌一样,每次摸一张牌都会把这张牌插入到手中牌堆的合适位置,从而让手里的牌变得有序。

2、插入排序的逻辑实现
排序的目的是让数组中的元素变得有序,比如冒泡排序的逻辑是从前往后遍历、相邻元素进行比较从而达到排序的功能。而插入排序的逻辑是从数组的最后一个元素往前遍历数组,举例:现如今要插入一个元素2,如果遇到大于2的元素则该元素往后“挪动”一位,直到遇到小于2的元素将2插入到该元素的后一位。
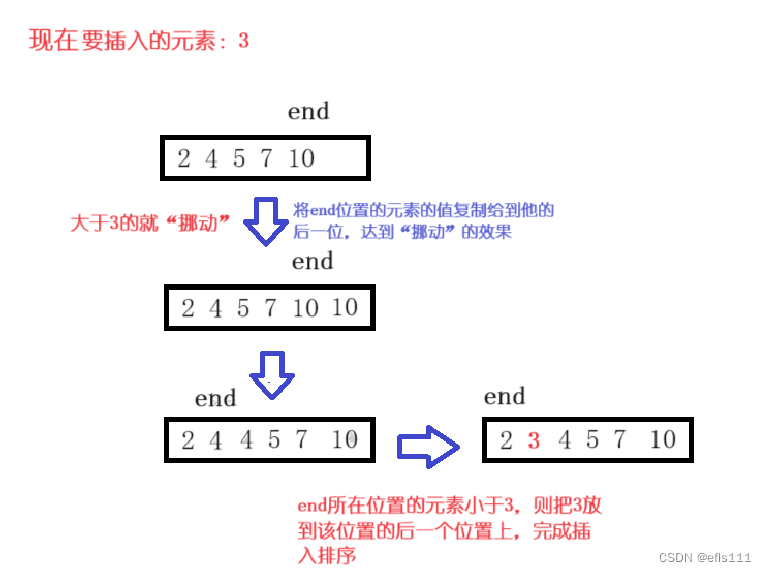
另一种情况就是当数组内的元素都比要插入的元素要大:
3、插入排序的实现
在明白插入排序的逻辑后,以下用代码的形式将插入排序实现,并且测试最终结果。
#include<stdio.h>
void InsertSort(int* a, int n)//插入排序
{
for (int i = 0; i < n - 1; i++)
{
int end = i;//表示当前数组的最后一个元素的下标
int temp = a[i + 1];//一般而言,把end后一个元素看作是要插入进行排序的元素
//因此为了防止该元素被end的元素所覆盖,因此要先保存起来
while (end >= 0)//end小于0说明数组内元素都大于该插入的元素
{
if (a[end] > temp)//大于插入元素的情况
{
a[end + 1] = a[end];//“挪动”
end--;//遍历end
}
else//小于或等于插入元素的情况
break;//直接跳出
}
a[end + 1] = temp;//不论大于还是小于插入元素,都把要插入的元素给到end位置的后一位
}
}
void PrintArr(int* a, int n)//打印数组
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
void Test_InsertSort()//插入排序测试函数
{
int arr[] = { 66,8,6,1,2,4,3,9 };
int sz = sizeof(arr) / sizeof(int);
PrintArr(arr, sz);
InsertSort(arr, sz);
PrintArr(arr, sz);
}
int main()
{
Test_InsertSort();
return 0;
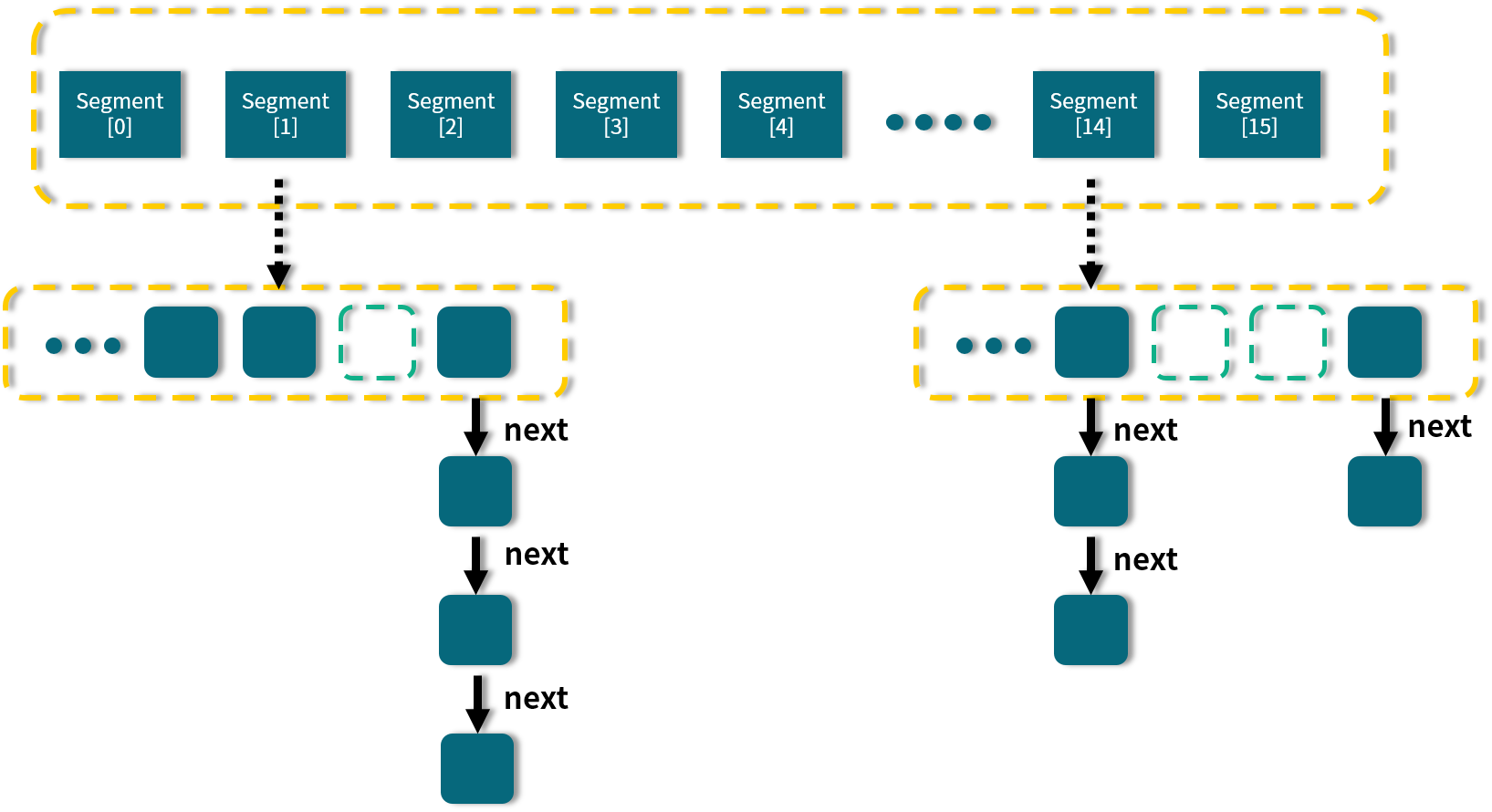
}其实在对数组进行插入排序时,都是在数组内进行操作的,实际上不存在“从外边来了一个元素”要插入这个数组,而是从数组的第二个元素开始,把第二个元素看成是“要插入”的元素进行插入排序的。示意图如下:

运行结果:

二、希尔排序
1、希尔排序概念
希尔排序是在插入排序的基础上进行优化而来的,因为插入排序如果是对一个比较有顺序的数组进行排升序,那么其时间复杂度是O(N),但是如果插入排序要把一个降序的数组排成升序,那么他的时间复杂度就等于O(N^2),而希尔排序优势就是在面对这种情况的时间复杂度依然可以做到O(N)。
希尔排序法又称缩小增量法,他的具体步骤可以分成两步:1、预排序,就是把要排序的数组按照某个间隔值分成若干个小数组。2、然后对这若干个数组进行插入排序。其中,让间隔值不断的缩小,直到间隔值为1时,希尔排序=插入排序,只不过在这个过程中希尔排序已经让数组变得有序了,所以哪怕最后希尔排序的效率=插入排序效率,总体而言希尔排序的效率是比插入排序要高的。详细如下文。
2、希尔排序逻辑实现
由于插入排序面对降序转升序的情况不好处理,因此介绍希尔排序的时候用一个降序的数组作为例子,现在要对一个降序的数组进行排升序,逻辑图如下:
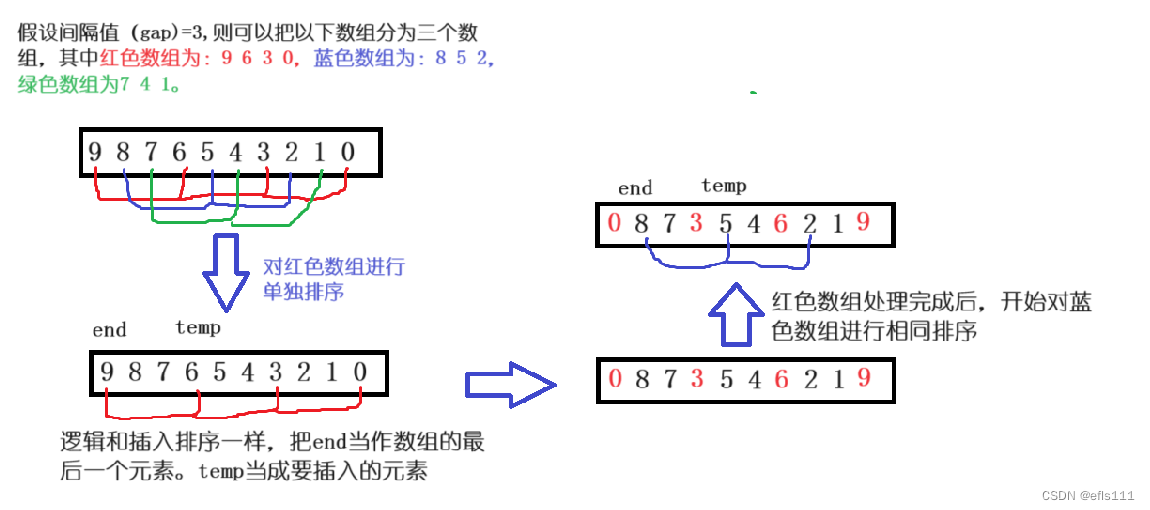
待到红、蓝、绿三个数组全部都排好之后,数组内顺序如下:

可以发现此时数组里的元素并不是一个升序状态,但是比处理前更接近升序了,这时候再对其进行插入排序则可以完成对该数组的升序排序,而且时间消耗也不大。
代码实现:
void ShellSort(int* a, int n)//希尔排序
{
int gap = 3;//假设gap=3
for (int j = 0; j < gap; j++)//控制小数组
{
for (int i = j; i < n - gap; i += gap)//对小数组进行排序
{
//插入排序的逻辑
int end = i;
int temp = a[end + gap];//注意小数组之间的间隔是gap
while (end >= 0)
{
if (a[end] > temp)
{
a[end + gap] = a[end];
end -= gap;
}
else
break;
}
a[end + gap] = temp;
}
}
}这里gap=3只能让该数组变得接近升序而不能排成升序,上文还提到了一个问题就是当gap=1时,希尔排序=插入排序,因此如果可以控制gap的值的变化,最后让gap=1就能完成对数组的升序排序了。那为什么gap=1时,希尔排序=插入排序呢,gap对排序的影响详细如下文。
3、间隔值(gap)对排序的影响
为什么间隔值gap=1的时候希尔排序=插入排序,从上文假设当gap=3,发现小数组中的元素与元素之间相隔了2个元素,那么gap=1时,元素与元素之间相隔0个元素,此时再对这些”小数组“进行排序实则就是对整个数组进行插入排序。

从上图可以得出,当gap=1时就是等价于插入排序的,那么gap=3、=5时会对数组里元素的顺序有什么影响吗,如下图所示:

可以发现当gap=1时,排出来的就是一个升序数组。
当gap=3时,排出来的结果接近升序数组。
当gap=5时,排出来的结果反而没那么接近升序了。
结论:当gap的值越大,则越不接近升序,当gap的值越小则越接近升序。但是gap值越大有一个好处是可以把数组中数值较大的元素挪到数组的后面,较小的值放到前面。因为间隔越大,则一次移动的步长就大。
但是gap一开始不能设置成1,不然希尔排序就没有意义了,希尔排序的优势是让gap>1的时候快速的把数组调成接近有序的,然后再用插入排序进行排序。
因此gap的值的变化是一个从大到1的过程,可以用gap=gap/3+1来表示(gap初始值设置为该数组的元素个数),并且作为循环内部的表达式,这样一来gap的值就会不断的缩小至1,其中n表示数组的元素个数,+1的目的是保证让gap最小值为1,若不+1则会出现gap=0的情况,就会发生死循环了。
4、希尔排序的实现
在了解了希尔排序的逻辑以及gap的值对排序结果的影响后,用代码将其实现:
#include<stdio.h>
void ShellSort(int* a, int n)//希尔排序
{
int gap = n;//gap初始化为n,n表示数组内元素个数
while (gap > 1)
{
gap = gap / 3 + 1;//第一次循环先带着较大的gap去排序,后续gap的值慢慢变小,最后至1
for (int j = 0; j < gap; j++)//控制小数组
{
for (int i = j; i < n - gap; i+=gap)//将小数组内的元素进行排序
{
//插入排序思想
int end = i;
int temp = a[end + gap];//这里小数组内的元素间隔是gap,而不是1
while (end >= 0)
{
if (a[end] > temp)
{
a[end + gap] = a[end];
end -= gap;
}
else
break;
}
a[end + gap] = temp;
}
}
}
}
void PrintArr(int* a, int n)//打印数组
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
void Test_ShellSort()//希尔排序测试函数
{
int arr[] = { 9,8,7,6,5,4,3,2,1,0 };
int sz = sizeof(arr) / sizeof(int);
PrintArr(arr, sz);
ShellSort(arr, sz);
PrintArr(arr, sz);
}
int main()
{
Test_ShellSort();
return 0;
}运行结果:

三、插入排序与希尔排序性能对比测试
从代码的结构来看,会感觉到希尔排序的写法很复杂,而且逻辑也不简单,那么看起来如此复杂的希尔排序的性能一定比插入排序的性能要好吗,以下用一个测试代码进行对他们的性能测试:
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<time.h>
void ShellSort(int* a, int n)//希尔排序
{
int gap = n;//gap初始化为n,n表示数组内元素个数
while (gap > 1)
{
gap = gap / 3 + 1;//第一次循环先带着较大的gap去排序,后续gap的值慢慢变小,最后至1
for (int j = 0; j < gap; j++)//控制小数组
{
for (int i = j; i < n - gap; i += gap)//将小数组内的元素进行排序
{
//插入排序思想
int end = i;
int temp = a[end + gap];//这里小数组内的元素间隔是gap,而不是1
while (end >= 0)
{
if (a[end] > temp)
{
a[end + gap] = a[end];
end -= gap;
}
else
break;
}
a[end + gap] = temp;
}
}
}
}
void InsertSort(int* a, int n)//插入排序
{
for (int i = 0; i < n - 1; i++)
{
int end = i;//表示当前数组的最后一个元素的下标
int temp = a[i + 1];//一般而言,把end后一个元素看作是要插入进行排序的元素
//因此为了防止该元素被end的元素所覆盖,因此要先保存起来
while (end >= 0)//end小于0说明数组内元素都大于该插入的元素
{
if (a[end] > temp)//大于插入元素的情况
{
a[end + 1] = a[end];//“挪动”
end--;//遍历end
}
else//小于或等于插入元素的情况
break;//直接跳出
}
a[end + 1] = temp;//不论大于还是小于插入元素,都把要插入的元素给到end位置的后一位
}
}
//对比测试
void Contrast_test()
{
int n = 100000;
srand(time(0));
int* n1 = (int*)malloc(sizeof(int) * n);
int* n2 = (int*)malloc(sizeof(int) * n);
int* n3 = (int*)malloc(sizeof(int) * n);
int* n4 = (int*)malloc(sizeof(int) * n);
int* n5 = (int*)malloc(sizeof(int) * n);
for (int i = 0; i < n; i++)//构建一个100000个元素的数组,并且存放随机值
{
n1[i] = rand() % 10000;
n2[i] = n1[i];
n3[i] = n1[i];
n4[i] = n1[i];
n5[i] = n1[i];
}
//clock函数返回的是系统启动到调用该函数的时间,单位是毫秒,并存到变量中
int start1 = clock();
InsertSort(n1, n);
int end1 = clock();
int start2 = clock();
ShellSort(n2, n);
int end2 = clock();
printf("Test_InsertSort:%d\n", end1 - start1);//两个变量相减从而得到排序所消耗的时间
printf("Test_ShellSort:%d\n", end2 - start2);
free(n1);//释放空间
free(n2);
free(n3);
free(n4);
free(n5);
}
int main()
{
Contrast_test();
return 0;
}运行结果:

从结果可以观察到,插入排序的速度要比希尔排序的速度慢很多,也可以证明插入排序的消耗确实比希尔排序要大。
结语:
以上就是关于希尔排序的全部介绍以及实现,在掌握了希尔排序后会发现对插入排序的理解更加深刻了,其实各种不同的排序都有其存在的价值,也都有其适合的场景。最后希望本文可以给你带来更多的收获,如果本文对你起到了帮助,希望可以动动小指头帮忙点赞👍+关注😎+收藏👌!如果有遗漏或者有误的地方欢迎大家在评论区补充~!!谢谢大家!!
(~ ̄▽ ̄)~