专栏系列文章如下:
【视觉SLAM十四讲学习笔记】第一讲——SLAM介绍
【视觉SLAM十四讲学习笔记】第二讲——初识SLAM
【视觉SLAM十四讲学习笔记】第三讲——旋转矩阵
【视觉SLAM十四讲学习笔记】第三讲——Eigen库
【视觉SLAM十四讲学习笔记】第三讲——旋转向量和欧拉角
本章将介绍视觉SLAM的基本问题之一:如何描述刚体在三维空间中的运动?
四元数
四元数的定义
旋转矩阵用9个量描述3自由度的旋转,具有冗余性;欧拉角和旋转向量是紧凑的,但具有奇异性。事实上,我们找不到不带奇异性的三维向量描述方式。类似于用两个坐标表示地球表面(如经度和纬度),必定存在奇异性(纬度为 ±90° 时经度无意义)。回忆以前学习过的复数。我们用复数集C表示复平面上的向量,而复数的乘法则表示复平面上的旋转:乘上复数i相当于逆时针把一个复向量旋转 90°。类似地,在表达三维空间旋转时,也有一种类似于复数的代数:四元数(Quaternion)。四元数是Hamilton找到的一种扩展的复数。它既是紧凑的,也没有奇异性。缺点是四元数不够直观,其运算稍复杂些。
把四元数与复数类比可以更快地理解四元数。例如,当我们想要将复平面的向量旋转 θ 角时,可以给这个复向量乘以 e^iθ。这是极坐标表示的复数,它也可以写成普通的形式,只要使用欧拉公式即可:
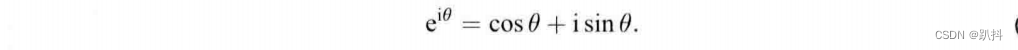
这是一个单位长度的复数。所以,在二维情况下,旋转可以由单位复数来描述。类似地,三维旋转则可以由单位四元数来描述。
一个四元数q拥有一个实部和三个虚部,示例如下:
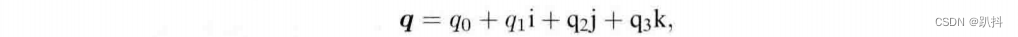
其中i,j,k为四元数的三个虚部。这三个虚部满足以下关系式:
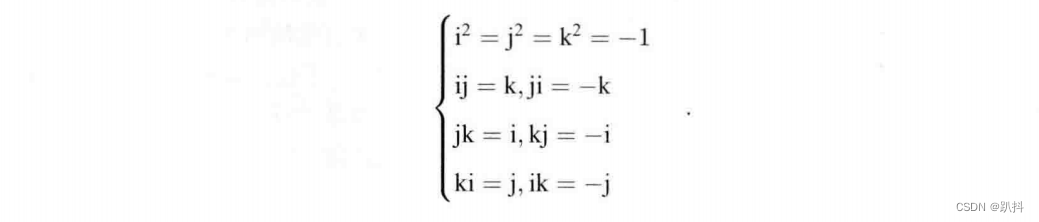
如果把i,j,k看成三个坐标轴,那么它们与自己的乘法和复数一样,相互之间的乘法和外积一样。有时人们也用一个标量和一个向量来表达四元数:
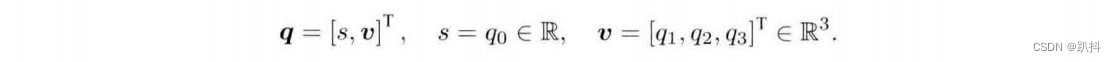
这里,s 称为四元数的实部,v称为它的虚部。如果一个四元数的虚部为0,称之为实四元数。反之,若它的实部为 0,则称之为虚四元数。
可以用单位四元数表示三维空间中任意一个旋转,不过这种表达方式和复数有些许不同。在复数中,乘以i意味着旋转 90°。这是否意味着四元数中,乘i就是绕i轴旋转90°?那么,ij=k是否意味着,先绕i转90°,再绕j转90°,就等于绕k转90°?
非也。应该是乘以i对应着旋转180◦,这样才能保证ij=k的性质。而i^2 = −1,意味着绕i轴旋转360°后得到一个相反的东西。这个东西要旋转两周(720°)才会和它原先的样子相等。(是不是很抽象)
四元数的运算
四元数常见的运算有四则运算、数乘、求逆、共轭等。
现在有两个四元数,原始表示为:
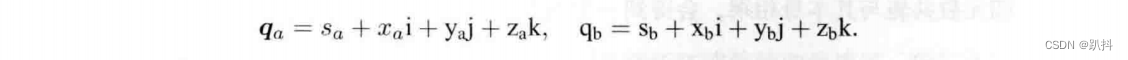
它们的向量表示为:
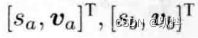
那么,其运算可表示如下:
-
加法和减法
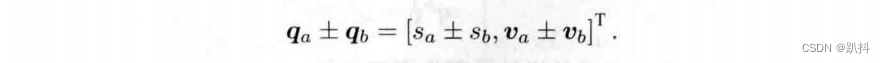
-
乘法
乘法是把qa的每一项和qb的每项相乘,最后相加:
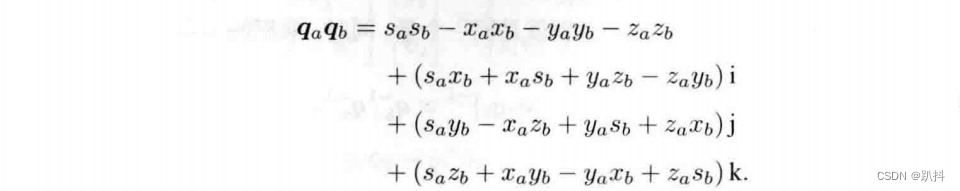
如果写成向量形式并利用内外积运算,该表达式会更加简洁:
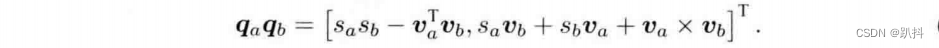
在该乘法定义下,两个实四元数乘积仍是实的,这与负数是一致的。然而我们注意到,由于最后一项外积的存在,四元数乘法通常是不可交换的,除非va和vb在R^3中共线,此时外积项为零。
-
模长
四元数的模长定义为
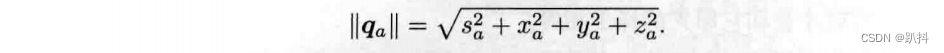
可以验证,两个四元数乘积的模即模的乘积。这使得单位四元数相乘后仍是单位四元数。
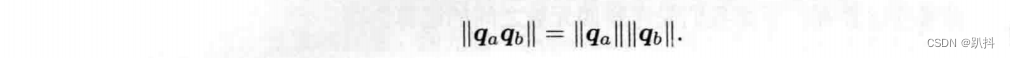
-
共轭
四元数的共轭是把虚部取成相反数:
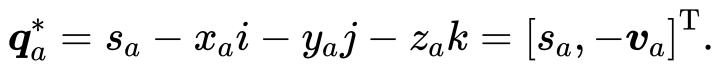
四元数共轭与其本身相乘,会得到一个实四元数,其实部为模长的平方:
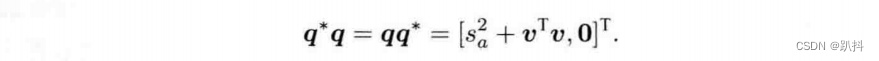
5. 逆
一个四元数的逆为
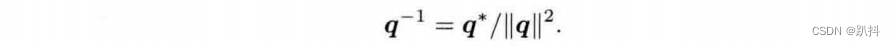
按此定义,四元数和自己的逆的乘积为实四元数1:
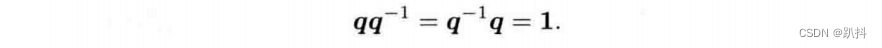
如果q为单位四元数,其逆和共轭就是同一个量。同时,乘积的逆具有和矩阵相似的性质:
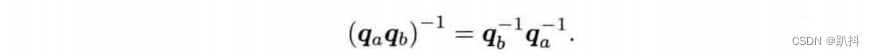
-
数乘
和向量相似,四元数可以与数相乘:
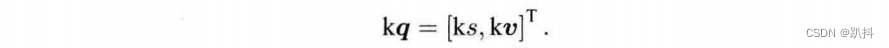
用四元数表示旋转
我们可以用四元数表达对一个点的旋转。假设有一个空间三维点
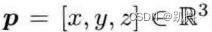
以及一个由单位四元数q指定的旋转。三维点p经过旋转之后变为p‘。如果使用矩阵描述,那么有p’=Rp。而如果用四元数描述旋转,它们的关系又如何表达呢?
首先,把三位空间点用一个虚四元数来描述:
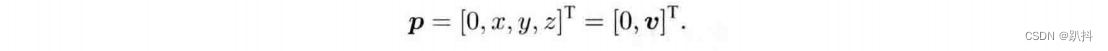
相当于把四元数的3个虚部与空间中的3个轴相对应。那么,旋转后的点p‘可表示为这样的乘积:
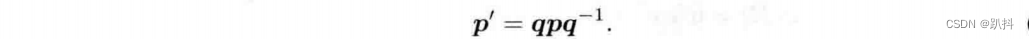
这里的乘法均为四元数乘法,结果也是四元数。最后把p’的虚部取出,即得旋转之后点的坐标。并且,计算结果的实部为0,故为纯虚四元数。
四元数到其他旋转表示的转换
任意单位四元数描述了一个旋转,该旋转也可用旋转矩阵或旋转向量描述。四元数乘法也可以写成一种矩阵的乘法。设q = [s,v]^T,那么,定义如下的符号 + 和 ⊕ 为:
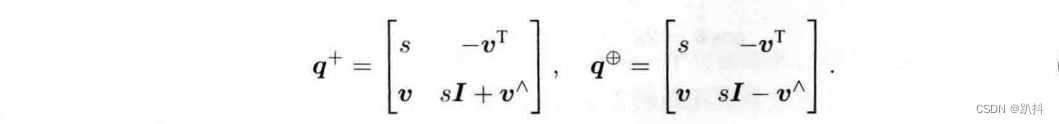
这两个符号将四元数映射成为一个 4×4 的矩阵。于是四元数乘法可以写成矩阵的形式:

同理亦可证:
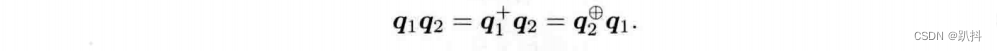
然后,考虑使用四元数对空间点进行旋转的问题:
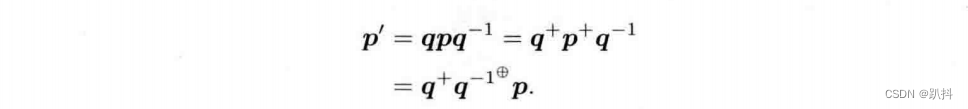
代入两个符号对应的矩阵,得:
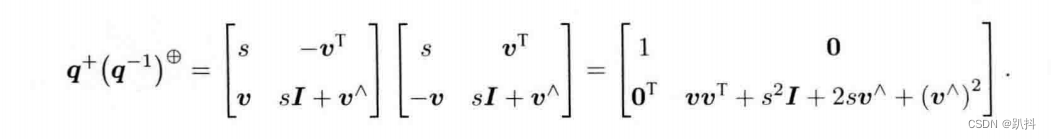
因为p′和p都是虚四元数,那么事实上该矩阵的右下角即给出了从四元数到旋转矩阵的变换关系:
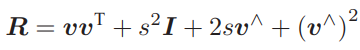
对上式两侧求迹,得:
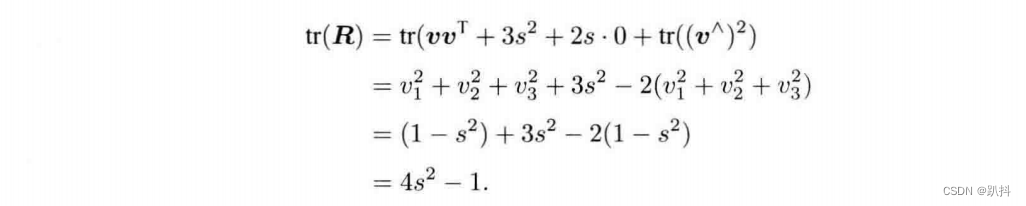
又由
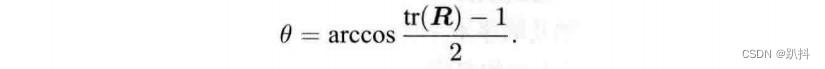
得到
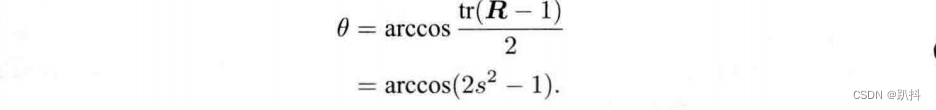
即
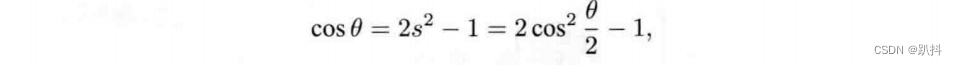
所以
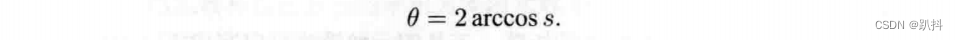
总而言之,四元数到旋转向量的转换公式如下:
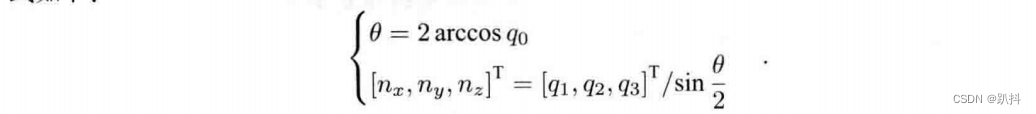
…(img-gkaQjiLn-1701177419079)]
代入两个符号对应的矩阵,得:
[外链图片转存中…(img-vQsuOEIL-1701177419080)]
因为p′和p都是虚四元数,那么事实上该矩阵的右下角即给出了从四元数到旋转矩阵的变换关系:
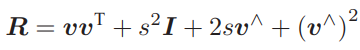









![[学习记录]Node event loop 总结流程图](https://img-blog.csdnimg.cn/direct/b78dc1b528454696aebc0eece4c9fb3e.jpeg#pic_center)