目录
- 问题描述
- 递推关系
- 建立递推关系的思路
- 约束条件:以 s [ k ] s[k] s[k] 结尾
- 约束条件:以 s [ k ] s[k] s[k] 开头
- 约束条件:增加子问题参数(前缀)
- 约束条件:增加子问题参数(后缀)
- 约束条件:LIS长度为k且末尾元素最小
- 运行实例
问题描述
最长递增子序列(Longest Increasing Subsequence,
LIS)
- 子序列:对于任意序列s,它的子序列是通过删除其中零个或多个元素得到的另⼀个序列
注:剩余元素的相对顺序保持不变给定n个整数组成的序列 s [ 1... n ] s[1...n] s[1...n],求最长递增子序列LIS(的长度)
| 8 | 3 | 6 | 1 | 3 | 5 | 4 | 7 |
|---|
递推关系
建立递推关系的思路
假设能够求出
s
[
1...
k
−
1
]
s[1...k-1]
s[1...k−1] 的 LIS,考虑能否由此推出
s
[
1...
k
]
s[1...k]
s[1...k] 的 LIS
- 如果仅知道长度
- 无法判断
s
[
k
]
s[k]
s[k] 能否让
LIS变长
- 无法判断
s
[
k
]
s[k]
s[k] 能否让
- 如果不仅知道长度,还知道具体序列 L
- s [ k ] s[k] s[k] 能让 L 变长,那问题就解决了
- 也许 L 就是
s
[
1...
k
]
s[1...k]
s[1...k] 的
LIS - 也许存在
s
[
1...
k
]
s[1...k]
s[1...k] 的另⼀个
LIS:L‘, s [ k ] s[k] s[k] 能让L’变长 - 可能需要记住
s
[
1...
k
−
1
]
s[1...k-1]
s[1...k−1] 的所有
LIS
原始子问题: 令
L
(
k
)
L(k)
L(k) 表示
s
[
1...
k
]
s[1...k]
s[1...k] 的LIS的长度,原问题即求解
L
(
n
)
L(n)
L(n)
- O(n)个子问题,但不容易建立递归关系
约束条件:以 s [ k ] s[k] s[k] 结尾
- 令
L
(
k
)
L(k)
L(k) 表示
s
[
1...
n
]
s[1...n]
s[1...n] 中以
s
[
k
]
s[k]
s[k] 结尾的
LIS的长度 - 原问题即为求解 max 1 ≤ k ≤ n L ( k ) \max_{1\le k\le n}L(k) max1≤k≤nL(k)
- 基本情况: 如果 k = 1 k = 1 k=1,那么 L ( k ) = 1 L(k) = 1 L(k)=1
- 归纳步骤
- L k = max { 1 , max 1 ≤ i ≤ k − 1 { L ( i ) + 1 ∣ s [ k ] > s [ i ] } } L_k = \max \{1, \max_{1\le i \le k-1} \{ L(i) +1 | s[k] > s[i] \}\} Lk=max{1,max1≤i≤k−1{L(i)+1∣s[k]>s[i]}},其中, max ⊘ \max \oslash max⊘的值定义为0

- 此时的递推关系:
L ( k ) = { 1 i f k = 1 max { 1 , max 1 ≤ i ≤ k − 1 { L ( i ) + 1 ∣ s [ k ] > s [ i ] } } i f k > 1 L(k) = \begin{cases} 1 &if\quad k=1\\ \max \{1, \max_{1\le i \le k-1} \{ L(i) +1 | s[k] > s[i] \}\} &if \quad k>1 \end{cases} L(k)={1max{1,max1≤i≤k−1{L(i)+1∣s[k]>s[i]}}ifk=1ifk>1
- O ( n ) O(n) O(n) 个子问题,每个子问题复杂度为 O ( k ) O(k) O(k)。时间复杂度为 O ( n 2 ) O(n^2) O(n2)
约束条件:以 s [ k ] s[k] s[k] 开头
- 令
L
(
k
)
L(k)
L(k) 表示
s
[
1...
n
]
s[1...n]
s[1...n] 中以
s
[
k
]
s[k]
s[k] 开头的
LIS的长度 - 原问题即为求解 max 1 ≤ k ≤ n L ( k ) \max_{1\le k\le n}L(k) max1≤k≤nL(k)
- 基本情况: 如果 k = n k = n k=n,那么 L ( k ) = 1 L(k) = 1 L(k)=1

- 此时的递推关系:
L ( k ) = { 1 i f k = n max { 1 , max k + 1 ≤ i ≤ n { L ( i ) + 1 ∣ s [ k ] < s [ i ] } } i f k < n L(k) = \begin{cases} 1 &if\quad k=n\\ \max \{1, \max_{k+1\le i \le n} \{ L(i) +1 | s[k] < s[i] \}\} &if \quad k<n \end{cases} L(k)={1max{1,maxk+1≤i≤n{L(i)+1∣s[k]<s[i]}}ifk=nifk<n
- O ( n ) O(n) O(n) 个子问题,每个子问题复杂度为 O ( k ) O(k) O(k)。时间复杂度为 O ( n 2 ) O(n^2) O(n2)
约束条件:增加子问题参数(前缀)
- 令
L
(
i
,
j
)
L(i,j)
L(i,j) 表示
s
[
j
.
.
.
n
]
s[j...n]
s[j...n] 中每个元素都大于
s
[
i
]
s[i]
s[i] 的
LIS的长度 - 令 s [ 0 ] = − ∞ s[0] =-\infty s[0]=−∞ ,原问题即求解 L ( 0 , 1 ) L(0,1) L(0,1)
- 基本情况: 如果 j > n j> n j>n ,那么 L ( i , j ) = 0 L(i,j)= 0 L(i,j)=0

- 归纳步骤
- 如果 s [ i ] > s [ j ] s[i] > s[j] s[i]>s[j], L ( i , j ) = L ( i , j + 1 ) L(i,j) = L(i,j+ 1) L(i,j)=L(i,j+1)
- 否则 L ( i , j ) = max { L ( i , j + 1 ) , 1 + L ( j , j + 1 ) } L(i,j) = \max \{ L(i,j+ 1),1 + L(j,j+ 1)\} L(i,j)=max{L(i,j+1),1+L(j,j+1)}
- O ( n 2 ) O(n^2) O(n2)个子问题,每个子问题求解复杂度为 O ( 1 ) O(1) O(1),时间复杂度: O(n2); 空间复杂度: O(n2)
- 此时的递推关系:
L ( i , j ) = { 0 i f j > n L ( i , j + 1 ) i f s [ i ] ≥ s [ j ] max { L ( i , j + 1 ) 1 + L ( j , j + 1 ) o t h e r w i s e L(i,j) = \begin{cases} 0 &if\quad j>n\\ L(i,j+1) &if\quad s[i]\ge s[j] \\ \max \begin{cases} L(i,j+1) \\ 1+L(j,j+1) \end{cases} &otherwise \end{cases} L(i,j)=⎩ ⎨ ⎧0L(i,j+1)max{L(i,j+1)1+L(j,j+1)ifj>nifs[i]≥s[j]otherwise

约束条件:增加子问题参数(后缀)
- 令
L
(
i
,
j
)
L(i,j)
L(i,j) 表示
s
[
1...
j
]
s[1...j]
s[1...j] 中每个元素都小于
s
[
i
]
s[i]
s[i] 的
LIS的长度 - 令 s [ n + 1 ] = ∞ s[n+1] =\infty s[n+1]=∞ ,原问题即求解 L ( n + 1 , n ) L(n+1,n) L(n+1,n)
- 基本情况: 如果 j = 0 j=0 j=0 ,那么 L ( i , j ) = 0 L(i,j)= 0 L(i,j)=0

-
归纳步骤
- 如果 s [ i ] ≤ s [ j ] s[i] \le s[j] s[i]≤s[j], L ( i , j ) = L ( i , j − 1 ) L(i,j) = L(i,j- 1) L(i,j)=L(i,j−1)
- 否则 L ( i , j ) = max { L ( i , j − 1 ) , 1 + L ( j , j − 1 ) } L(i,j) = \max \{ L(i,j- 1),1 + L(j,j- 1)\} L(i,j)=max{L(i,j−1),1+L(j,j−1)}
-
此时的递推关系:
L ( i , j ) = { 0 i f j = 0 L ( i , j − 1 ) i f s [ i ] ≤ s [ j ] max { L ( i , j − 1 ) 1 + L ( j , j − 1 ) o t h e r w i s e L(i,j) = \begin{cases} 0 &if\quad j=0\\ L(i,j-1) &if\quad s[i]\le s[j] \\ \max \begin{cases} L(i,j-1) \\ 1+L(j,j-1) \end{cases} &otherwise \end{cases} L(i,j)=⎩ ⎨ ⎧0L(i,j−1)max{L(i,j−1)1+L(j,j−1)ifj=0ifs[i]≤s[j]otherwise

约束条件:LIS长度为k且末尾元素最小
-
对于长度为 k k k 的递增子序列,只需记住末尾元素最小的那个
-
本质是寻找上限最高(可拓展性最强)的那个子序列
-
令 L ( k ) L(k) L(k) 表示 s [ 1... n ] s[1...n] s[1...n] 中长度为 k k k 且末尾元素最小的递增子序列,且 L ( k ) . l a s t L(k).last L(k).last 表示该序列中最后那个元素
-
引理: L ( 1 ) . l a s t < L ( 2 ) . l a s t < . . . < L ( k ) . l a s t L(1) .last < L(2) .last < ... < L(k).last L(1).last<L(2).last<...<L(k).last
- 假设 x ≥ y x \ge y x≥y,而 y ≥ z y \ge z y≥z,所以 x ≥ z x \ge z x≥z
- 那么灰色元素构成一个长度为
k
k
k 且末尾元素最小的递增子序列,矛盾

-
归纳假设: 对长度小于 n n n 的序列,可以计算其所有的 L ( k ) L(k) L(k),并有序存储
-
基本情况: 长度为1的序列,有 L [ 1 ] ← s [ 1 ] L[1]\leftarrow s[1] L[1]←s[1]
-
如何基于归纳假设求解 s [ 1.. n ] s[1..n] s[1..n] 的所有的 L ( k ) L(k) L(k)
- 在 L ( k ) . l a s t L(k).last L(k).last 构成的有序数组中查找插入位置 k ′ k' k′,使得 s [ n ] s[n] s[n] 加入后仍然有序
- 如果 k ′ = k + 1 k' =k+1 k′=k+1,那么 L ( k + 1 ) + L ( k ) + 1 L(k + 1) + L(k) +1 L(k+1)+L(k)+1 且 L ( k + 1 ) . l a s t ← s [ n ] L(k + 1).last \leftarrow s[n] L(k+1).last←s[n]
- 否则 L ( k ′ ) . l a s t ← s [ n ] L(k').last \leftarrow s[n] L(k′).last←s[n],但 L ( k ′ ) L(k') L(k′) 的值不变
-
时间复杂度: O ( l o g n ) O(logn) O(logn)

运行实例
#include <iostream>
#include <vector>
#include <algorithm>
#include <set>
using namespace std;
ostream& operator<<(ostream& os, const vector<int>& v) {
for (auto e : v)
os << e << ' ';
return os;
}
int lis_dp1(const vector<int>& s, int n) {
vector<int> dp(n + 1, 1); // 初始化dp数组,dp[i]表示以s[i]结尾的LIS的长度
for (int k = 2; k <= n; ++k) {
for (int i = 1; i < k; ++i) {
if (s[k] > s[i]) {
dp[k] = max(dp[k], dp[i] + 1);
}
}
}
return *max_element(dp.begin(), dp.end()); // 返回dp数组中的最大值作为整个序列的最长递增子序列的长度
}
int lis_dp2(const vector<int>& s, int n) {
vector<vector<int>> dp(n + 2, vector<int>(n + 2, -1)); // 初始化dp数组,dp[i][j]表示L(i,j)
for (int i = 0; i <= n + 1; ++i)
dp[i][n + 1] = 0; // 基本情况:当 j > n 时,L(i,j) = 0
for (int j = n; j >= 1; --j) {
for (int i = 0; i < j; ++i) {
if (s[i] >= s[j]) {
dp[i][j] = dp[i][j + 1]; // 如果s[i] >= s[j],则L(i,j) = L(i,j+1)
}
else {
dp[i][j] = max(dp[i][j + 1], 1 + dp[j][j + 1]); // 否则L(i,j) = max{L(i,j+1), 1+L(j,j+1)}
}
}
}
return dp[0][1]; // 返回L(0,1)作为整个序列的最长递增子序列的长度
}
int lis_dp3(const vector<int>& s, int n) {
if (n == 0) return 0;
set<int> L;
L.insert(s[1]);
for (int i = 2; i < n+1; ++i) {
if (s[i] > * L.rbegin()) {
L.insert(s[i]);
}
else {
L.erase(L.lower_bound(s[i]));
L.insert(s[i]);
}
}
return L.size();
}
vector<int> find_lis_dp1(const vector<int>& s, int n) {
vector<int> dp(n + 1, 1); // 初始化dp数组,dp[i]表示以s[i]结尾的LIS的长度
vector<int> parent(n + 1, -1); // 记录每个元素的父节点索引
for (int k = 2; k <= n; ++k) {
for (int i = 1; i < k; ++i) {
if (s[k] > s[i] && dp[k] < dp[i] + 1) {
dp[k] = dp[i] + 1;
parent[k] = i; // 更新父节点索引
}
}
}
int max_length = *max_element(dp.begin(), dp.end()); // 获取最长递增子序列的长度
int max_index = distance(dp.begin(), find(dp.begin(), dp.end(), max_length)); // 获取最长递增子序列的结束索引
vector<int> lis;
while (max_index != -1) {
lis.push_back(s[max_index]);
max_index = parent[max_index]; // 根据父节点索引回溯
}
reverse(lis.begin(), lis.end()); // 反转得到正确顺序的最长递增子序列
return lis;
}
vector<int> find_lis_dp2(const vector<int>& s, int n) {
vector<vector<int>> dp(n + 2, vector<int>(n + 2, -1)); // 初始化dp数组,dp[i][j]表示L(i,j)
vector<vector<int>> parent(n + 2, vector<int>(n + 2, -1)); // 记录每个元素的父节点索引
for (int i = 0; i <= n + 1; ++i)
dp[i][n + 1] = 0; // 基本情况:当 j > n 时,L(i,j) = 0
for (int j = n; j >= 1; --j) {
for (int i = 0; i < j; ++i) {
if (s[i] >= s[j]) {
dp[i][j] = dp[i][j + 1];
}
else {
dp[i][j] = max(dp[i][j + 1], 1 + dp[j][j + 1]);
if (dp[i][j] == dp[j][j + 1] + 1) {
parent[i][j] = j; // 更新父节点索引
}
}
}
}
vector<int> lis;
int i = 0, j = 1;
while (j <= n) {
if (dp[i][j] == dp[j][j + 1] + 1) {
lis.push_back(s[j]);
i = j;
}
++j;
}
return lis;
}
vector<int> find_lis_dp3(const vector<int>& s, int n) {
vector<int> lis;
set<int> L;
L.insert(s[1]);
for (int i = 2; i < n + 1; ++i) {
if (s[i] > *L.rbegin()) {
L.insert(s[i]);
}
else {
L.erase(L.lower_bound(s[i]));
L.insert(s[i]);
}
}
for (int num : L) {
lis.push_back(num);
}
return lis;
}
int main(int argc, const char* argv[]) {
vector<int> s = { -1, 8, 3, 6, 1, 3, 5, 4, 7 }; // 注意s[0]仅作标识,真实数据为s[1]~s[n]
cout << lis_dp1(s, s.size() - 1) << endl;
cout << find_lis_dp1(s, s.size() - 1) << endl;
cout << "------------------------------" << endl;
cout << lis_dp2(s, s.size() - 1) << endl;
cout << find_lis_dp2(s, s.size() - 1) << endl;
cout << "------------------------------" << endl;
cout << lis_dp3(s, s.size() - 1) << endl;
cout << find_lis_dp3(s, s.size() - 1) << endl;
cout << "------------------------------" << endl;
return 0;
}
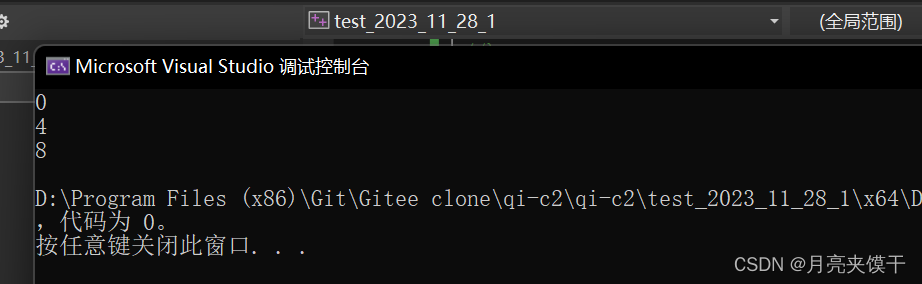
运行结果: