双指针算法可以帮忙把时间复杂度降低一个维度,即原本O(n2)降为O(n);将O(n)降为O(1)
移动零
移动零
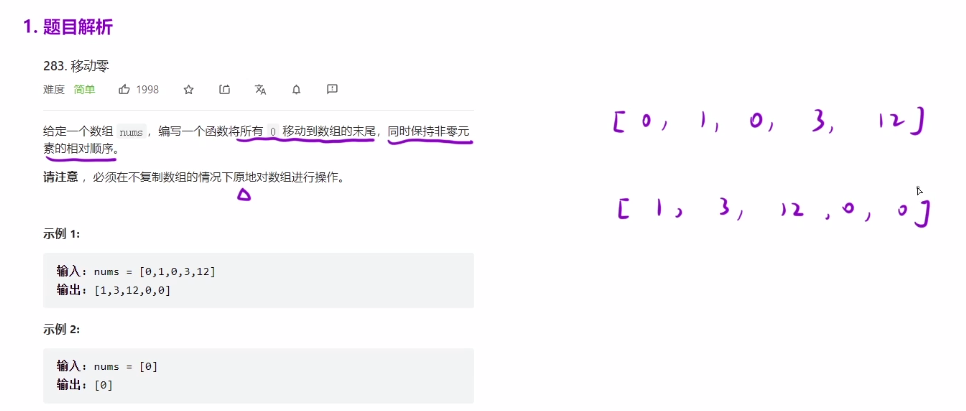
题目解析
- 将所有0移动到末尾
- 保持非0元素相对顺序
- 对数组进行原地操作(不开辟额外空间)
算法原理
数组划分/数组分块——划分为非0元素和0元素两个区间
解决方法:双指针算法(利用数组下标充当指针)
原理: ⽤⼀个 cur 指针来扫描整个数组,另⼀个 dest 指针⽤来记录⾮零数序列 的最后⼀个位置。根据 cur 在扫描的过程中,遇到的不同情况,分类处理,实现数组的划分。 在 cur 遍历期间,使 [0, dest] 的元素全部都是⾮零元素, [dest + 1, cur - 1] 的 元素全是零。
流程:
-
** **a. 初始化 cur = 0 (⽤来遍历数组), dest = -1 (指向⾮零元素序列的最后⼀个位置。 因为刚开始我们不知道最后⼀个⾮零元素在什么位置,因此初始化为 -1 )
-
b. cur 依次往后遍历每个元素,遍历到的元素会有下⾯两种情况:
i. 遇到的元素是 0 , cur 直接 ++ 。因为我们的⽬标是让 [dest + 1, cur - 1] 内 的元素全都是零,因此当 cur 遇到 0 的时候,直接 ++ ,就可以让 0 在 cur - 1 的位置上,从⽽在 [dest + 1, cur - 1] 内; <br />ii. 遇到的元素不是 0 , dest++ ,并且交换 cur 位置和 dest 位置的元素,之后让 cur++ ,扫描下⼀个元素。<br /> • 因为 dest 指向的位置是⾮零元素区间的最后⼀个位置,如果扫描到⼀个新的⾮零元 素,那么它的位置应该在 dest + 1 的位置上,因此 dest 先⾃增 1 ; <br />• dest++ 之后,指向的元素就是 0 元素(因为⾮零元素区间末尾的后⼀个元素就是 0 ),因此可以交换到 cur 所处的位置上,实现 [0, dest] 的元素全部都是⾮零 元素, [dest + 1, cur - 1] 的元素全是零。 <br />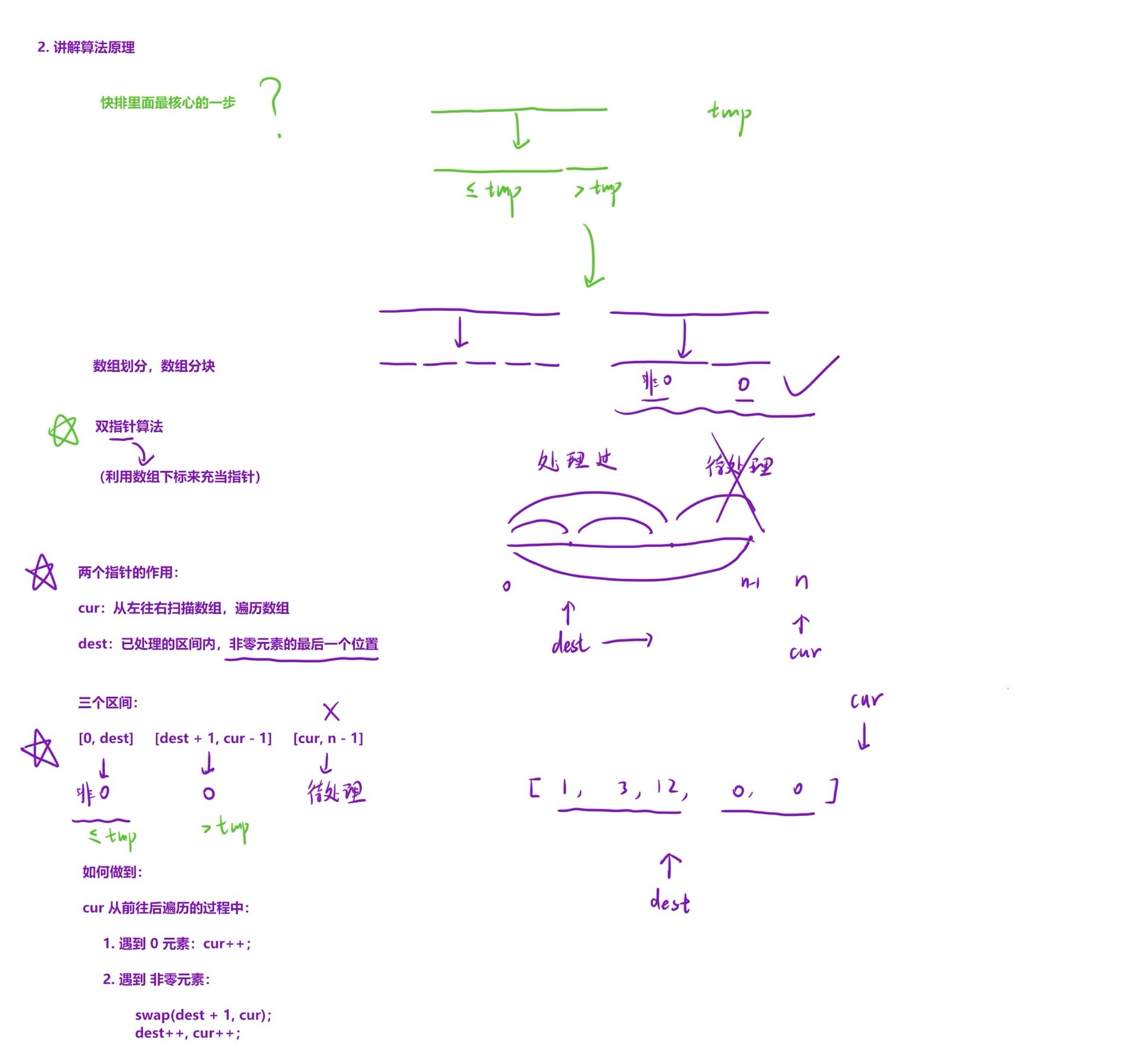
代码实现
class Solution {
public:
void moveZeroes(vector<int>& nums) {
for (int cur = 0, dest = -1; cur < nums.size(); cur++)
{
if(nums[cur]) //处理非0元素
swap(nums[++dest],nums[cur]);
}
}
};
复写零
复写零
题目解析
- 不要超过数组长度
- 不要开辟额外空间
算法原理
解法:依旧是双指针算法
思路:先根据"异地"操作,然后优化成双指针下的"就地"操作
流程:
- 先找到最后一个复写的数
- 处理边界情况(eg:1,0,2,3,0,4这样dest最终会造成越界访问)
- 从后向前完成复写操作
注意:这里不能从前向后进行复写,否则会覆盖掉后面的数字
a. 初始化两个指针 cur = 0 , dest = 0 ;
b. 找到最后⼀个复写的数:
i. 当cur < n 的时候,⼀直执⾏下⾯循环:
• 判断 cur 位置的元素:
◦ 如果是 0 的话, dest 往后移动两位;
◦ 否则, dest 往后移动⼀位。
• 判断dest 时候已经到结束位置,如果结束就终⽌循环;
• 如果没有结束, cur++ ,继续判断。
c. 判断 dest 是否越界到 n 的位置:
i. 如果越界,执⾏下⾯三步:
- n - 1 位置的值修改成 0 ;
- cur 向移动⼀步;
- dest 向前移动两步。
d. 从cur 位置开始往前遍历原数组,依次还原出复写后的结果数组:
i. 判断cur 位置的值:
- 如果是 0 : dest 以及 dest - 1 位置修改成 0 , dest -= 2 ;
- 如果⾮零: dest 位置修改成 0 , dest -= 1 ;
ii. cur-- ,复写下⼀个位置
代码实现
class Solution {
public:
void duplicateZeros(vector<int>& arr) {
//1.先找到最后一个数
int cur = 0;
int dest = -1;
while(cur<arr.size())
{
if(arr[cur])
dest++;
else
dest += 2;
if(dest >= arr.size()-1) break;
cur++;
}
//2.处理边界情况
if(dest==arr.size())
{
arr[arr.size()-1] = 0;
cur--;
dest -= 2;
}
//3.从后向前复写
while(cur >= 0)
{
if(arr[cur])
arr[dest--] = arr[cur--];
else
{
arr[dest--] = 0;
arr[dest--] = 0;
cur--;
}
}
}
};
快乐数
快乐数
题目解析
- 题目定义快乐数的第一种情况:这个数会变成1,是快乐数
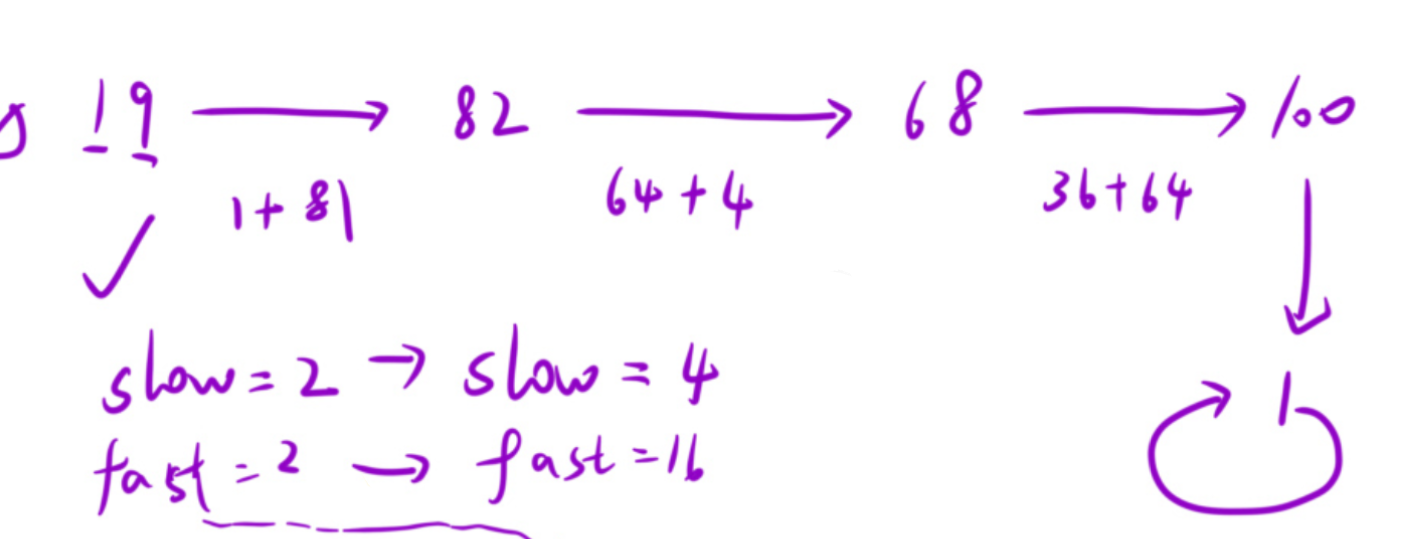
- 题目定义快乐数的第二种情况:会陷入某一个环里开始循环,永远变不为1所以不是快乐数
算法原理
- 第一种情况相当于也是一个环,只不过环中所有的数都是1
- 第二种情况所有环中的数都不是1
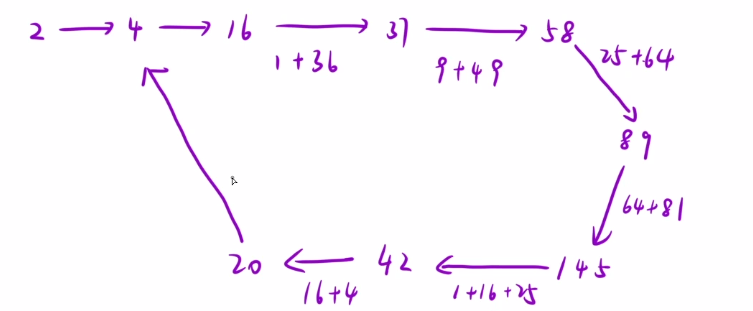
所以以上两种情况抽象成一种,即总会进入一个环里开始循环。故只需要判断链表里是否有1就能确定是否有快乐数。(ps:类似判断列表是否有环——快慢指针)
快慢指针:慢指针每次向后移动一步,快指针每次向后移动两步;判断相遇时候的值即可
题目中告诉我们最终出现的两种情况——1.变成1一直循环下去 2.在循环里永远变不为1。若题目不给出这句话,我们也可以证明出来
鸽巢原理(抽屉原理)
n个鸽巢,n+1只鸽子——至少会有一个巢穴有大于1的鸽子数
题目中数据范围时int的最大值231-1(2.1*109) 让这个数再大一点,方便我们确定范围
因为最大的数只能到810,每次变化时都会落在[1,810]这个区间里,所以当我们变化次数超过810时,他一定会有重复的数字落入这个范围里,即一定会进入环里。
代码实现
class Solution {
public:
// 返回 n 这个数每⼀位上的平⽅和
int bitSum(int n)
{
int sum = 0;
while(n)
{
int t = n % 10;
sum += t * t;
n /= 10;
}
return sum;
}
bool isHappy(int n)
{
int slow = n, fast = bitSum(n);
while(slow != fast)
{
slow = bitSum(slow);
fast = bitSum(bitSum(fast));
}
return slow == 1;
}
};
盛水最多的容器
盛水最多的容器
题目解析
选两条线,取较小的(木桶原理)与x轴进行相乘算出容积
算法原理
-
暴力枚举:先固定最左边的线,依次乘,把所有情况全算出来找出最大值(两层for循环)时间复杂度O(n^2)

-
利用单调性,使用双指针,即对撞指针(时间复杂度O(n),空间复杂度O(1))
-
先寻找规律:即随便取两个数,研究一个小区间,然后拿两个中较小的数向内枚举。如图可以看出,要么h会减小,要么w宽度会减小,所以直接把4这个数字pass掉,不需要进行枚举。
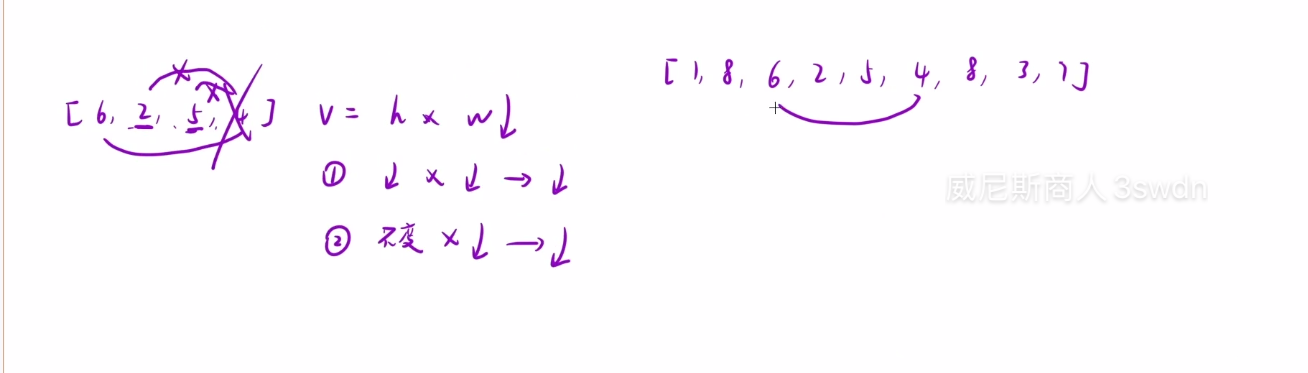
-
扩大规律,直接拿最左边的数和最右边的数,计算出V1,然后向内枚举时可以舍弃掉1(较小的数),研究下一段区间。当两个指针相遇时,我们计算出所有的V取最大值即可。
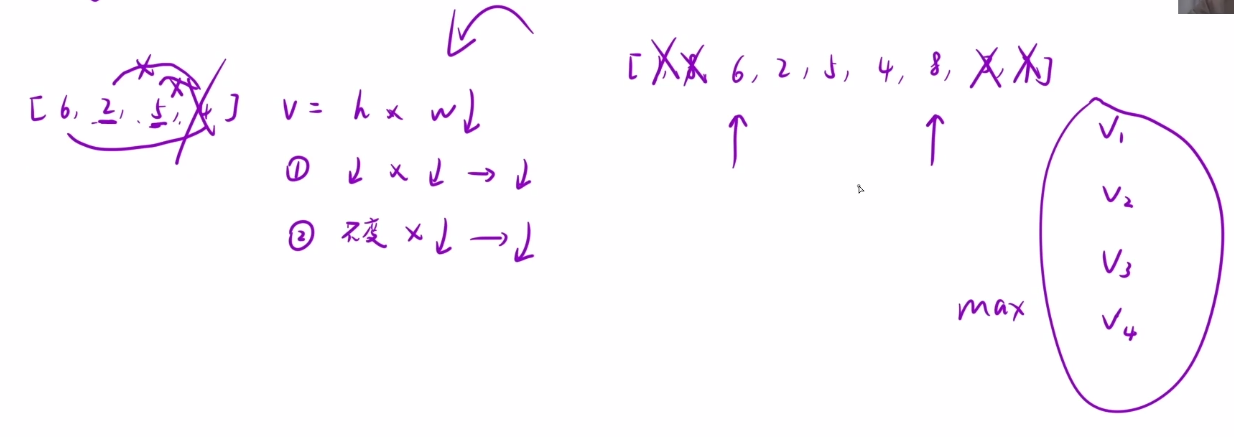
代码实现
class Solution {
public:
int maxArea(vector<int>& height)
{
int left = 0, right = height.size() - 1, ret = 0;
while(left < right)
{
int v = min(height[left], height[right]) * (right - left);
ret = max(ret, v);
// 移动指针
if(height[left] < height[right])
left++;
else
right--;
}
return ret;
}
};
有效三角形个数
有效三角形个数
题目解析
emm三角形两边之和大于第三边(hhhh)
算法原理
- 暴力枚举——令a+b>c a+c>b b+c>a三个条件同时成立即可,但这个方法要判断三次
判断三⻆形的优化:
- 如果能构成三⻆形,需要满⾜任意两边之和要⼤于第三边。但是实际上只需让较⼩的两条边之和⼤于第三边即可。
- 因此我们可以先将原数组排序,然后从⼩到⼤枚举三元组,⼀⽅⾯省去枚举的数量,另⼀⽅⾯⽅便判断是否能构成三⻆形
//超时
class Solution {
public:
int triangleNumber(vector<int>& nums) {
// 1. 排序
sort(nums.begin(), nums.end());
int n = nums.size(), ret = 0;
// 2. 从⼩到⼤枚举所有的三元组
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
for (int k = j + 1; k < n; k++) {
// 当最⼩的两个边之和⼤于第三边的时候,统计答案
if (nums[i] + nums[j] > nums[k])
ret++;
}
}
}
return ret;
}
};
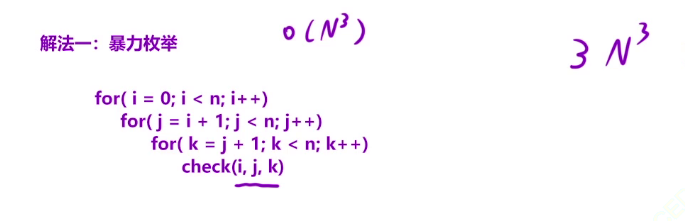
- 单调性,双指针
先将数组排序。根据「解法⼀」中的优化思想,我们可以固定⼀个「最⻓边」,然后在⽐这条边⼩的有序数组中找出⼀个⼆元组,使这个⼆元组之和⼤于这个最⻓边。由于数组是有序的,我们可以利⽤「对撞指针」来优化。
设最⻓边枚举到 i 位置,区间[left, right] 是 i 位置左边的区间(也就是⽐它⼩的区间):
- 如果 nums[left] + nums[right] > nums[i] :
- 说明 [left, right - 1] 区间上的所有元素均可以与 nums[right] 构成⽐nums[i] ⼤的⼆元组
- 满⾜条件的有 right - left 种情况(下标相减)
- 此时 right 位置的元素的所有情况相当于全部考虑完毕, right-- ,进⼊下⼀轮判断
- 如果 nums[left] + nums[right] <= nums[i] :
- 说明 left 位置的元素是不可能与 [left + 1, right] 位置上的元素构成满⾜条件的⼆元组
- left 位置的元素可以舍去, left++ 进⼊下轮循环 (即换一个固定的数,重复上述过程)

代码实现
class Solution {
public:
int triangleNumber(vector<int>& nums)
{
// 1. 优化
sort(nums.begin(), nums.end());
// 2. 利⽤双指针解决问题
int ret = 0, n = nums.size();
for(int i = n - 1; i >= 2; i--) // 先固定最⼤的数
{
// 利⽤双指针快速统计符合要求的三元组的个数
int left = 0, right = i - 1;
while(left < right)
{
if(nums[left] + nums[right] > nums[i])
{
ret += right - left;
right--;
}
else
{
left++;
}
}
}
return ret;
}
};
和为s的两个数字
和为s的两个数字
题目解析
- 数组是有序的
- 最终结果返回数字,如果有多对,只需返回一对即可
算法原理
- 暴力解法
仅需两个for循环,先固定一个数,挨个相加。但没有利用数组有序的特性。
- 双指针算法——对撞指针
- 当left+right > target;那么right所指的数舍去,right–
- 当left+right < target;那么[left+1,right] 之间的数都不可能满足,所以left++
- 当left+right = target; 返回
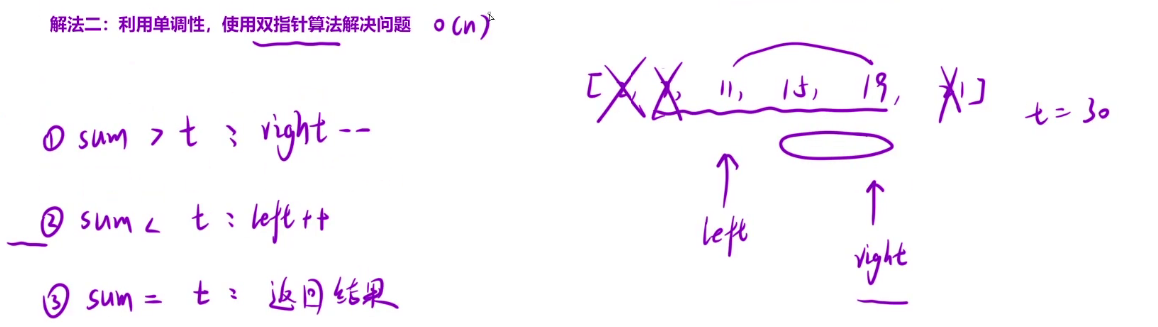
代码实现
class Solution {
public:
vector<int> twoSum(vector<int>& price, int target) {
int left = 0,right = price.size()-1;
while(left < right)
{
int sum = price[left] + price[right];
if (sum < target) left++;
else if(sum > target) right--;
else return{price[left],price[right]}; //C++语法,初始化列表(隐形转换,会自动转换成vector<int>)
}
//照顾编译器,让所有路径有返回值
return{-4221,-1};
}
};
//当返回值是vector,并且只需要返回两个变量时,可以用初始化列表写法
三数之和
三数之和
题目解析
- 要求选三个不同位置的数
- 注意中的不允许重复是指即使三个数位置不同,也都满足结果,但因为元素一样,所以只选择一组即可
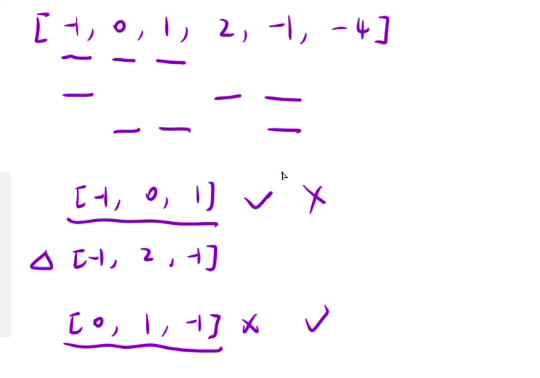
算法原理
- 解法一:排序+暴力枚举+set去重
去重操作我们是使用容器进行,是常数级别,可以忽略不计,在面试时,往往要求我们不使用现成的容器进行去重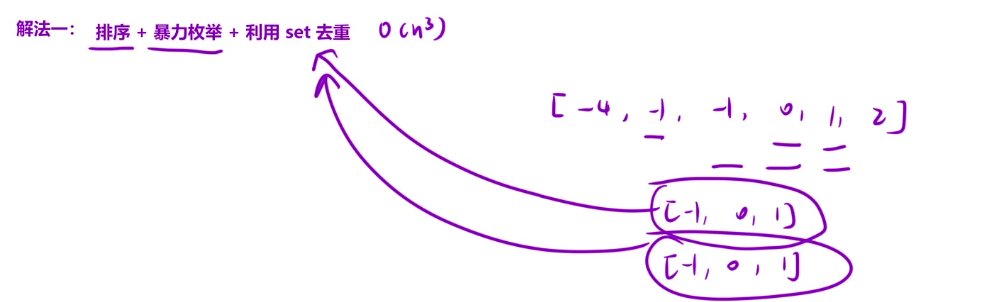
- 解法二:排序+双指针
(有点类似上道题的两数之和) 这里去重我们尝试不使用容器set
注意:
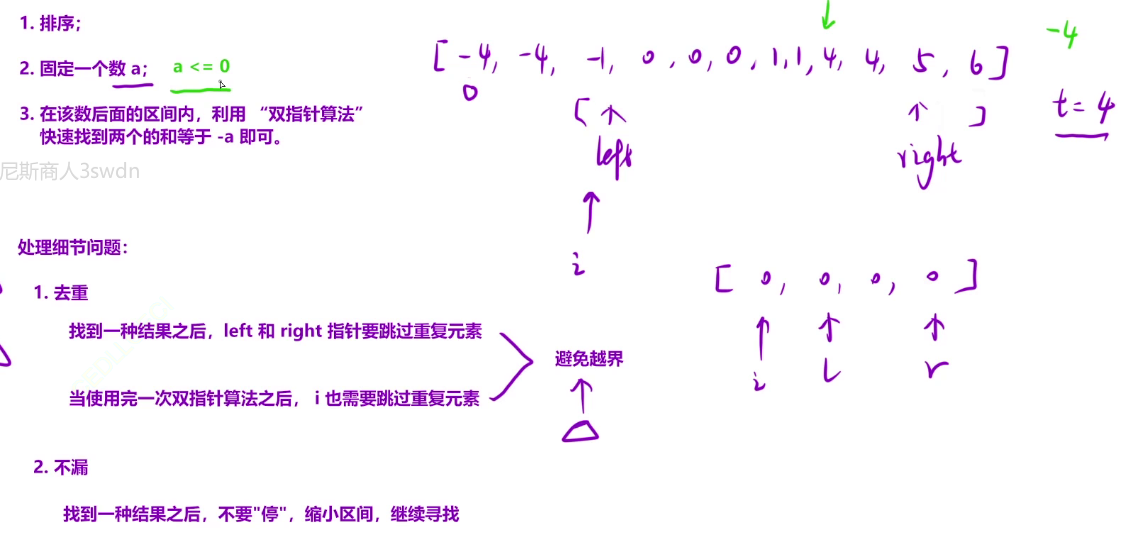
- 「去重」操作:
- 找到⼀个结果之后, left 和 right 指针要「跳过重复」的元素;
- 当使⽤完⼀次双指针算法之后,固定的 a 也要「跳过重复」的元素 ;(-4 -4)
- 去重操作移动指针时,要避免越界(【0,0,0,0,】)
- 不漏操作
- 找到一种结果后,双指针不要听继续缩小空间寻找
- (常数级别的小优化)固定数字a时,只需要固定a<0的数,因为数组经过排序后,后面的正数无论怎么组合也不会出现负数的情况,所以只需要固定a<0的数
代码实现
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums)
{
vector<vector<int>> ret;
// 1. 排序
sort(nums.begin(), nums.end());
// 2. 利⽤双指针解决问题
int n = nums.size();
for(int i = 0; i < n; ) // 固定数 a
{
if(nums[i] > 0) break; // ⼩优化
int left = i + 1, right = n - 1, target = -nums[i];
while(left < right)
{
int sum = nums[left] + nums[right];
if(sum > target) right--;
else if(sum < target) left++;
else
{
//大括号会直接形成vector<int>数组,存储到ret里
ret.push_back({nums[i], nums[left], nums[right]});
//不漏
left++, right--;
// 去重操作 left 和 right 且 避免越界
while(left < right && nums[left] == nums[left - 1]) left++;
while(left < right && nums[right] == nums[right + 1])
right--;
}
}
/* 去重 i 且i也不能越界(这里先让i移动下一个位置,然后去之前的值比较
若相等,继续移动。我们这里去重操作在for循环最后,所以为避免多++一个位置
删除for循环里的++ */
i++;
while(i < n && nums[i] == nums[i - 1]) i++;
}
return ret;
}
};
四数之和
四数之和
题目解析
与三数之和类似
算法原理
- 解法一:排序+暴力枚举+set去重
- 解法二:排序+双指针
先依次固定一个数记为a,剩余后面的数利用**“ 三数之和“**的思想,找到三个数,使其和为target-a。
依次固定一个数b,在b后面的区间,利用双指针找到使其和为target-a-b.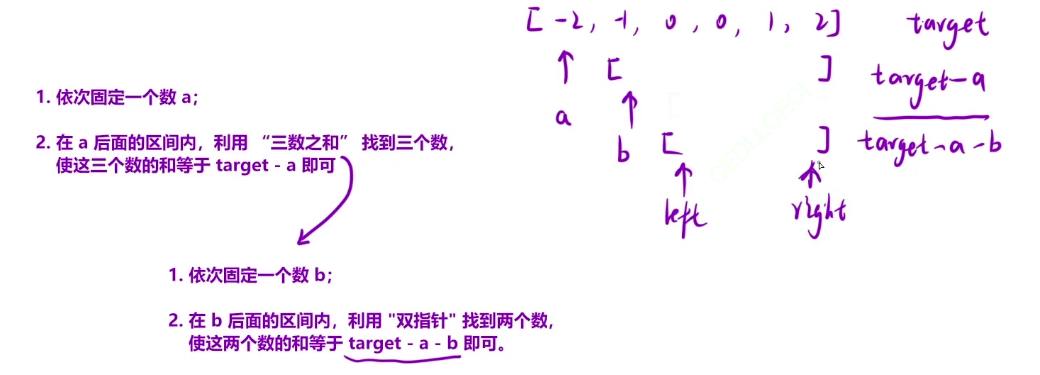
同样需要处理细节问题:不重、不漏
- 不重(3个地方)
- 当left和right找到结果时,要跳过相同的数
- 当利用完双指针寻找完之后,b也要跳过相同的数
- 当找出三数之和后,a也要跳过相同的数
- 不漏:在我们利用双指针寻找结果为target-a-b时,当找到一个结果时,不要停继续缩小区间寻找结果
代码实现
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
//定义结果数组
vector<vector<int>> ret;
//1.排序
sort(nums.begin(),nums.end());
//2.利用双指针
int n = nums.size();
for(int i = 0;i < n;) //固定a
{
//利用三数之和
for(int j = i+1;j<n;) //固定b
{
int left = j + 1,right = n-1;
long long aim =(long long) target-nums[i]-nums[j]; //目标值target-a-b //这里提交leetcode会提示数据溢出的错误,换成longlong
while(left<right)
{
int sum = nums[left]+nums[right];
if(sum < aim) left++;
else if(sum > aim) right--;
else
{
ret.push_back({nums[i],nums[j],nums[left],nums[right]});
//找到之后继续缩小区间防止漏
left++;
right--;
//去重一双指针
while(left<right && nums[left] == nums[left-1]) left++;
while(left<right && nums[right] == nums[right+1]) right--;
}
}
//去重二b
j++;
while(j<n && nums[j]==nums[j-1]) j++;
}
//去重a
i++;
while(i<n && nums[i] == nums[i-1]) i++;
}
return ret;
}
};
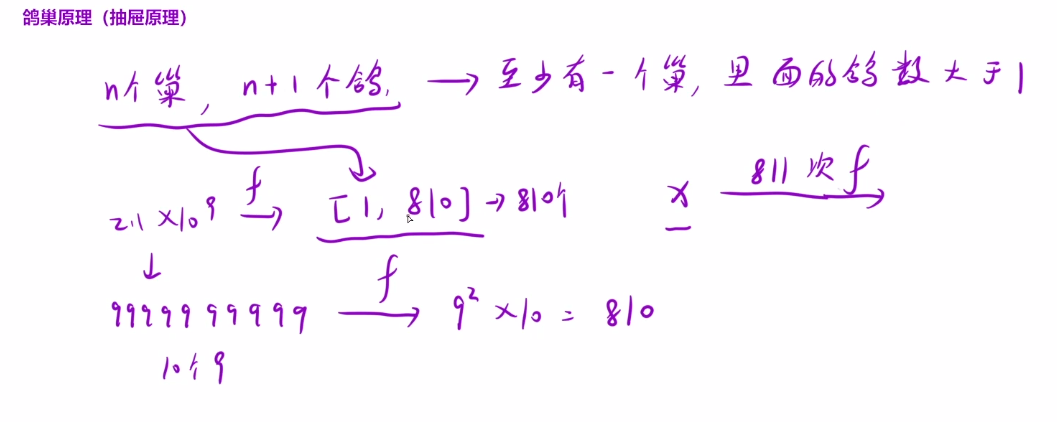










![P9240 [蓝桥杯 2023 省 B] 冶炼金属(比值问题)](https://img-blog.csdnimg.cn/f6191c405ad24092aabcf9e0b35a23ad.png)