deepin-terminal
安装
源里面自带了这个软件，可以直接装
sudo apt install deepin-terminal启动
按下Win键，输入deep即可快速检索出图标，点击启动
效果
分屏
Ctrl+Shift+H 水平分割
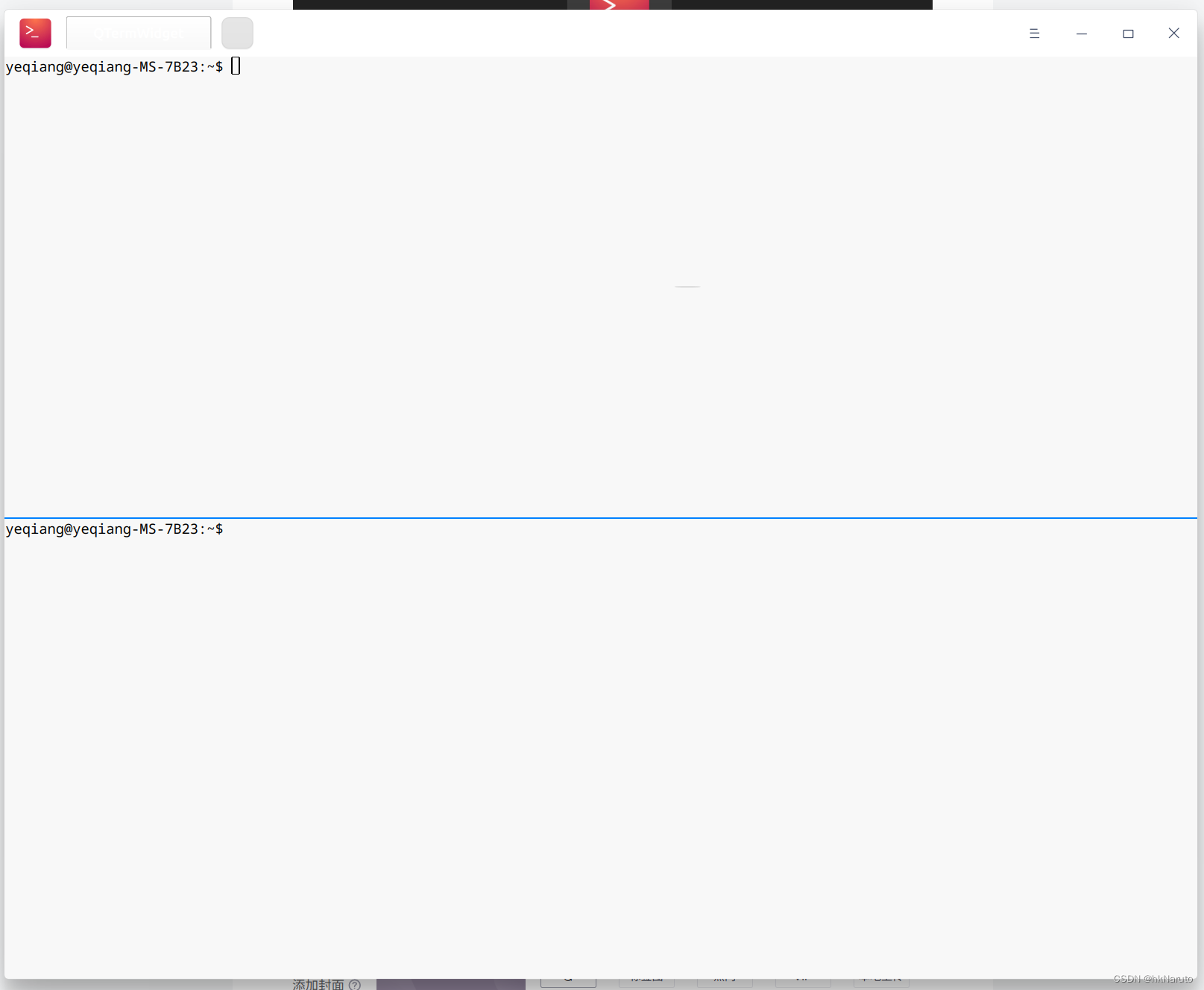
Ctrl+Shift+J 垂直分割
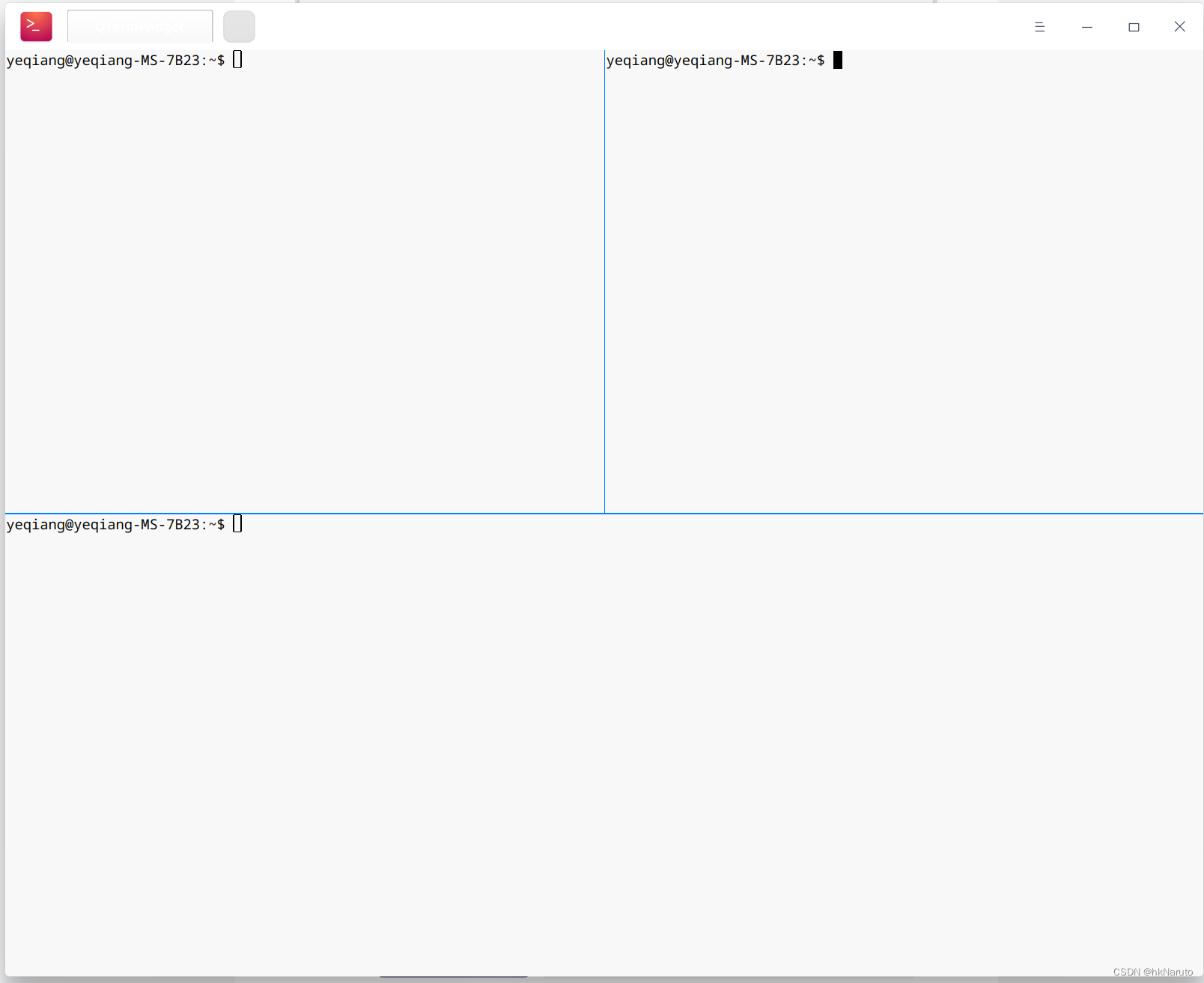
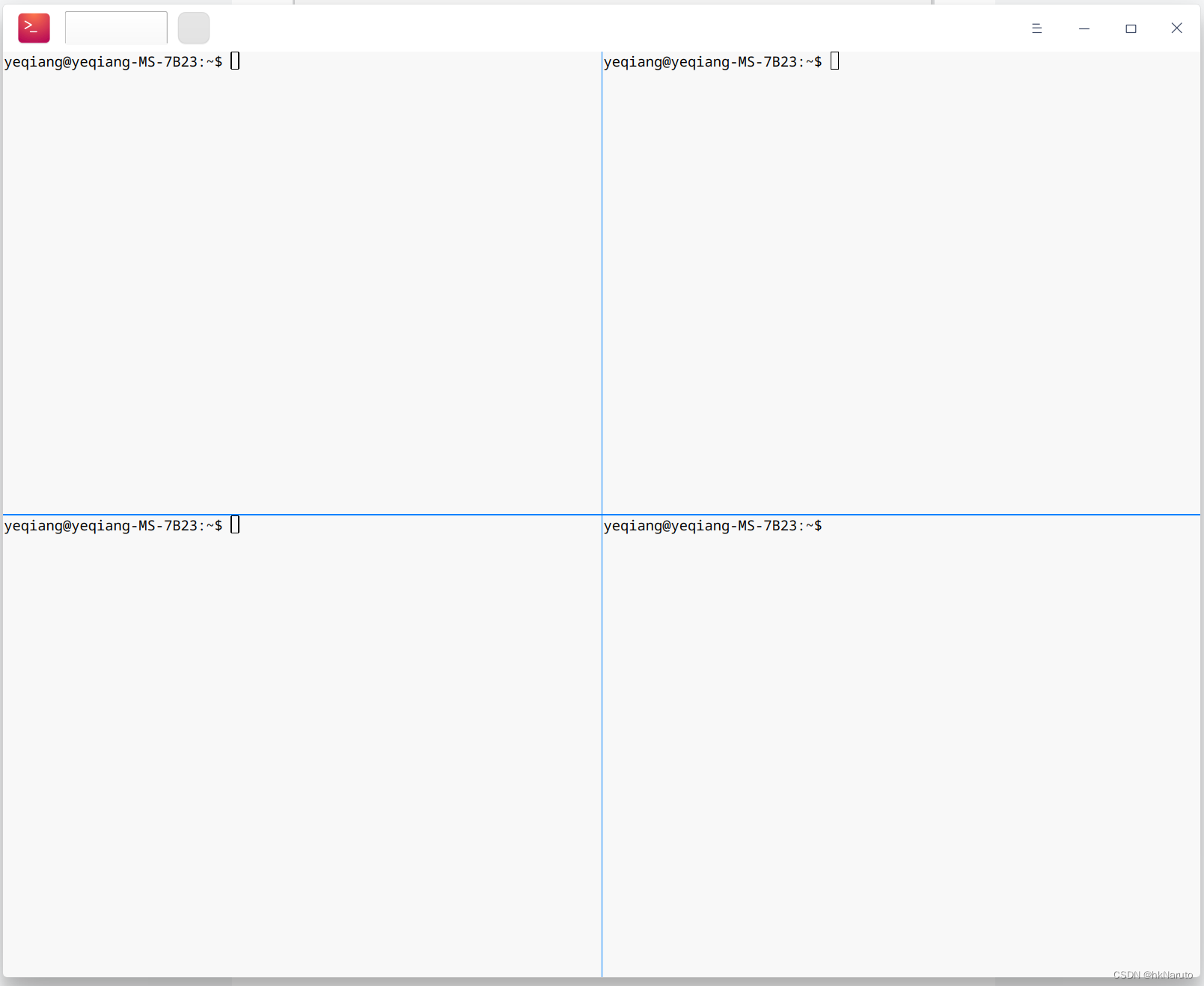
最多分割成四个小窗口，鼠标点击可以切换不同窗口
适配不好，背景颜色等都不能设置
Ubuntu 22.03 LTS 安装deepin-terminal 实现 终端 分屏
news2024/11/15 5:45:40
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1261406.html
如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！相关文章
Flask Echarts 实现历史图形查询
Flask前后端数据动态交互涉及用户界面与服务器之间的灵活数据传递。用户界面使用ECharts图形库实时渲染数据。它提供了丰富多彩、交互性强的图表和地图，能够在网页上直观、生动地展示数据。ECharts支持各种常见的图表类型，包括折线图、柱状图、饼图、散点…
深度剖析API接口测试工具的企业价值
随着企业软件开发的日益复杂和互联网应用的普及，API接口成为不同软件系统之间信息传递的桥梁。在这一背景下，API接口测试工具的应用变得愈加重要，对企业的发展和软件质量起到了关键性的作用。本文将深入探讨API接口测试工具在企业中的重要性&…
进程（4）——进程地址空间【linux】
进程（4）——进程地址空间【linux】 一.什么是进程地址空间二.进程地址空间不是真实地址？三.物理地址与进程地址空间的关系（整体部分）四. 细节4.1 进程地址空间的本质：4.2 为什么要有进程地址空间࿱…
机器学习——多元线性回归升维
机器学习升维 升维使用sklearn库实现特征升维实现天猫年度销量预测实现中国人寿保险预测 升维 定义：将原始的数据表示从低维空间映射到高维空间。在线性回归中，升维通常是通过引入额外的特征来实现的，目的是为了更好地捕捉数据的复杂性&#…
MacOS 系统 Flutter开发Android 环境配置
上节我们已经把 开发工具准备齐全，并可以进行Flutter的web开发，本节将做安卓开发环境进行详细说明
接上节这里先说下，系统环境 MacOS14 （Sonoma） 芯片 Apple M3 执行命令：flutter doctor 提示如下&#…
Shell脚本：Linux Shell脚本学习指南（第三部分Shell高级）一
第三部分：Shell高级（一）
这一章讲解 Shell 脚本编程的进阶内容，主要涉及重定向、文件描述符、管道和过滤器、子 Shell、信号等。 本章会使用到一些底层的编程知识，有C语言和 C 编程经验的程序员阅读起来将会更加轻松。…
《微信小程序开发从入门到实战》学习三十三
第四章 云开发
本章云开发技术的功能与使用，包括以下几点：
1.学习使用云开发控制台
2.学习云开发JSON数据库功能
3.学习云开文件存储功能
4.学习云函数功能 5.使用云开发技术实现投票小程序的服务端功能
投票小程序大部分已经实现。需要实现&#…
人工智能-优化算法之凸集
凸性
凸性（convexity）在优化算法的设计中起到至关重要的作用， 这主要是由于在这种情况下对算法进行分析和测试要容易。 换言之，如果算法在凸性条件设定下的效果很差， 那通常我们很难在其他条件下看到好的结果。 此外&…
SHAP（一）：具有 Shapley 值的可解释 AI 简介
SHAP（一）：具有 Shapley 值的可解释 AI 简介
这是用 Shapley 值解释机器学习模型的介绍。 沙普利值是合作博弈论中广泛使用的方法，具有理想的特性。 本教程旨在帮助您深入了解如何计算和解释基于 Shapley 的机器学习模型解释。 我…
NX二次开发UF_CURVE_create_arc_point_tangent_radius 函数介绍
文章作者：里海 来源网站：https://blog.csdn.net/WangPaiFeiXingYuan
UF_CURVE_create_arc_point_tangent_radius
Defined in: uf_curve.h int UF_CURVE_create_arc_point_tangent_radius(tag_t point, tag_t tangent_object, double radius, UF_CURVE_…
初识前后端数据交互(新手篇)
一个软件项目的开发必然是离不开前端和后端的协作，对于刚入行的新手前端或者新手后端来说，很有必要了解一下对方是在做什么，以及提供给自己什么样的帮助，为什么需要对方共同协作才能完成整个软件项目的开发呢？希望这篇…
Scrapy框架内置管道之图片视频和文件(一篇文章齐全)
1、Scrapy框架初识（点击前往查阅）
2、Scrapy框架持久化存储（点击前往查阅）
3、Scrapy框架内置管道
4、Scrapy框架中间件（点击前往查阅） Scrapy 是一个开源的、基于Python的爬虫框架，它提供了…
2015年五一杯数学建模B题空气污染问题研究解题全过程文档及程序
2015年五一杯数学建模
B题 空气污染问题研究
原题再现 近十年来，我国 GDP 持续快速增长，但经济增长模式相对传统落后，对生态平衡和自然环境造成一定的破坏，空气污染的弊病日益突出，特别是日益加重的雾霾天气已经干扰…
从0开始学习JavaScript--JavaScript对象继承深度解析
JavaScript中的对象继承是构建灵活、可维护代码的关键部分。本文将深入讨论JavaScript中不同的继承方式，包括原型链继承、构造函数继承、组合继承等，并通过丰富的示例代码展示它们的应用和差异。通过详细解释，大家可以更全面地了解如何在Java…
Shopee如何入驻？如何防封？
Shopee作为东南亚领航电商平台，面向东南亚蓝海市场，近年来随着东南亚市场蒸蒸日上，虾皮也吸引了大批量的跨境商家入驻。那么接下来就给想要入驻的虾皮小白一个详细的安全入驻教程。 一、商家如何入驻
虾皮与LAZADA最大的区别就是商家即卖家&…
RT-DETR改进 | 2023 | InnerEIoU、InnerSIoU、InnerWIoU、InnerDIoU等二十余种损失函数
论文地址：官方Inner-IoU论文地址点击即可跳转
官方代码地址：官方代码地址-官方只放出了两种结合方式CIoU、SIoU
本位改进地址： 文末提供完整代码块-包括InnerEIoU、InnerCIoU、InnerDIoU等七种结合方式和其AlphaIoU变种结合起来可以达到二十…
15、矩阵键盘密码锁
矩阵键盘密码锁 main.c
#include <REGX52.H>
#include "Delay.h"
#include "LCD1602.h"
#include "MatrixKey.h"//初始化变量
unsigned char KeyNum;
unsigned int Password,Count;void main()
{//LCD屏幕初始化显示Password:LCD_Init();…
kafka的详细安装部署
简介：
Kafka是一个分布式流处理平台，主要用于处理高吞吐量的实时数据流。Kafka最初由LinkedIn公司开发，现在由Apache Software Foundation维护和开发。
Kafka的核心是一个分布式发布-订阅消息系统，它可以处理大量的消息流&#…
matplotlib,DLL load failed: 找不到指定的模块
问题：import matplotlib mportError: DLL load failed: 找不到指定的模块
（2023年11月28日） 解决方法：具体是matplotlib版本不匹配，而且在线pip install numpy时因为在线下载numpy库中缺少DLL。 应该下载带有mkl的num…