二叉堆与优先队列
1、什么是二叉堆
1.1、初识二叉堆
什么是二叉堆?
二叉堆本质上是一种完全二叉树,它分为两个类型。
-
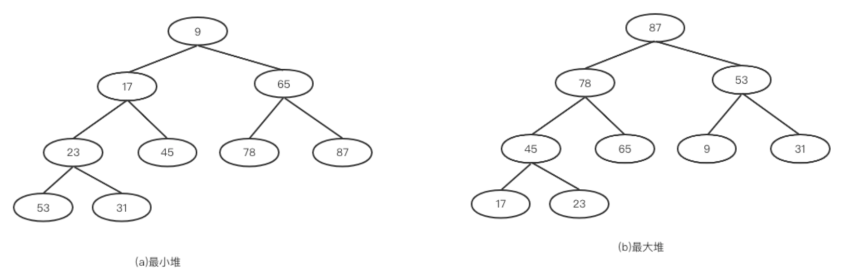
最大堆(也叫大顶堆):任意节点的值都大于或等于它的左右孩子节点的值,并且最大的值位于堆顶,即根节点处。
-
最小堆(也叫小顶堆):任意节点的值都小于或等于它的左右孩子节点的值,并且最小的值位于堆顶,即根节点处。
二叉堆的根节点叫做堆顶。
最大堆和最小堆的特点决定了:最大堆的堆顶是整个堆中的最大元素;最小堆的堆顶是整个堆中的最小元素。
1.2、二叉堆的自我调整
对于二叉堆,有如下的几种操作:
- 插入节点。
- 删除节点。
- 构建二叉堆。
这几种操作都是基于堆的自我调整,即把一个不符合堆性质的完全二叉树,调整成一个堆。下面以最小堆为例,来看一看二叉堆是如何进行自我调整的。
1.2.1、插入节点
当二叉堆插入新节点时,插入的位置是完全二叉树的最后一个位置。例如插入一个新节点0.
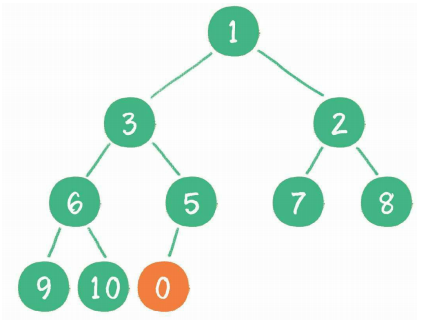
这时新节点的父节点5比0大,不符合最小堆的性质,于是让新节点0上浮,和父节点交换位置。
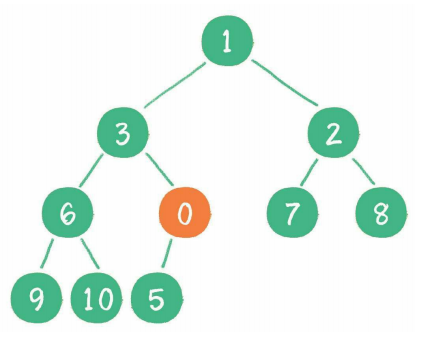
继续用节点0和它现在的父节点3比较,因为比3小,所以新节点0继续上浮。
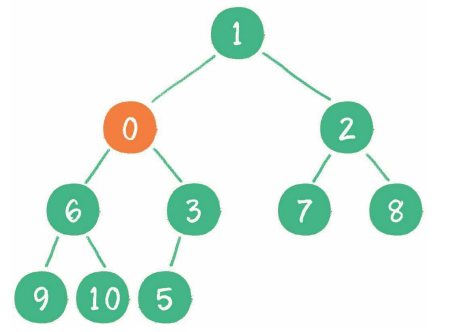
继续比较,最终新节点0上浮到了堆顶位置。
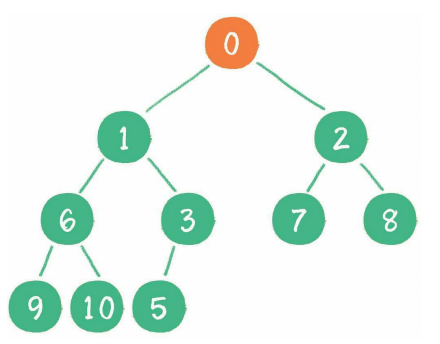
总结一下堆插入元素的规则:将元素插入到保持其为完全二叉树的最后一个位置,然后顺着这条支路一直向上调整,每前进一层就要保证其子树都满足堆否则就去处理子树,直到完全满足要求。
1.2.2、删除节点
堆本身比较特殊,一般对堆中的数据进行操作都是针对堆顶的元素,即每次都是从堆中获得最大值或最小值,其他的不关心,所以删除节点的时候,也是删除堆顶。
例如删除最小堆的堆顶1
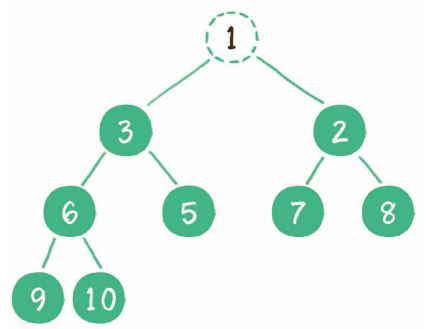
这时,为了继续维持完全二叉树的结构,我们会把堆的最后一个节点10临时补到原本堆顶的位置。
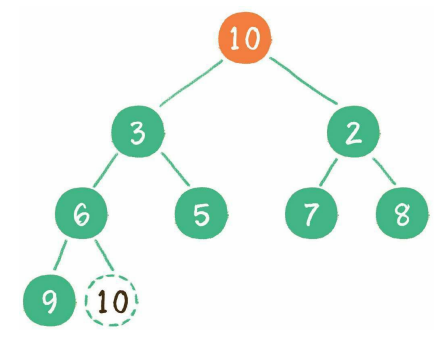
接下来,让暂处堆顶的节点和它的左右孩子进行比较,如果左右孩子节点中最小的一个比节点10小,那么让节点10下沉。
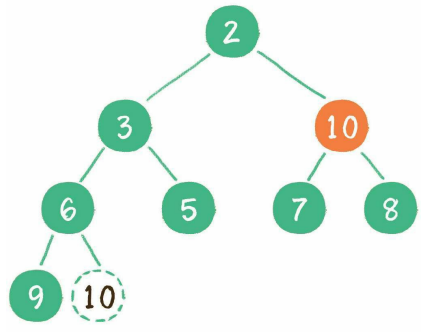
继续比较节点10与其孩子节点,继续下沉,直到满足最小堆要求
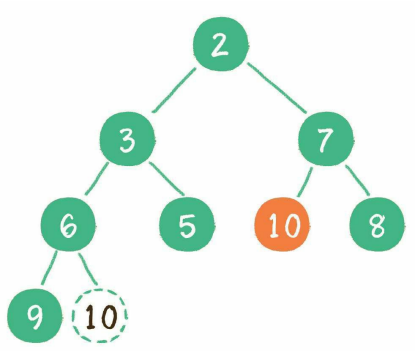
这样一来,二叉堆重新得到了调整。
1.2.3、构建二叉堆
构建二叉堆,就是把一个无序的完全二叉树调整为二叉堆,本质就是让所有非叶子节点依次下沉。
下面举一个无序完全二叉树构造成二叉堆的例子,如下图所示。
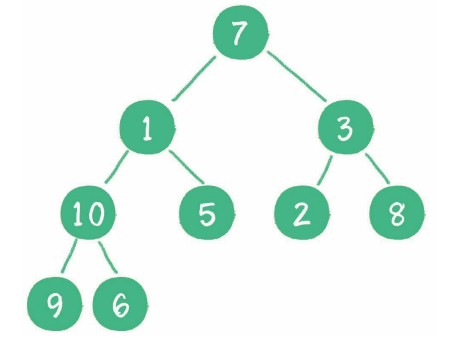
首先,从最后一个非叶子节点开始,也就是从节点10开始。如果节点10大于它左、右孩子节点中最小的一个,则节点10“下沉”。
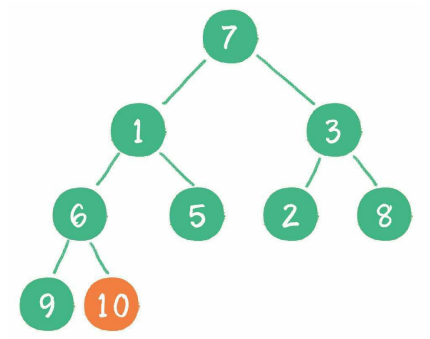
接下来轮到节点3,如果节点3大于它左、右孩子节点中最小的一个,则节点3“下沉”。
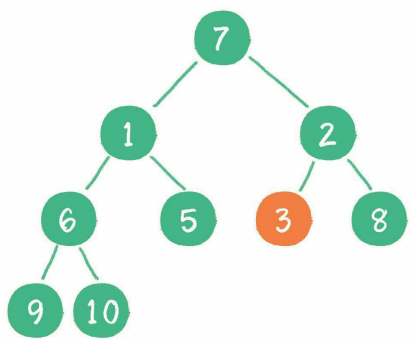
然后轮到节点1,如果节点1大于它左、右孩子节点中最小的一个,则节点1“下沉”。事实上节点1小于它的左、右孩子,所以不用改变。
接下来轮到节点7,如果节点7大于它左、右孩子节点中最小的一个,则节点7“下沉”。
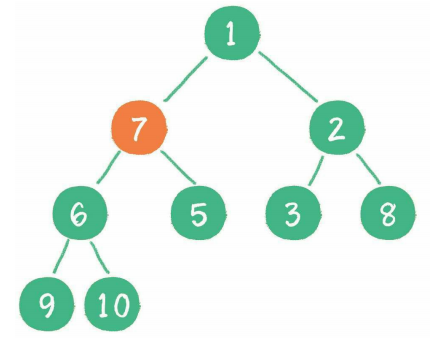
节点7继续比较,继续“下沉”。
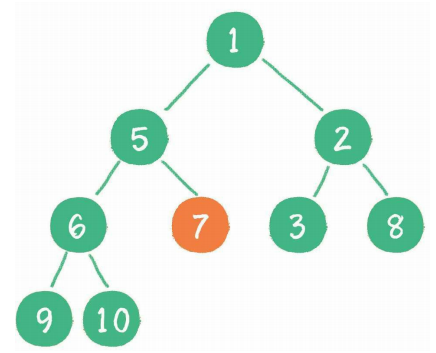
经过上述几轮比较和“下沉”操作,最终每一节点都小于它的左、右孩子节点,一个无序的完全二叉树就被构建成了一个最小堆。
1.3、二叉堆的代码实现
二叉堆虽然是一个完全二叉树,但它的存储方式并不是链式存储,而是顺序存储。换句话说,二叉堆的所有节点都存储在数组中。
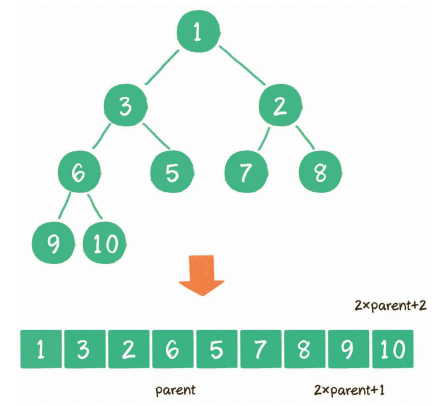
我们可以通过数组的下标来定位父节点和左右孩子节点。
假设一个节点的下标为i:
- 当 i = 0 时,为根节点。
- 当 i >= 1 时,父节点为(i - 1) / 2。
- 左孩子节点为2 * i + 1,右孩子节点为2 * i + 2。
二叉堆具体的操作代码如下:
/**
* “上浮”调整
* @param array 待调整的堆
*/
public static void upAdjust(int[] array) {
int childIndex = array.length-1;
int parentIndex = (childIndex-1)/2;
// temp 保存插入的叶子节点值,用于最后的赋值
int temp = array[childIndex];
while (childIndex > 0 && temp < array[parentIndex]){
//无须真正交换,单向赋值即可
array[childIndex] = array[parentIndex];
childIndex = parentIndex;
parentIndex = (parentIndex-1) / 2;
}
array[childIndex] = temp;
}
/**
* “下沉”调整
* @param array 待调整的堆
* @param parentIndex 要“下沉”的父节点
* @param length 堆的有效大小
*/
public static void downAdjust(int[] array, int parentIndex, int length) {
// temp 保存父节点值,用于最后的赋值
int temp = array[parentIndex];
int childIndex = 2 * parentIndex + 1;
while (childIndex < length) {
// 如果有右孩子,且右孩子小于左孩子的值,则定位到右孩子
if (childIndex + 1 < length && array[childIndex + 1] < array[childIndex]) {
childIndex++;
}
// 如果父节点小于任何一个孩子的值,则直接跳出
if (temp <= array[childIndex])
break;
//无须真正交换,单向赋值即可
array[parentIndex] = array[childIndex];
parentIndex = childIndex;
childIndex = 2 * childIndex + 1;
}
array[parentIndex] = temp;
}
/**
* 构建堆
* @param array 待调整的堆
*/
public static void buildHeap(int[] array) {
// 从最后一个非叶子节点开始,依次做“下沉”调整
for (int i = (array.length-2)/2; i>=0; i--) {
downAdjust(array, i, array.length);
}
}
代码中有一个优化的点,就是在父节点和孩子节点做连续交换时,并不一定要真的交换,只需要先把交换一方的值存入temp变量,做单向覆盖,循环结束后,再把temp的值存入交换后的最终位置即可。
2、什么是优先队列
2.1、优先队列的特点
优先队列:说到底还是一种队列,他的工作就是poll()/peek()出队列中最大/最小的元素,所以叫带有优先级的队列。能够实现优先功能的策略不一定只有堆,例如二顶堆、平衡树、线段树、C++里会用二进制分组的vector来实现一个优先队列。
2.2、实现优先队列
当我们用二叉堆来实现优先队列时,优先队列的入队和出队操作就对应了二叉堆中的插入元素和删除元素,具体的代码如下:
private int[] array;
private int size;
public PriorityQueue(){
//队列初始长度为32
array = new int[32];
}
/**
* 入队
* @param key 入队元素
*/
public void enQueue(int key) {
//队列长度超出范围,扩容
if(size >= array.length){
resize();
}
array[size++] = key;
upAdjust();
}
/**
* 出队
*/
public int deQueue() throws Exception {
if (size <= 0) {
throw new Exception("the queue is empty !");
}
//获取堆顶元素
int head = array[0];
//让最后一个元素移动到堆顶
array[0] = array[--size];
downAdjust();
return head;
}
/**
* “上浮”调整
*/
private void upAdjust() {
int childIndex = size-1;
int parentIndex = (childIndex-1)/2;
// temp 保存插入的叶子节点值,用于最后的赋值
int temp = array[childIndex];
while (childIndex > 0 && temp > array[parentIndex]) {
//无须真正交换,单向赋值即可
array[childIndex] = array[parentIndex];
childIndex = parentIndex;
parentIndex = parentIndex / 2;
}
array[childIndex] = temp;
}
/**
* “下沉”调整
*/
private void downAdjust() {
// temp 保存父节点的值,用于最后的赋值
int parentIndex = 0;
int temp = array[parentIndex];
int childIndex = 1;
while (childIndex < size) {
// 如果有右孩子,且右孩子大于左孩子的值,则定位到右孩子
if (childIndex + 1 < size && array[childIndex + 1] > array[childIndex]) {
childIndex++;
}
// 如果父节点大于任何一个孩子的值,直接跳出
if (temp >= array[childIndex])
break;
//无须真正交换,单向赋值即可
array[parentIndex] = array[childIndex];
parentIndex = childIndex;
childIndex = 2 * childIndex + 1;
}
array[parentIndex] = temp;
}
/**
* 队列扩容
*/
private void resize() {
//队列容量翻倍
int newSize = this.size * 2;
this.array = Arrays.copyOf(this.array, newSize);
}