一，ArrayList的缺陷

1.空间浪费

在之前的博客中，我利用源码详细的讲解了ArrayList这个集合类（尤其是扩容机制），可以知道ArrayList的底层主要是一个动态的可变数组，容量满的时候需要进行1.5倍扩容。但是我们现在考虑这样一个问题，假设ArrayList底层数组的容量是100，我们需要存放101个元素时，当存放第101个元素时需要1.5倍扩容（扩容之后的容量是150），此时势必会造成49个存储空间的浪费！

2.时间开销大

ArrayList底层是一个数组，当我们对顺序表进行插入和删除时，需要移动大量的元素，大大提高了时间复杂度，所以可以看出ArrayList并不适用于进行大量插入和删除的操作。

针对上述ArrayList的两大缺陷，Java是否提供了其他的集合类或者数据结构来解决呢？

1.进行元素扩容时能否根据需求来进行扩容，需要多少空间就去申请多少空间；

2.在进行插入和删除的时候，可不可以不需要移动大量元素。

今天所要介绍的LinkedList集合类和链表的数据结构将很好的解决这两个问题！！！

二，链表

2.1 链表的概念

相对于顺序表，链表是一种在逻辑上连续，在存储上不一定连续的数据结构。其中链表每个元素之间的逻辑关系是通过引用来实现的。

链表中的每一个元素称为一个节点，每一个节点至少包含两类数据：

1.数据域（存放该节点的数据信息）

2.节点域（实现链表节点与节点之间的逻辑关系，对于单链表来说只需要存储一个next即可（存储下一个节点的地址），对于双链表来说则需要存储next和prev（分别存储下一个节点和前一个节点的地址））

2.2 链表的分类

1.单向或者双向

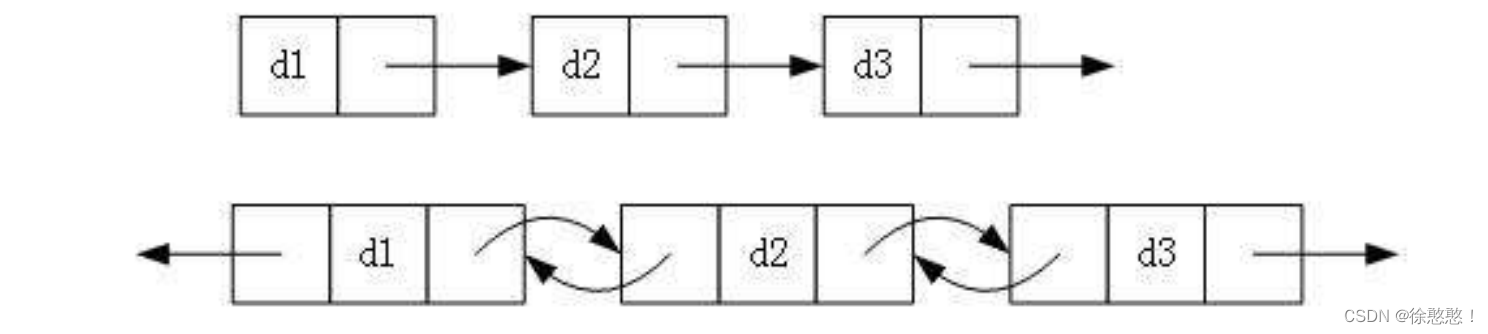
2.带头或者不带头

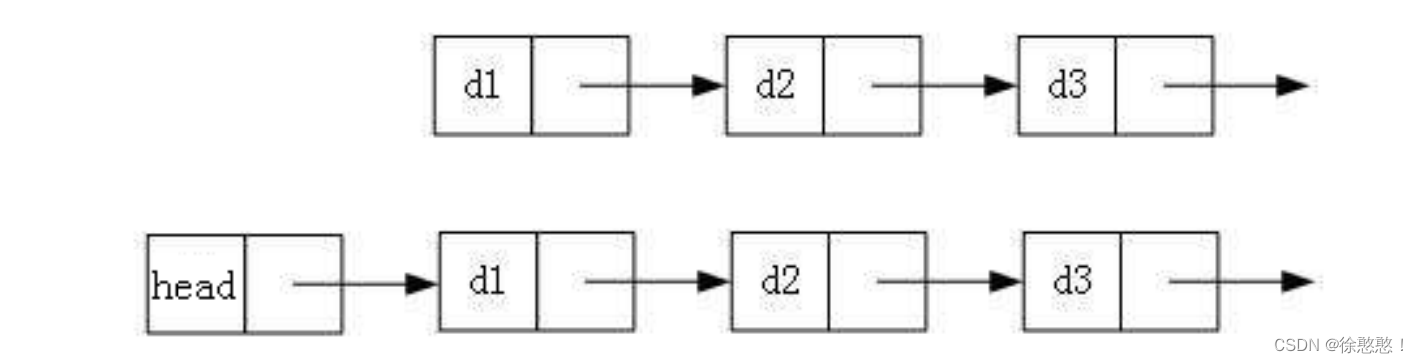
3.循环或者非循环

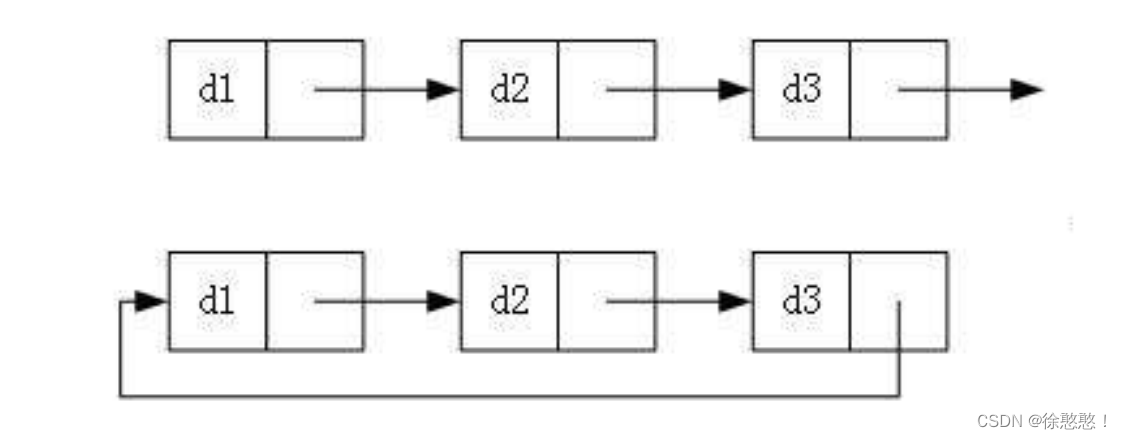
我们只需要重点掌握两种即可：

1.无头单向非循环链表（因为笔试的OJ题中经常会考）；

2.无头双向链表（因为LinkedList的底层就是不带头的双链表）。 

三，顺序表和链表的区别

不同点	ArrayList	LinkedList
存储空间上	物理上一定连续	逻辑上连续，但物理上不一定连续
随机访问	支持： O(1)	不支持： O(N)
头插	需要搬移元素，效率低 O(N)	只需修改引用的指向，时间复杂度为 O(1)
插入	空间不够时需要扩容	没有容量的概念
应用场景	元素高效存储 + 频繁访问	任意位置插入和删除频繁

四，无头单向非循环链表的实现

定义一个MySingleList类来实现单链表的方法，用TestMySingleList类来测试MySingleList类的方法

import java.util.List;

public class MySingleList {
    static class ListNode {
        public int val;
        public ListNode next;

        public ListNode(int val) {
            this.val = val;
        }
    }

    ListNode head;//第一节点的引用，默认为null

    //打印链表
    public void display() {
        ListNode cur = this.head;
        while (cur != null) {
            System.out.print(cur.val + " ");
            cur = cur.next;
        }
        System.out.println();
    }

    //获取链表长度
    public int size() {
        ListNode cur = this.head;
        int count = 0;
        while (cur != null) {
            count++;
            cur = cur.next;
        }
        return count;
    }

    //头插法
    public void addFirst(int data) {
        ListNode node = new ListNode(data);
        node.next = this.head;
        this.head = node;
    }

    //尾插法
    public void addLast(int data) {
        ListNode node = new ListNode(data);
        ListNode cur = this.head;
        if (this.head == null) {
            this.head = node;
        } else {
            while (cur.next != null) {
                cur = cur.next;
            }
            //此时已经处于尾节点
            cur.next = node;
        }
    }

    //任意index位置插入（假设第一个节点的下表为0）
    public void add(int index, int data) {
        //判断index位置的合法性
        if (index < 0 || index > size()) {
            System.out.println("index位置不合法！");//也可以抛异常
        } else if (index == 0) {
            addFirst(data);
        } else if (index == size()) {
            addLast(data);
        } else {
            //1.找到所需插入index位置的前驱
            ListNode cur = findIndexPrev(index);
            //2.修改引用的指向
            ListNode node = new ListNode(data);
            node.next = cur.next;
            cur.next = node;
        }
    }

    private ListNode findIndexPrev(int index) {
        ListNode cur = this.head;
        while (index - 1 != 0) {
            cur = cur.next;
            index--;
        }
        return cur;
    }

    //删除第一次出现的关键字key
    public void remove(int key) {
        if (this.head == null) {
            System.out.println("链表为空！");
            return;
        }
        if (this.head.val == key) {
            this.head = this.head.next;
            return;
        }
        ListNode cur = findPrev(key);//找到所需删除关键字key的前驱
        if (cur == null) {
            System.out.println("没有关键字key！");
        } else {
            cur.next = cur.next.next;
        }
    }

    private ListNode findPrev(int key) {
        ListNode cur = this.head;
        while (cur.next != null) {
            if (cur.val == key) {
                return cur;
            }
            cur = cur.next;
        }
        return null;
    }

    //删除所有出现的关键字key
    public void removeAllKey(int key) {
        if (this.head == null) {
            System.out.println("链表为空！");
            return;
        }
        ListNode prev = this.head;
        ListNode cur = this.head.next;
        while (cur != null) {
            if (cur.val == key) {
                prev.next = cur.next;
                cur = cur.next;
            } else {
                prev = cur;
                cur = cur.next;
            }
        }
        if (this.head.val == key) {
            this.head = this.head.next;
        }
    }

    //清空链表
    public void clear() {
        this.head = null;//单链表只需要将指向第一个节点的引用指向null即可
    }
}

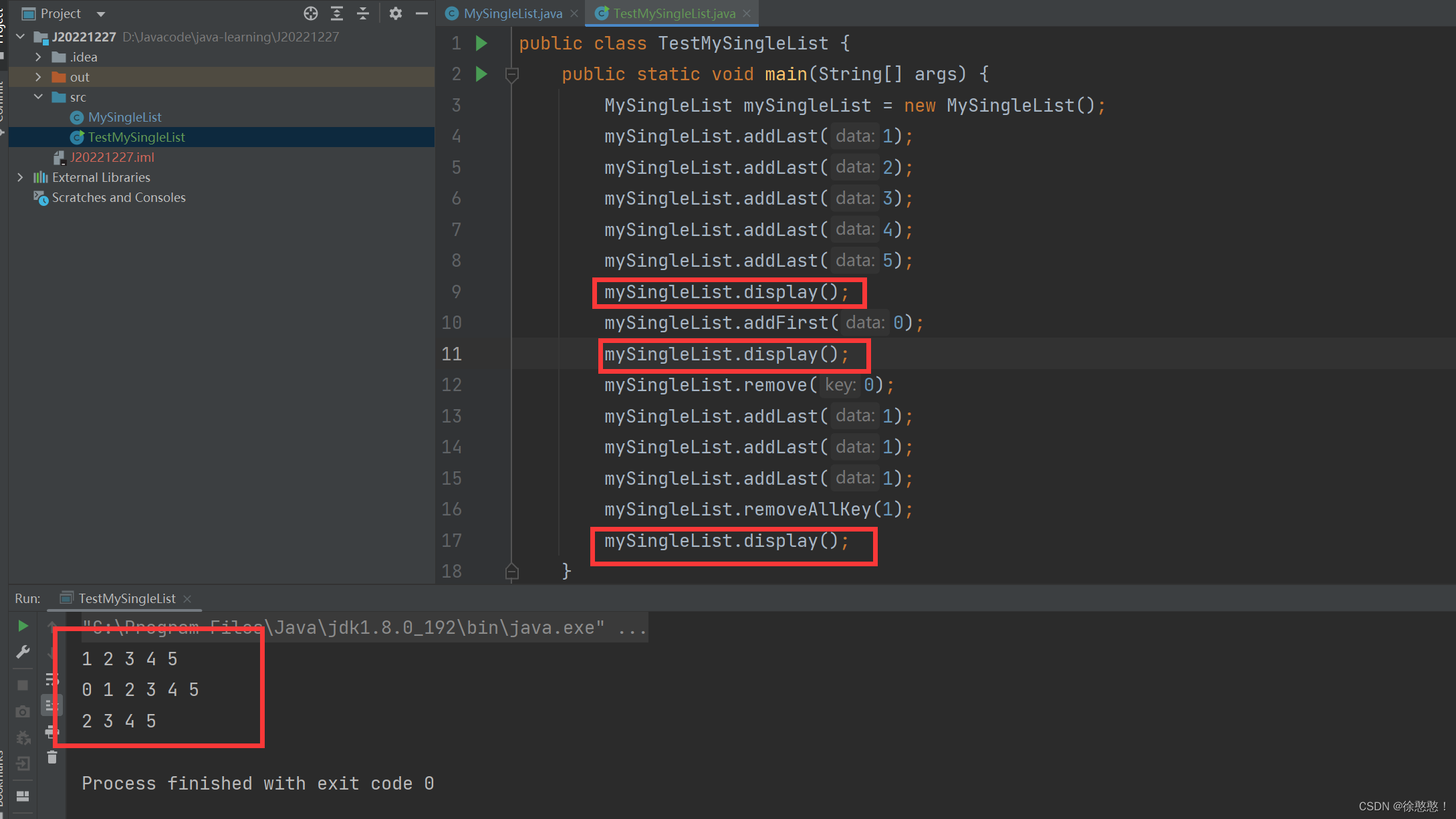
public class TestMySingleList {
    public static void main(String[] args) {
        MySingleList mySingleList = new MySingleList();
        mySingleList.addLast(1);
        mySingleList.addLast(2);
        mySingleList.addLast(3);
        mySingleList.addLast(4);
        mySingleList.addLast(5);
        mySingleList.display();
        mySingleList.addFirst(0);
        mySingleList.display();
        mySingleList.remove(0);
        mySingleList.addLast(1);
        mySingleList.addLast(1);
        mySingleList.addLast(1);
        mySingleList.removeAllKey(1);
        mySingleList.display();
    }
}

 

五，无头双向非循环链表的实现

定义一个MyLinkedList类来实现单链表的方法，用TestMyLinkedList类来测试MyLinkedList类的方法

public class MyLinkedList {
    static class ListNode {
        public int val;
        public ListNode prev;
        public ListNode next;

        public ListNode(int val) {
            this.val = val;
        }
    }

    ListNode head;//定义一个头引用，默认为null
    ListNode tail;//定义一个尾引用，默认为null

    //打印链表
    public void display() {
        ListNode cur = this.head;
        while (cur != null) {
            System.out.print(cur.val + " ");
            cur = cur.next;
        }
        System.out.println();
    }

    //获取链表长度
    public int size() {
        ListNode cur = this.head;
        int count = 0;
        while (cur != null) {
            count++;
            cur = cur.next;
        }
        return count;
    }

    //判断链表是否包含某个元素key
    public boolean contains(int key) {
        ListNode cur = this.head;
        while (cur != null) {
            if (cur.val == key) {
                return true;
            }
            cur = cur.next;
        }
        return false;
    }

    //头插法
    public void addFirst(int data) {
        ListNode node = new ListNode(data);
        if (this.head == null) {
            this.head = node;
            this.tail = node;
        } else {
            node.next = this.head;
            this.head.prev = node;
            this.head = node;
        }
    }

    //尾插法
    public void addLast(int data) {
        ListNode node = new ListNode(data);
        if (this.head == null) {
            this.head = node;
            this.tail = node;
        } else {
            this.tail.next = node;
            node.prev = this.tail;
            this.tail = node;
        }
    }

    //任意index位置插入（假设第一个节点的下标为0）
    public void add(int index, int data) {
        //判断index位置的合法性
        if (index < 0 || index > size()) {
            System.out.println("index位置不合法！");//也可以抛异常
        } else if (index == 0) {
            addFirst(data);
        } else if (index == size()) {
            addLast(data);
        } else {
            //1.找到index位置的节点
            ListNode cur = findIndexPrev(index);
            //2.修改指向的引用
            ListNode node = new ListNode(data);
            node.next = cur;
            node.prev = cur.prev;
            cur.prev.next = node;
            cur.prev = node;
        }
    }

    private ListNode findIndexPrev(int index) {
        ListNode cur = this.head;
        while (index != 0) {
            cur = cur.next;
            index--;
        }
        return cur;
    }

    //删除第一次出现的关键字key
    public void remove(int key) {
        if (this.head == null) {
            System.out.println("链表为空！");
            return;
        }
        ListNode cur = this.head;
        while (cur != null) {
            if (cur.val == key) {
                if (cur == this.head) {
                    this.head = this.head.next;
                    if (this.head != null) {
                        this.head.prev = null;
                    } else {
                        this.tail = null;
                    }
                } else {
                    cur.prev.next = cur.next;
                    if (cur.next != null) {
                        cur.next.prev = cur.prev;
                    } else {
                        this.tail = cur.prev;
                        this.tail.next = null;
                    }
                }
                return;
            }
            cur = cur.next;
        }
    }

    //删除所有出现的关键字key
    public void removeAllKey(int key) {
        if (this.head == null) {
            System.out.println("链表为空！");
            return;
        }
        ListNode cur = this.head;
        while (cur != null) {
            if (cur.val == key) {
                if (cur == this.head) {
                    this.head = this.head.next;
                    if (this.head != null) {
                        this.head.prev = null;
                    } else {
                        this.tail = null;
                    }
                } else {
                    cur.prev.next = cur.next;
                    if (cur.next != null) {
                        cur.next.prev = cur.prev;
                    } else {
                        this.tail = cur.prev;
                        this.tail.next = null;
                    }
                }
            }
            cur = cur.next;
        }
    }

    //清空链表
    public void clear() {
        ListNode cur = this.head;
        while (cur != null) {
            ListNode curNext = cur.next;
            cur.prev = null;
            cur.next = null;
            cur = curNext;
        }
        this.head = null;
        this.tail = null;
    }
}

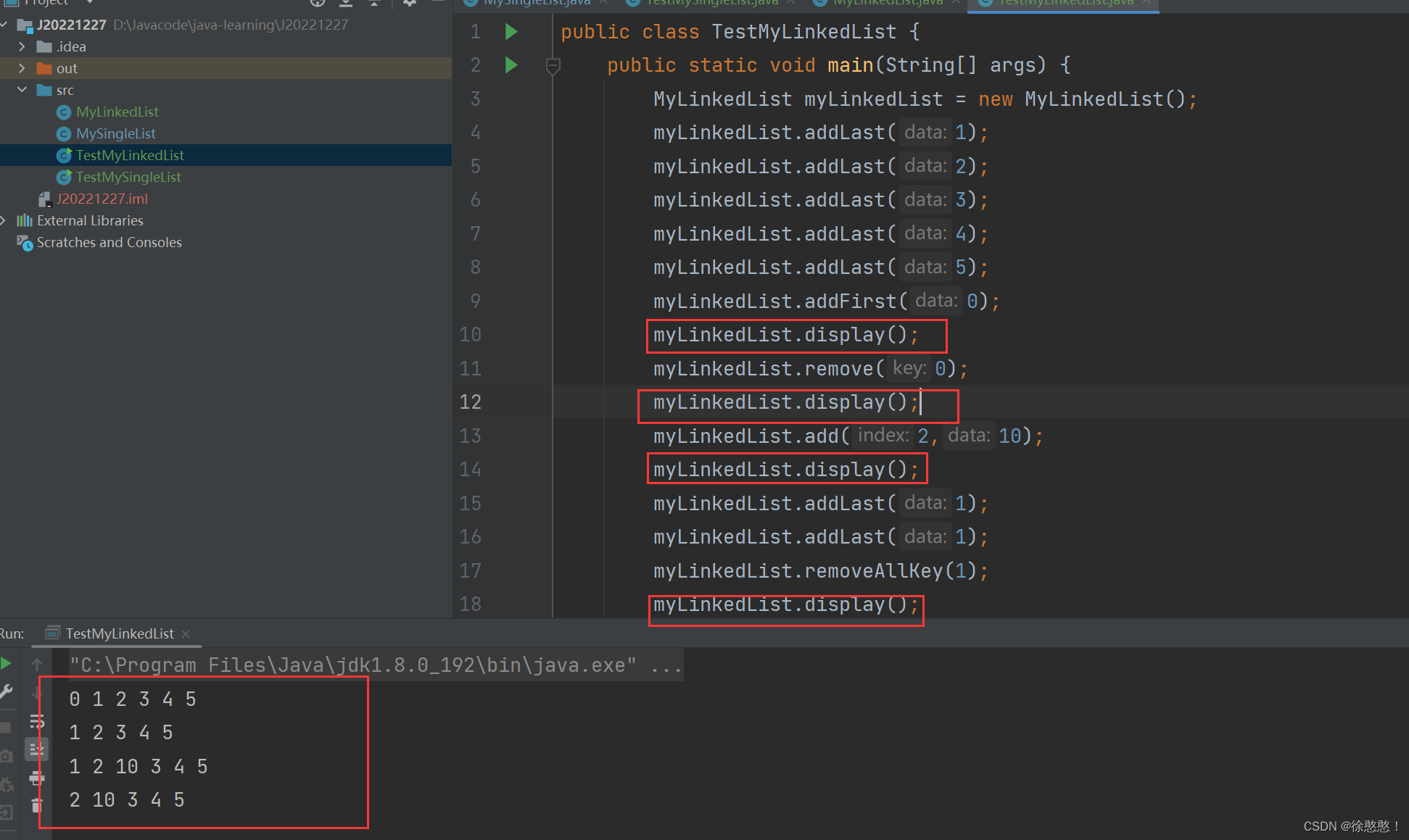
public class TestMyLinkedList {
    public static void main(String[] args) {
        MyLinkedList myLinkedList = new MyLinkedList();
        myLinkedList.addLast(1);
        myLinkedList.addLast(2);
        myLinkedList.addLast(3);
        myLinkedList.addLast(4);
        myLinkedList.addLast(5);
        myLinkedList.addFirst(0);
        myLinkedList.display();
        myLinkedList.remove(0);
        myLinkedList.display();
        myLinkedList.add(2,10);
        myLinkedList.display();
        myLinkedList.addLast(1);
        myLinkedList.addLast(1);
        myLinkedList.removeAllKey(1);
        myLinkedList.display();
    }
}