xx题
甲从1,2,3中抽取一数,记为α;乙从1,2,3,4中抽取一数,记为b规定当a>b或a+1<b时甲获胜,则甲获胜的概率为?
倍数题
若实数a,b,c满足a∶b∶c=1∶2∶5,且a+b+c=24,则a²+b²+c²=?
- 设a = k,b = 2k,c = 5k,带入a + b + c = 24
- k + 2k + 5k = 2;8k = 24;k= 3;
- 带入得a = k = 3 ; b = 2 * 3 = 6; c = 5 * 3 = 15;
- 带入a²+b² + c² = 3² + 6² + 15² = 9 + 36 + 225 = 270.
某公司共有甲、乙两个部门.如果从甲部门调 10 人到乙部门,那么乙部门人数是甲部门的2倍;如果把乙部门员工的言调到甲部门,那么两个部门的人数相等.该公司的总人数为?
- 设甲部门人数为x,乙部分人数y
- 根据条件一可得:2(x-10)= y+10
- 根据条件二可得:
y = x +
y
- 将条件一的xy关系带入条件二计算
- 2(x - 10)= y + 10 ; 2x - 20 = y + 10 ; y = 2x - 30
- 带入条件二 :
y = x +
y ;
(2x - 30) = x +
(2x - 30) ;
x - 24 = x +
-6
x-18 = x ;
x - x = 18 ;
x = 18 ; x = 90
- 带入 y = 2x - 30 = 180 - 30 = 150
- x + y = 90 +150 = 240人
设m,n是小于 20 的质数,满足条件 |m - n| = 2 的{m,n}共有( ).
- 列举出所有20 以内的质数 : 2,3,5,7,11,13,17,19
- 其中 I m - n l = 2的组合有: 3,5 ; 5,7 ; 11,13 ; 17,19 共计四组
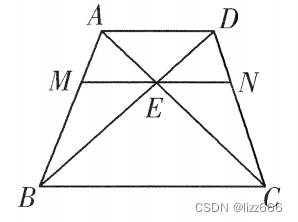
图,BC 是半圆的直径,且 BC=4,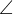 ABC=30°,则图中阴影部分的面积为
ABC=30°,则图中阴影部分的面积为


- 取BC中心点O,连接OA,设a = BO= b = AO = 2,先求等腰三角形ABO面积
- 因为
ABC=30°,所有 C =
AOB= 180° - 30° - 30°= 120°
- 等腰三角形ABO面积 =
* a* b* sinC =
* 2 *2 * sin120° = 2 *
=
- 扇形面积工商 ABO = C * π * a² ÷ 360 =
* π *
=
* π *
=
π
- 即所求阴影面积为等
π -
某人驾车从A地赶往 B地,前一半路程比计划多用时 45 分钟,平均速度只有计划的80%,若后一平路程的平均速度为120千米/小时,此人还能按原定时间到达B地.A,B两地的距离为?
- 从A地到B地计划用时设为t,两地距离为S
- 由前半程可以得出(
+
) * (0.8 *
)=
- 由后半程可以得出(
- 0.75) * 120=
- (
+ 0.75) * 0.8 *
=
算出t = 6
- 带入后半程公式 (
- 0.75) * 120=
- S = 540
如图梯形ABCD的上底与下底分别为5,7,E为AC与BD的交点,MN过点E且平行于AD,则MN = ?
- △AED和△CEB具有相似性,所以对应的边长比例都是5:7
- 即点E到AD的距离与点E到BC的距离之比是5∶7;
- △AME和△ABC具有相似性,且点A到ME的距离与点A到BC的距离之比是5∶(5+7),5:12
- ME =
*BC长度 =
* 7 =
- EN =
,MN = ME + EN =
+
=
线y = ax 与圆( x -a )² + y = 1 相切,则证a² = ?
- 已知直线y = ax与圆(x - a)² + y² = 1相切
- 根据直线和圆相切的条件,直线和圆相切时,圆心到直线的距离等于圆的半径圆心坐标为(a, 0),圆的半径为1, x1=a,y1=0.
- 直线的一般式为:y = ax ,即ax - y = 0,根据Ax1 + By1 + C = 0 可知A = a, B = -1, C = 0
- 其中(x1, y1)是点的坐标
- 点到直线的距离公式为d = |Ax1 + By1 + C| / √(A² + B²) = |Aa + B*0+ C| / √(A² + B²) = |a*a + -1*y + 0| / √(a² + -1²) = |a²| / √(a² + 1) = 1
- 所以
- a² - 1 = 0 ,设a²=z , 得z²-z-1=0
- 根据一元二次方程求解公式
,其中a =1,b=-1,c=-1
=
=
设点A(0,2)和B(1,0)在线段AB上取一点M(x,y)(0<x<1),则以x,y为两边长的矩形面积最大值为?
- 显然过AB两点的直线方程是2x + y - 2 = 0
- 故M(x,y)满足2x + y = 2,y = 2 - 2x
-
矩形面积为边长相乘,S = x * y = x(2-2x) = -2x² +2x
- 要找到面积的最大值,我们可以通过求导数等于零的点来找到。
- 对面积S的x求导 = dx(-2x² +2x) = -4x+2 =0,算的x=
- y = 2 - 2x = 2 -2*
= 2-1 = 1
- S = x * y =
* 1 =
已知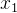 ,
, 是方程x² + ax -1 =0的两个实根,则
是方程x² + ax -1 =0的两个实根,则 +
+  = ?
= ?
- 因为
,
两个实根,一元二次方程根与系数的关系是
+
= -b/a = -a/1 = -a
*
= c/a = -1/1 = -1
- 根据完全平凡公式(a+b)²=a²+2ab+b²、(a-b)²=a²-2ab+b²
- 有
+
,带入(a+b)²=a²+2ab+b²公式
- 可得
+
= (
+
)² - 2
*
= a²+2
某新兴产业在2005年末至2009年末产值的年平均增长率为q,在2009 年末至2013 年 末产值的年平均增长率比前四年下降了40%,2013 年的产值约为2005 年产值的14.46(≈  )倍,则q的值约为?
)倍,则q的值约为?
-
2005 年产值设为a,那么 2009年产值为
-
2013年产值就为
- 2013年产值/2005 年产值 =
=
/a
=
- [(1+q)(1+0.6q)] = 1.95
- 0.6q² + 1.6q - 0.95 = 0 ,两边同时乘100
- 60q² + 160q - 95 = 0
- 一元二次方程
,a =60,b-q =
=
= [-380/120, 60/120] = [-19/6,1/2]
- 抛弃负数,q = 1/2 = 50%
一件工作,甲、乙两人合作需要2天,人工费2900元;乙,丙两人合作需要4天,人工费2600元;甲 、丙两人合作2天完成了全部工作量的5/6,人工费2400 元.甲单独做该工作的时间与人工费分别为
-
设甲独立完成工作需要x天,乙需要y天,丙需要z天
-
2/x + 2/y = 1; 4/y +4/z = 1; 2/x+2/z = 5/6
- x = 2y/(y-2); z =4y/(y-4),带入2/x+2/z = 5/6求解y
- 乙y = 6天,甲x = 2y/(y-2) = 3天, 丙z = 4y/(y-4) = 12天
-
甲人工费为每天a元,乙每天b 元,丙c元,
-
2(a+b)=2900; 4(b+c) =2600 ;2(a+c) = 2400
- a = 1450 - b ; c = 650-b 带入2(a+c) = 2(1450 - b+650-b ) =2400
- b = 450, a= 1000, c =200
- 则甲单独费用为甲天数3*甲费用1000 = 3000元。
某次网球比赛的四强对阵为甲对乙、丙对丁,两场比赛的胜者将争夺冠军.选手之间相互获胜的概率如下,甲获得冠军的概率为?

-
第一局甲获胜的概率是0.3;
-
第二局甲获胜的概率是丙胜(0.3×0.5)+丁胜(0.8×0.5)=0.55
- 即甲最终获胜的概率是0.3×0.55=0.165
平面上有5条平行直线与另一组n条平行直线垂直.若两组平行直线共构成280个矩形,则n=?
- 所有组合
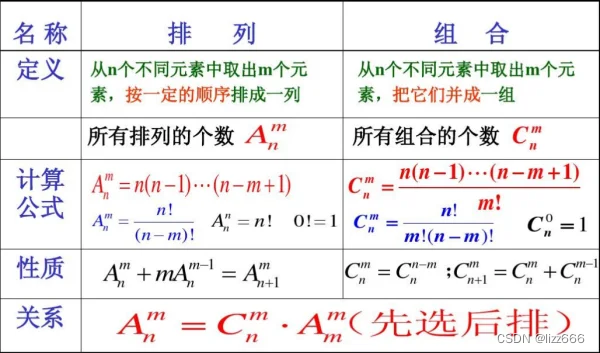
- 然后再取
*
= 280 ;
其中m=2,n=5; 带入公式
=
=
=
= 10
*
= 280 = 10 *
=10 *
- n - 56 = 0;
- 一元二次方程求解
=
=
=
= [-14/2,16/2] = [-7,8]
- 负数去除,n = 8