二分查找法–搜索区间的深入理解

二分查找法是算法学习中很基础的算法，但是其也是很重要的算法，将二分查找法搞明白对后续算法的学习有着事半功倍的作用。

本体难点：二分搜索区间的判断

搜索区间

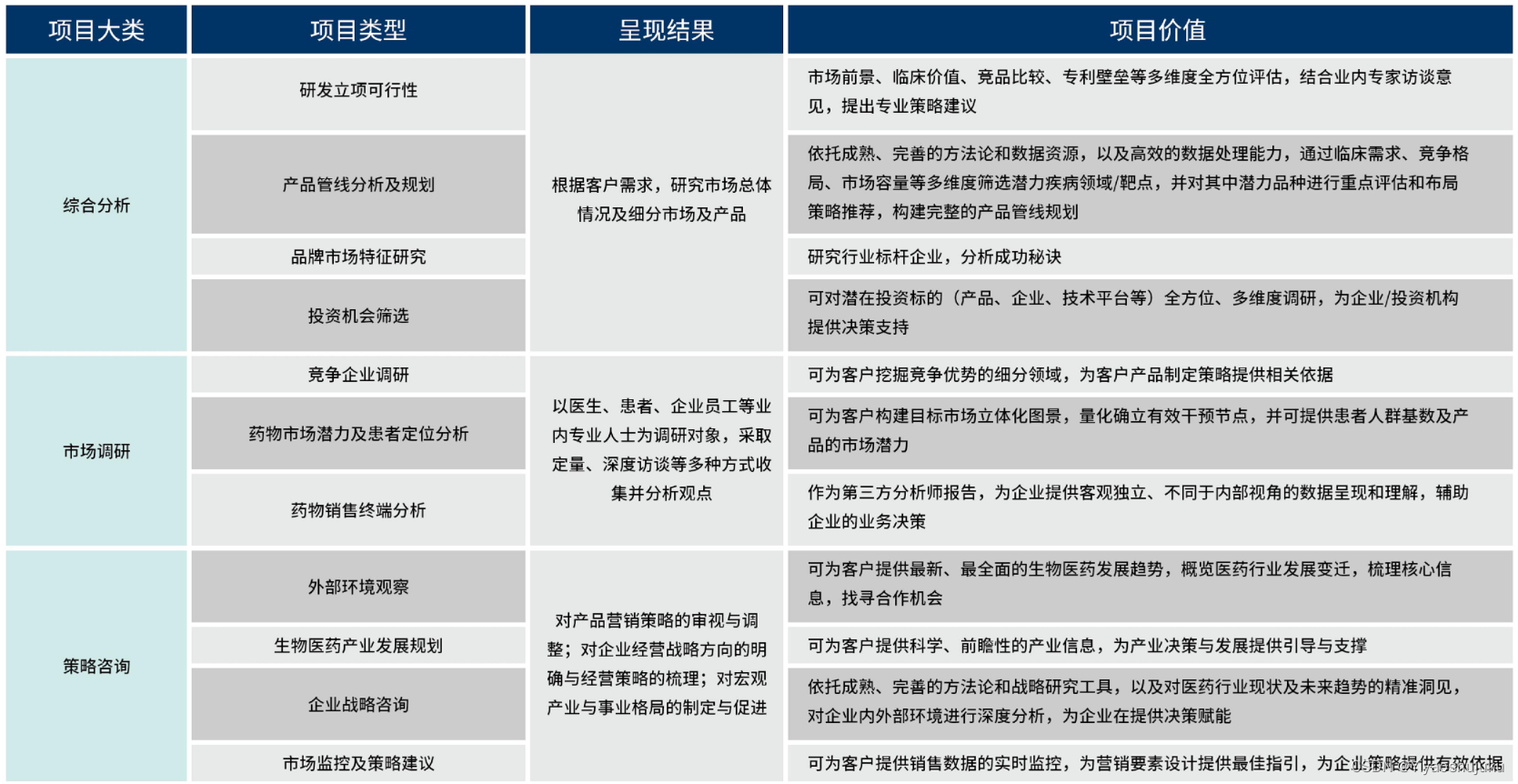
1. [left,right]
   

   int search(vector<int>& nums, int target) {
       int left = 0;
       // [left, right)，right指向的值包含在搜索区间内
       int right = nums.size() - 1;  
       // 判断合法区间
       // 因为搜索区间是[left, right]，故 left==right 为合法搜索的合法区间
       while(left <= right){
           // 防止两个int相加发生溢出
           // int mid = left + (right - left) / 2;
           int mid = (left + right) / 2;
           if(nums[mid] > target)
           	// 搜索区间[left, right]，故right在原搜索区间内。更新搜索区间时，right应该被更新，故high = mid -1
               right = mid - 1;  
           else if(nums[mid] < target) 
          		// 搜索区间[left, right]，故left在原搜索区间内。更新搜索区间时，left应该被更新，故left = mid + 1
               left = mid + 1;
           else return mid;
        }
   	 return -1;
   }
   

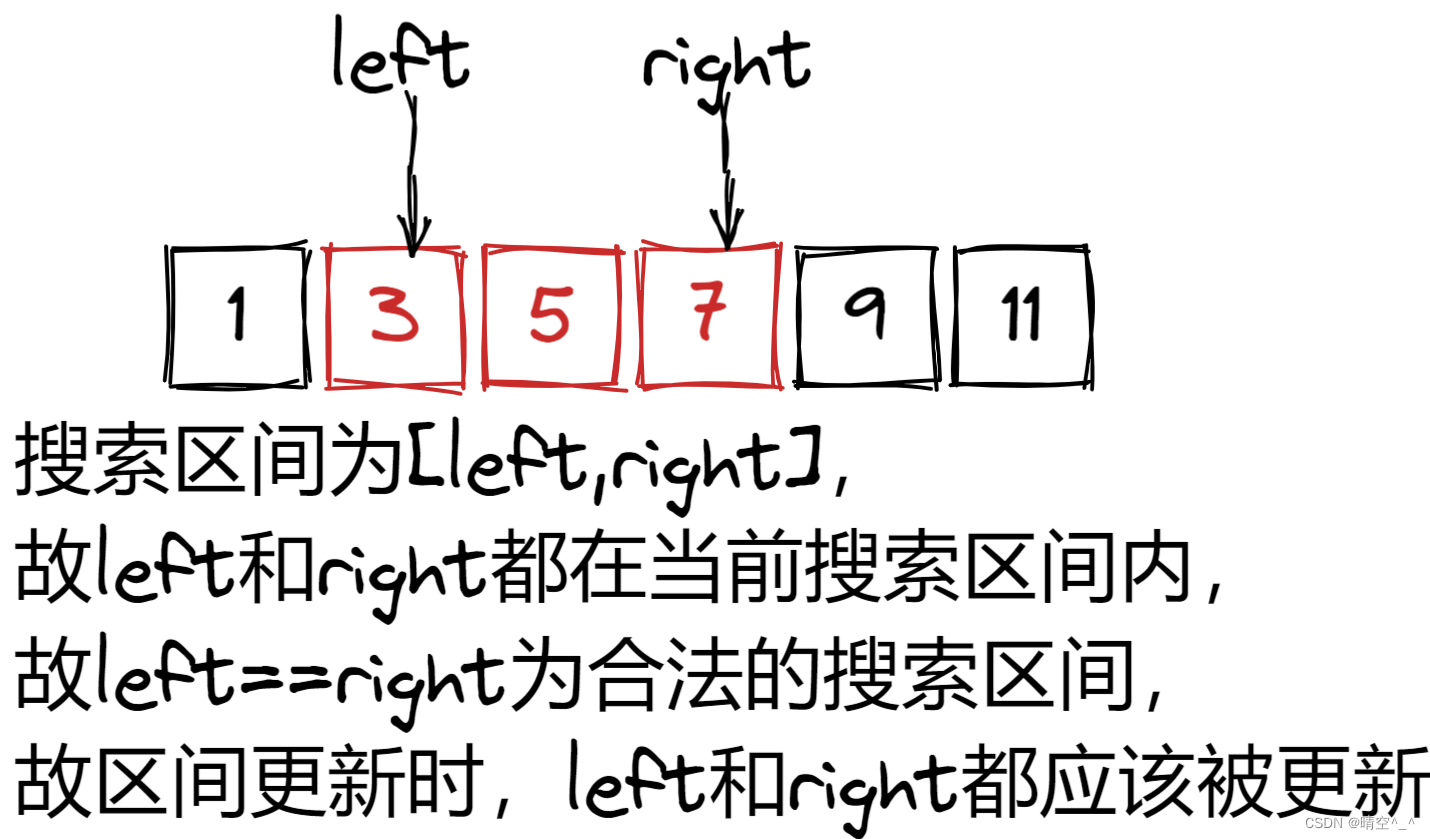
2. [left,right)
   

   int search(vector<int>& nums, int target) {
       int left = 0;
       // [left, right),right指向的值不包含在搜素区间内
       int right = nums.size(); 
       // 判断合法区间
       // 因为搜索区间是[left, right)，故 left==right 为不合法搜索的合法区间
       while(left < right){
           // 防止两个int相加发生溢出
           // int mid = left + (right - left) / 2;
           int mid = (left + right) / 2;
           if(nums[mid] > target)
           	// 搜索区间[left, right)，故right不在原搜索区间内。更新搜索区间时，right“不”应该被更新，故high = mid
               right = mid;  
           else if(nums[mid] < target) 
          		// 搜索区间[left, right]，故left在原搜索区间内。更新搜索区间时，left应该被更新，故left = mid + 1
               left = mid + 1;
           else return mid;
       }
       return -1;
   }
   

3. (right, left) (left, right]

   在算法中不常用，故在此不多做赘述