要求从根节点到叶子结点的最大路径和,可以通过递归遍历二叉树来实现。对于二叉树中的每个节点,我们都可以考虑包含该节点的最大路径和。在递归的过程中,我们需要不断更新全局最大路径和。

具体的思路如下:
-
递归函数设计: 设计一个递归函数,该函数的任务是计算包含当前节点的最大路径和。函数的返回值应该是从当前节点出发到任意叶子节点的最大路径和。
-
递归终止条件: 在递归函数中,需要处理递归的终止条件。当当前节点为 null 时,返回 0,表示空路径的和为 0。
-
递归计算左右子树的最大路径和: 对于当前节点,递归计算左右子树的最大路径和。如果子树的最大路径和为负数,可以选择不包含该子树,将其贡献值设为 0。
-
更新全局最大路径和: 在递归的过程中,不断更新全局最大路径和。全局最大路径和是包含当前节点值的最大路径和,可能由左子树、右子树和当前节点共同组成。
-
返回当前子树的最大路径和: 在递归函数的最后,返回当前子树的最大路径和。
代码示例:
class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
public class MaxPathSum {
int maxSum = Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
if (root == null) {
return 0;
}
// 递归计算左右子树的最大路径和
int leftMax = Math.max(maxPathSum(root.left), 0);
int rightMax = Math.max(maxPathSum(root.right), 0);
// 更新全局最大路径和
maxSum = Math.max(maxSum, root.val + leftMax + rightMax);
// 返回当前子树的最大路径和(只能选择左子树或右子树)
return root.val + Math.max(leftMax, rightMax);
}
public static void main(String[] args) {
MaxPathSum solution = new MaxPathSum();
// 构造一棵二叉树(示例)
TreeNode root = new TreeNode(10);
root.left = new TreeNode(2);
root.right = new TreeNode(10);
root.left.left = new TreeNode(20);
root.left.right = new TreeNode(-15);
root.right.right = new TreeNode(20);
root.left.left.left = new TreeNode(-20);
root.right.right.left = new TreeNode(3);
root.right.right.right = new TreeNode(-4);
int result = solution.maxPathSum(root);
System.out.println("最大路径和: " + result);
}
}
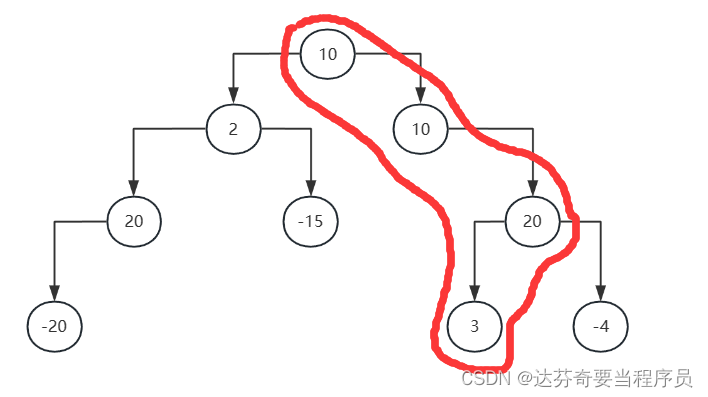
这个实现中,maxPathSum 方法返回的是以当前节点为根的最大路径和。在递归的过程中,不断更新 maxSum 变量,最终得到整棵树的最大路径和。