二叉树遍历
基本介绍:
二叉树主要有两种遍历方式:
- 深度优先遍历:先往深走,遇到叶子节点再往回走。【前中后序遍历】
- 广度优先遍历:一层一层的去遍历。【层序遍历】
这两种遍历是图论中最基本的两种遍历方式
- 深度优先遍历
- 前序遍历(递归法,迭代法)
- 中序遍历(递归法,迭代法)
- 后序遍历(递归法,迭代法)
- 广度优先遍历
- 层次遍历(迭代法)
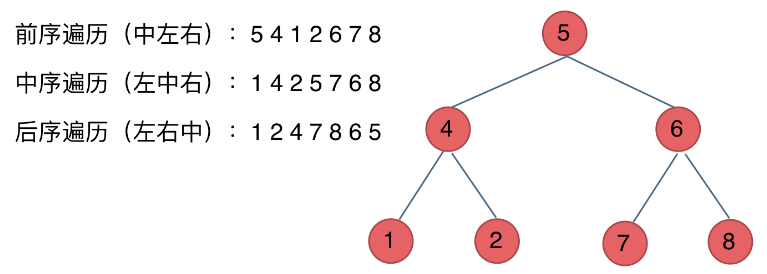
前中后序遍历,这里前中后,其实指的就是根节点的遍历顺序
前序遍历:根左右
中序遍历:左根右
后序遍历:左右根
看如下例子:
栈其实就是递归的一种是实现结构,也就说前中后序遍历的逻辑其实都是可以借助栈使用非递归的方式来实现的。
二叉树定义:
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
二叉树深度优先遍历(前中后序):
二叉树递归遍历:
递归算法的三个要素。每次写递归,都按照这三要素来写,可以保证大家写出正确的递归算法!
- 确定递归函数的参数和返回值: 确定哪些参数是递归的过程中需要处理的,那么就在递归函数里加上这个参数, 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
- 确定终止条件: 写完了递归算法, 运行的时候,经常会遇到栈溢出的错误,就是没写终止条件或者终止条件写的不对,操作系统也是用一个栈的结构来保存每一层递归的信息,如果递归没有终止,操作系统的内存栈必然就会溢出。
- 确定单层递归的逻辑: 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。
下面以前序遍历为例:
其他两种遍历修改递归代码顺序即可。
前序:
class Solution {
List<Integer> ans = new ArrayList<>(); //返回值
public List<Integer> preorderTraversal(TreeNode root) { //参数
//递归出口
if(root == null){
return ans;
}
//下面就是递归逻辑
//根
ans.add(root.val);
//左
if(root.left != null) preorderTraversal(root.left);
//右
if(root.right != null) preorderTraversal(root.right);
return ans;
}
}
二叉树迭代遍历:
递归遍历需要借助栈这种数据结构了,以前序遍历为例,直接从根节点开始,一直向左节点遍历直到左节点为空将节点压入栈中,此时压栈顺序就是我们要的顺序根左,压栈的同时将结果放入List中,此时进行出栈回溯操作,当前节点置为栈顶节点的右孩子然后继续从当前节点继续上述压栈操作,这才实现真正意义上的根左右,具体代码如下:
前序迭代:
public List<Integer> preorderTraversal(TreeNode root) {
//迭代法
List<Integer> ans = new ArrayList<>();
if(root == null){
return ans;
}
Stack<TreeNode> stack = new Stack<>();
while(root != null || !stack.isEmpty()){
while(root != null){
//这个顺序就是我们要的
ans.add(root.val); //根左
//将根节点和左节点压栈
stack.push(root);
root = root.left;
}
//出栈回溯
//继续将栈顶元素的右孩子的左孩子继续压栈
TreeNode node = stack.pop();
root = node.right; //右
}
return ans;
}
中序迭代:
中序迭代相当于上述前序迭代,仅仅改变一行代码顺序即可,前序是入栈就是我们要的顺序根左,现在中序是左根,所以将出栈元素顺序放入结果即可,代码如下。
public List<Integer> inorderTraversal(TreeNode root) {
//迭代法
List<Integer> ans = new ArrayList<>();
if(root == null){
return ans;
}
Stack<TreeNode> stack = new Stack<>();
while(root != null || !stack.isEmpty()){
while(root != null){
//将根节点和左节点压栈
stack.push(root);
root = root.left;
}
//出栈回溯
//继续将栈顶元素的右孩子的左孩子继续压栈
TreeNode node = stack.pop();
ans.add(node.val); //左根
root = node.right; //右
}
return ans;
}
后序迭代:
最后的后序遍历就不能单纯的改变代码顺序就能实现了,后序遍历顺序是左右根,我们可以先得到根右左的顺序,最后将结果反转就得到目标结果,代码如下:
public List<Integer> postorderTraversal(TreeNode root) {
//迭代法
List<Integer> ans = new ArrayList<>();
if(root == null){
return ans;
}
Stack<TreeNode> stack = new Stack<>();
while(root != null || !stack.isEmpty()){
while(root != null){
ans.add(root.val); //根右
//将根节点和右节点压栈
stack.push(root);
root = root.right;
}
//出栈回溯
//继续将栈顶元素的左孩子的右孩子继续压栈
TreeNode node = stack.pop();
root = node.left; //左
}
//最后将结果反转即可
Collections.reverse(ans);
return ans;
}
二叉树广度优先遍历(层序):
层序遍历需要借助队列这种数据结构了,每层遍历的顺序满足队列先将进先出的特点。
我们需要一个队列以及需要一个变量记录每层节点的个数,每一层节点出队列时,需要将该节点的左右子孩子加入队列中。
实际效果如下:

具体代码如下:
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> ans = new ArrayList<>();
if (root == null) {
return ans;
}
Queue<TreeNode> queue = new ArrayDeque<>();
queue.offer(root);
while (!queue.isEmpty()) {
//记录每一层节点个数
int size = queue.size();
List<Integer> temp = new ArrayList<>();
//一边将该层节点出队列,一边将节点的左右子节点加入队列,直到最后队列为空结束循环
while (size > 0) {
TreeNode node = queue.poll();
temp.add(node.val);
//将该节点的左右子节点放入队列
if (node.left != null) queue.offer(node.left);
if (node.right != null) queue.offer(node.right);
size--;
}
ans.add(temp);
}
return ans;
}
深度优先遍历需要用到栈这种数据结构,广度优先遍历借助队列这种数据结构。
104.二叉树的最大深度
力扣题目链接
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
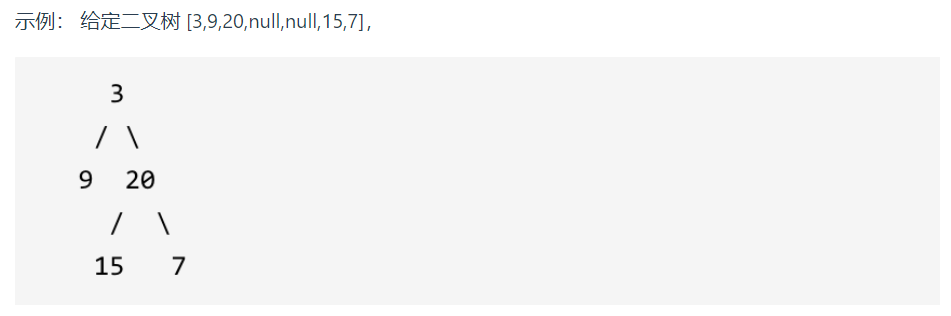
返回它的最大深度 3 。
递归法
找出左右子树最大深度 + 1返回
递归三部曲
1、递归参数和返回值
参数就是树的根节点,返回值即树的高度,代码如下:
public int getDepth(TreeNode root)
2、递归出口
如果根节点为空,直接返回高度0
if(root == null) return 0;
3、递归逻辑
递归左子树、右子树得到左右子树高度,得到最大值 + 1返回
//左节点
int leftDepth = getDepth(root.left);
//右节点
int rightDepth = getDepth(root.right);
//根节点
return Math.max(leftDepth, rightDepth) + 1;
上述代码类似后序遍历。
完整递归代码
class Solution {
public int maxDepth(TreeNode root) {
return getDepth(root);
}
public int getDepth(TreeNode root){
if(root == null) return 0;
//左子树
int leftDepth = getDepth(root.left);
//右子树
int rightDepth = getDepth(root.right);
//根节点
return Math.max(leftDepth, rightDepth) + 1;
}
}
迭代法——广度优先遍历
层序遍历记录树的深度
public int maxDepth(TreeNode root) {
if(root == null) return 0;
int depth = 0;
Queue<TreeNode> queue = new ArrayDeque<>();
queue.offer(root);
while(!queue.isEmpty()){
//每一层节点个数
int size = queue.size();
depth++;
for(int i = 0; i < size; i++){
TreeNode node = queue.poll();
if(node.left != null) queue.offer(node.left);
if(node.right != null) queue.offer(node.right);
}
}
return depth;
}
111.二叉树的最小深度
力扣题目链接
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。

返回它的最小深度 2 。
思路
二叉树的最小深度,即当一个节点没有左右孩子(叶子节点)时,此时的深度就是最小深度。
迭代法——广度优先遍历
public int minDepth(TreeNode root) {
//层序遍历
if(root == null) return 0;
Queue<TreeNode> queue = new ArrayDeque<>();
queue.offer(root);
int depth = 0;
while(!queue.isEmpty()){
int size = queue.size();
depth++;
for(int i = 0; i < size; i++){
TreeNode node = queue.poll();
//某个节点的左右子孩子都为空,此时的深度就是最小深度
if(node.left == null && node.right == null){
return depth;
}
if(node.left != null) queue.offer(node.left);
if(node.right != null) queue.offer(node.right);
}
}
return depth;
}
递归法见代码随想录
226.翻转二叉树
力扣题目链接
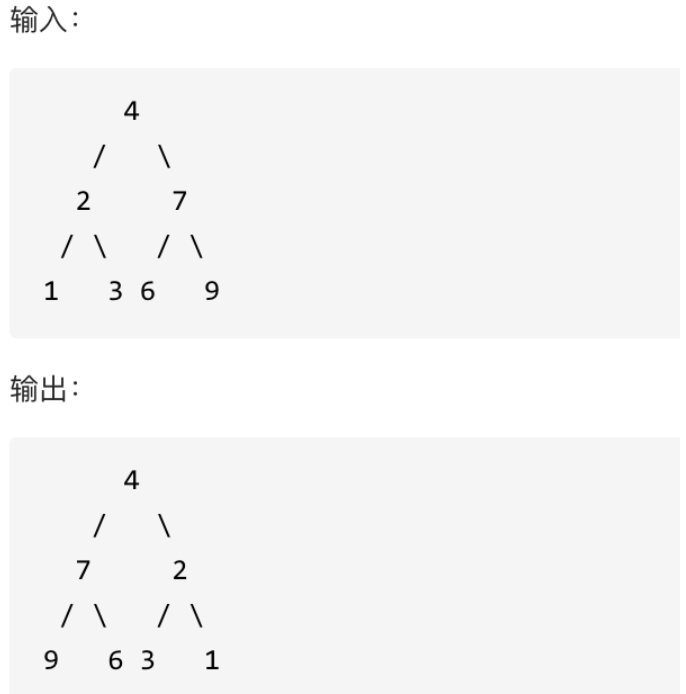
翻转一棵二叉树。
示例:
思路
该题只需将每一个节点的左右孩子节点交换即可。
递归法
public TreeNode invertTree(TreeNode root){
//递归出口
if(root == null){
return root;
}
//交换节点的左右孩子节点
swap(root);
//递归左子树
invertTree(root.left);
//递归右子树
invertTree(root.right);
return root;
}
/**
* 交换该节点的左右孩子节点
*/
public void swap(TreeNode node){
TreeNode temp = node.left;
node.left = node.right;
node.right = temp;
}
迭代法
借助栈/队列来遍历树,进而交换每个节点的左右孩子节点
借助队列
public TreeNode invertTree(TreeNode root){
//迭代法
//交换每个节点的左右孩子即可
if(root == null) return root;
Queue<TreeNode> queue = new ArrayDeque<>();
queue.offer(root);
while(!queue.isEmpty()){
TreeNode node = queue.poll();
swap(node);
if(node.left != null) queue.offer(node.left);
if(node.right != null) queue.offer(node.right);
}
return root;
}
借助栈
public TreeNode invertTree(TreeNode root){
//迭代法
//交换每个节点的左右孩子即可
if(root == null) return root;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while(!stack.isEmpty()){
TreeNode node = stack.pop();
swap(node);
if(node.left != null) stack.push(node.left);
if(node.right != null) stack.push(node.right);
}
return root;
}
101. 对称二叉树
力扣题目链接
给定一个二叉树,检查它是否是镜像对称的。

思路:
首先要明确,判断二叉树是否是对称二叉树,要比较的不是左右节点!
对于二叉树是否对称,要比较的是根节点的左子树与右子树是不是相互翻转的,理解这一点就知道了其实我们要比较的是两个树(这两个树是根节点的左右子树),所以在递归遍历的过程中,也是要同时遍历两棵树。【判断根节点的左右子树的内侧和外侧节点是否是都相同】
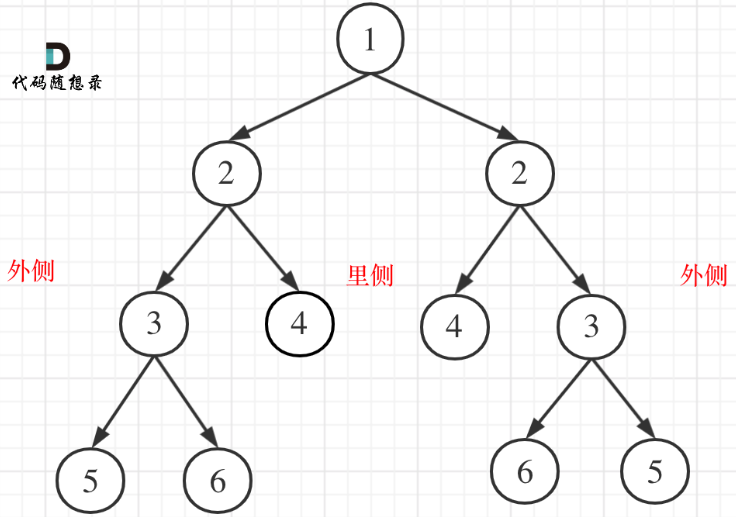
递归法
1、确定递归函数的参数和返回值
因为我们要比较的是根节点的两个子树是否是相互翻转的,进而判断这个树是不是对称树,所以要比较的是两个树,参数自然也是左子树节点和右子树节点。
返回值自然是boolean类型。
代码如下:
boolean compare(TreeNode left, TreeNode right)
2、确定终止条件
要比较两个节点数值相不相同,首先要把两个节点为空的情况弄清楚!否则后面比较数值的时候就会操作空指针了。
节点为空的情况有:(注意我们比较的其实不是左孩子和右孩子,所以如下我称之为左节点右节点)
- 左节点为空,右节点不为空,不对称,return false
- 左不为空,右为空,不对称 return false
- 左右都为空,对称,返回true
- 左右节点值不相等,返回false
- 最后左右节点的值相等,继续递归判断对应内侧节点、各外侧节点是否都相等
代码如下:
if(left == null && right != null){ // 左空右不空
return false;
}else if(left != null && right == null){ // 左不空右空
return false;
}else if(left == null && right == null){ //左右都空
return true;
}else if(left.val != right.val){ // 左右值不相等
return false;
}
最后是else if不是else,就是因为还有上述最后一种情况左右节点的值都相等还需要继续递归。
3、单层递归的逻辑
此时才进入单层递归的逻辑,单层递归的逻辑就是处理 左右节点都不为空,且数值相同的情况。
- 比较二叉树外侧是否对称:传入的是左节点的左孩子,右节点的右孩子。
- 比较内测是否对称,传入左节点的右孩子,右节点的左孩子。
- 如果左右都对称就返回true ,有一侧不对称就返回false 。
代码如下:
//左右值相等 继续递归 左子树外侧和右子树外侧、左子树内侧以及右子树内侧
boolean outside = compare(left.left, right.right);
boolean inside = compare(left.right, right.left);
//两棵树的内外侧都相等返回true
return inside && outside;
最后完整递归代码如下:
class Solution {
public boolean isSymmetric(TreeNode root) {
return compare(root.left, root.right);
}
//递归,判断根节点的左右子树的外侧和内测是否都相等
public boolean compare(TreeNode left, TreeNode right){
if(left == null && right != null){ // 左空右不空
return false;
}else if(left != null && right == null){ // 左不空右空
return false;
}else if(left == null && right == null){ //左右都空
return true;
}else if(left.val != right.val){ // 左右值不相等
return false;
}
//左右值相等 继续递归 左子树外侧和右子树外侧、左子树内侧以及右子树内侧
boolean outside = compare(left.left, right.right);
boolean inside = compare(left.right, right.left);
//两棵树的内外侧都相等返回true
return inside && outside;
}
}
迭代法
使用队列
我们可以借助队列来判断左右子树,左子树->左右,右子树->右左,对于节点元素是否相等来判断该树是否是对称二叉树。

代码如下:
如下的条件判断和递归的逻辑是一样的。
class Solution {
public boolean isSymmetric(TreeNode root) {
Deque<TreeNode> queue = new LinkedList<>();
//将左右子树根节点放入队列中
queue.offer(root.left);
queue.offer(root.right);
while(!queue.isEmpty()){
//取出左右子树对应顺序的节点
TreeNode left = queue.pop();
TreeNode right = queue.pop();
//左右两节点都为空,继续判断
if(left == null && right == null){
continue; // !!!为什么是continue?而不是直接返回false?
}
if(left == null && right != null){
return false;
}else if(left != null && right == null){
return false;
}else if(left.val != right.val){
return false;
}
queue.offer(left.left);//左子树外侧
queue.offer(right.right);//右子树外侧
queue.offer(left.right);//左子树内侧
queue.offer(right.left);//右子树内侧
}
return true;
}
}
//左右两节点都为空,继续判断
if(left == null && right == null){
continue; // !!!为什么是continue?而不是直接返回false?
}
如上一段代码,是为什么呢?看如下例子:
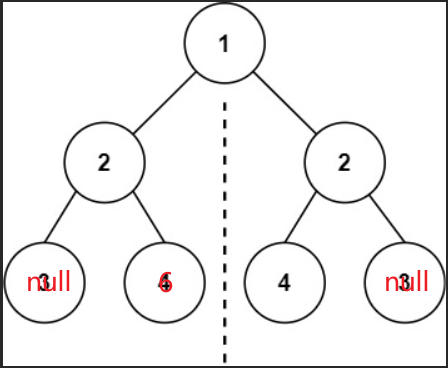
当判断左右子树对应的第一个外侧节点时,此时对应两个节点都为null,如果直接返回true判断有误,所以应该跳过该节点继续判断后续节点,所以应该是continue而不是直接返回true
使用栈
细心的话,其实可以发现,这个迭代法,其实是把左右两个子树要比较的元素顺序放进一个容器,然后成对成对的取出来进行比较,那么其实使用栈也是可以的。
只要把队列原封不动的改成栈就可以了,代码如下。
class Solution {
public boolean isSymmetric(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
//先将左右子树对应根节点放入栈中
stack.push(root.left);
stack.push(root.right);
while(!stack.isEmpty()){
//取出左右子树对应顺序的节点
TreeNode left = stack.pop();
TreeNode right = stack.pop();
//左右两节点都为空,继续判断
if(left == null && right == null){
continue;
}
if(left == null && right != null){
return false;
}else if(left != null && right == null){
return false;
}else if(left.val != right.val){
return false;
}
stack.push(left.left);//左子树外侧
stack.push(right.right);//右子树外侧
stack.push(left.right);//左子树内侧
stack.push(right.left);//右子树内侧
}
return true;
}
}
257. 二叉树的所有路径
力扣题目链接
给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。
示例:

思路
前序遍历递归+回溯
如下图:
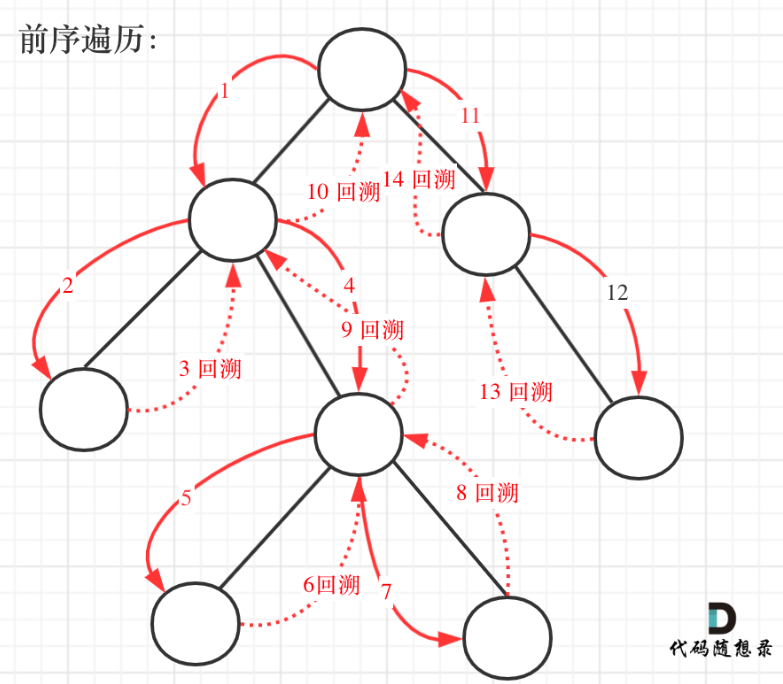
class Solution {
List<String> ans = new ArrayList<>();
List<Integer> list = new ArrayList();
public List<String> binaryTreePaths(TreeNode root) {
if(root == null){
return ans;
}
list.add(root.val);
if(root.left != null){
binaryTreePaths(root.left);
//回溯
list.remove(list.size() - 1);
}
if(root.right != null) {
binaryTreePaths(root.right);
//回溯
list.remove(list.size() - 1);
}
//叶子节点
if(root.left == null && root.right == null){
ans.add(getPath(list));
}
return ans;
}
public String getPath(List<Integer> list){
StringBuilder sb = new StringBuilder();
for(int i = 0; i < list.size(); i++){
if(i == list.size() - 1){
sb.append(list.get(i));
}else
sb.append(list.get(i)).append("->");
}
return sb.toString();
}
}
或者
class Solution {
public List<String> binaryTreePaths(TreeNode root) {
List<String> ans = new ArrayList<>();
if(root == null){
return ans;
}
dfs(root, "", ans);
return ans;
}
/**
* 深度优先遍历
*/
public void dfs(TreeNode node, String path, List<String> ans){
if(node == null){
return;
}
path += node.val;
//根节点
if(node.left == null && node.right == null){
ans.add(path);
} else{
//不是根节点继续递归
path += "->";
dfs(node.left, path, ans);
dfs(node.right, path, ans);
}
}
}
106.从中序与后序遍历序列构造二叉树
力扣题目链接
根据一棵树的中序遍历与后序遍历构造二叉树。
注意: 你可以假设树中没有重复的元素。
例如,给出
中序遍历 inorder = [9,3,15,20,7] ;后序遍历 postorder = [9,15,7,20,3]
返回如下的二叉树:

代码及实现步骤:
public class LC106 {
/**
* 哈希表快速查找,元素索引 用于查找中序数组中根节点索引下标
*/
Map<Integer, Integer> map;
/*
整体步骤:
1、第一步根据后序数组每次都能得到树的根节点
2、得到根节点后,在中序数组中找到根节点下标索引,切割中序数组,该索引左边就是左子树节点,右边就是右子树节点
3、然后根据左子树长度,可以从后序数组也切割出对应左子树节点和右子树节点
4、在根据中序、后序数组对应左右子树节点递归得到对应左右孩子节点
5、没有必要每次都创建新的数组再做处理,可以直接给出前后索引范围在原数组上直接切割处理,可以节省不少空间
*/
public TreeNode buildTree(int[] inorder, int[] postorder) {
map = new HashMap<>();
for (int i = 0; i < inorder.length; i++) {
map.put(inorder[i], i);
}
return buildNode(inorder, 0, inorder.length, postorder, 0, postorder.length);
}
public TreeNode buildNode(int[] inorder, int inBegin, int inEnd, int[] postorder, int postBegin, int postEnd) {
// 参数下标遵循左闭右开原则
if (inBegin >= inEnd || postBegin >= postEnd) {
// 不满足条件,数组中没有元素直接返回
return null;
}
// 后序数组最后一个元素是根节点元素
// 从中序数组中得到根节点下标索引
int rootIndex = map.get(postorder[postEnd - 1]);
// 创建节点
TreeNode root = new TreeNode(postorder[postEnd - 1]);
// 保存中序左子树个数,用来确定后序数列的个数
int lenOfLeft = rootIndex - inBegin;
// 递归构建左右子树 中序左数组&后序左数组
root.left = buildNode(inorder, inBegin, rootIndex, postorder, postBegin, postBegin + lenOfLeft);
// 中序右数组&后序右数组
root.right = buildNode(inorder, rootIndex + 1, inEnd, postorder, postBegin + lenOfLeft, postEnd - 1);
return root;
}
}
二叉树其余题目见代码随想录