目录
一、二分查找的基本原理
二、二分查找的基本写法
三、二分查找的相关例题
1. LeetCode704.二分查找
2. LeetCode35.搜索插入位置
3. LeetCode34.在排序数组中查找的第一个和最后一个位置
4. LeetCode69.x的平方根
5. LeetCode367.有效的完全平方数
一、二分查找的基本原理
二分查找又称折半查找,意指将待查找的集合通过判定某种条件将该集合一分为二,即左区间和右区间,两个区间只有一个区间是满足该条件的,再次判定该条件,再次划分,直到区间划分完毕。下面看动图演示
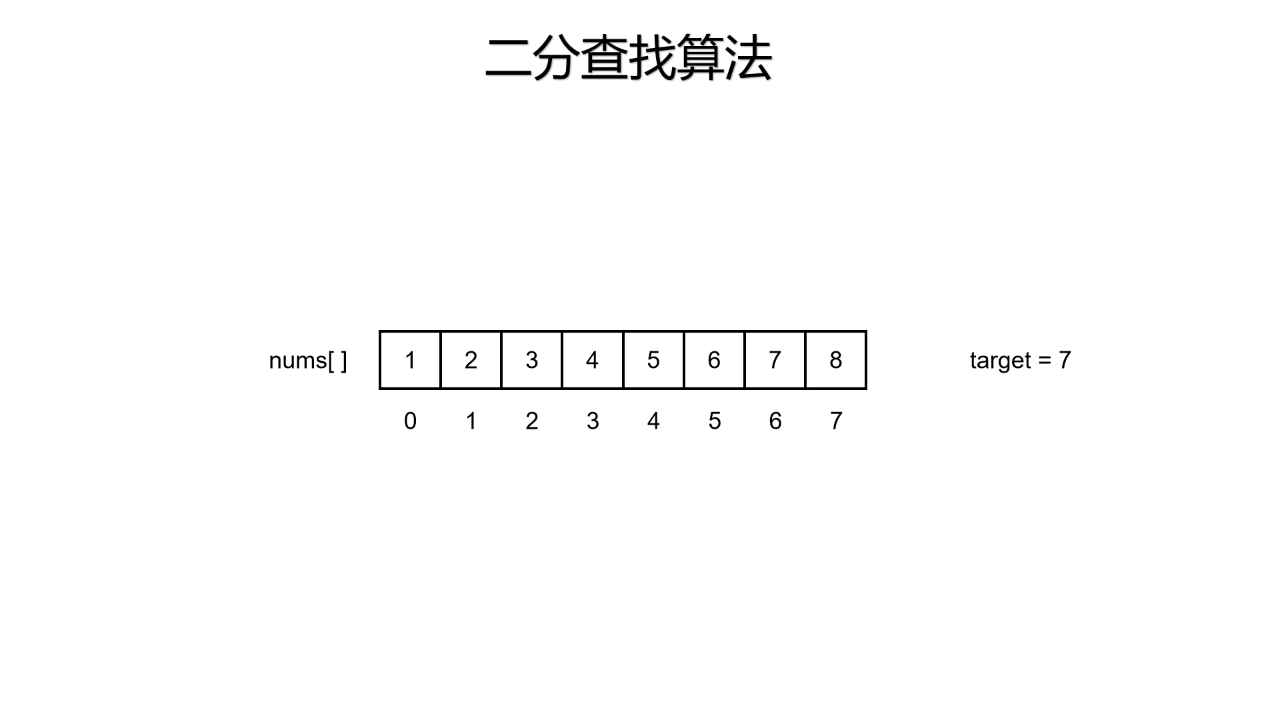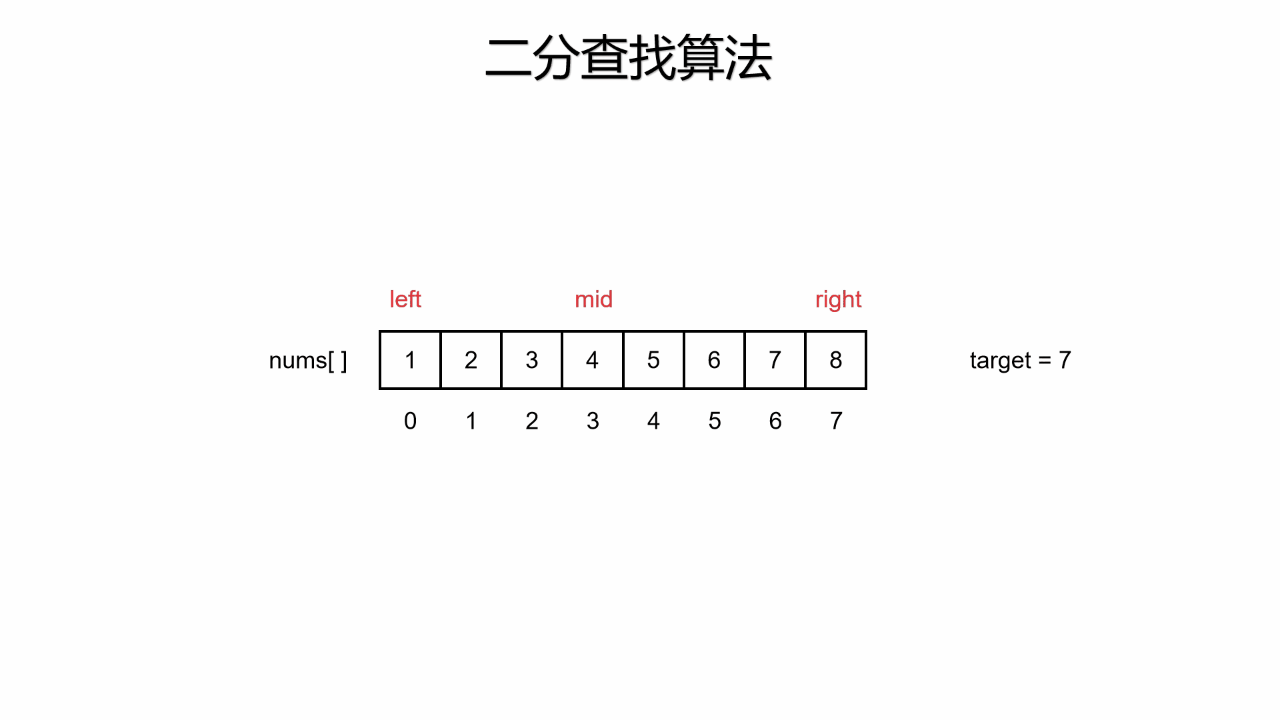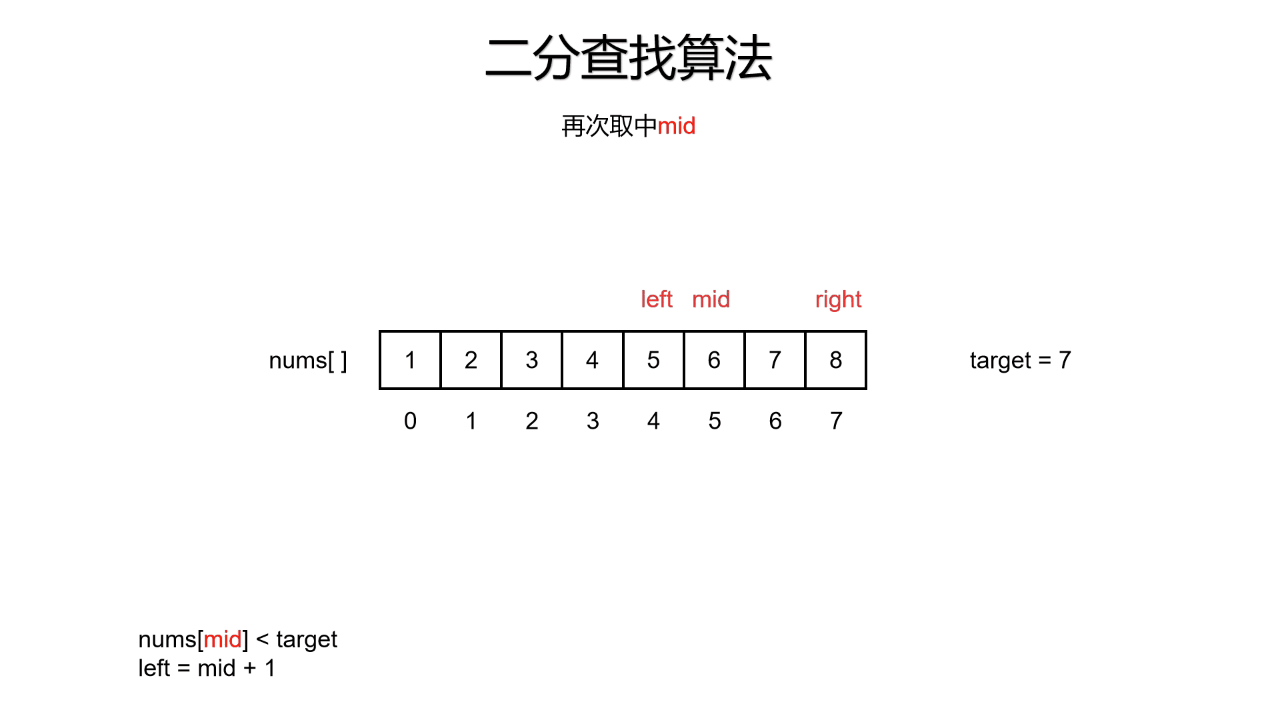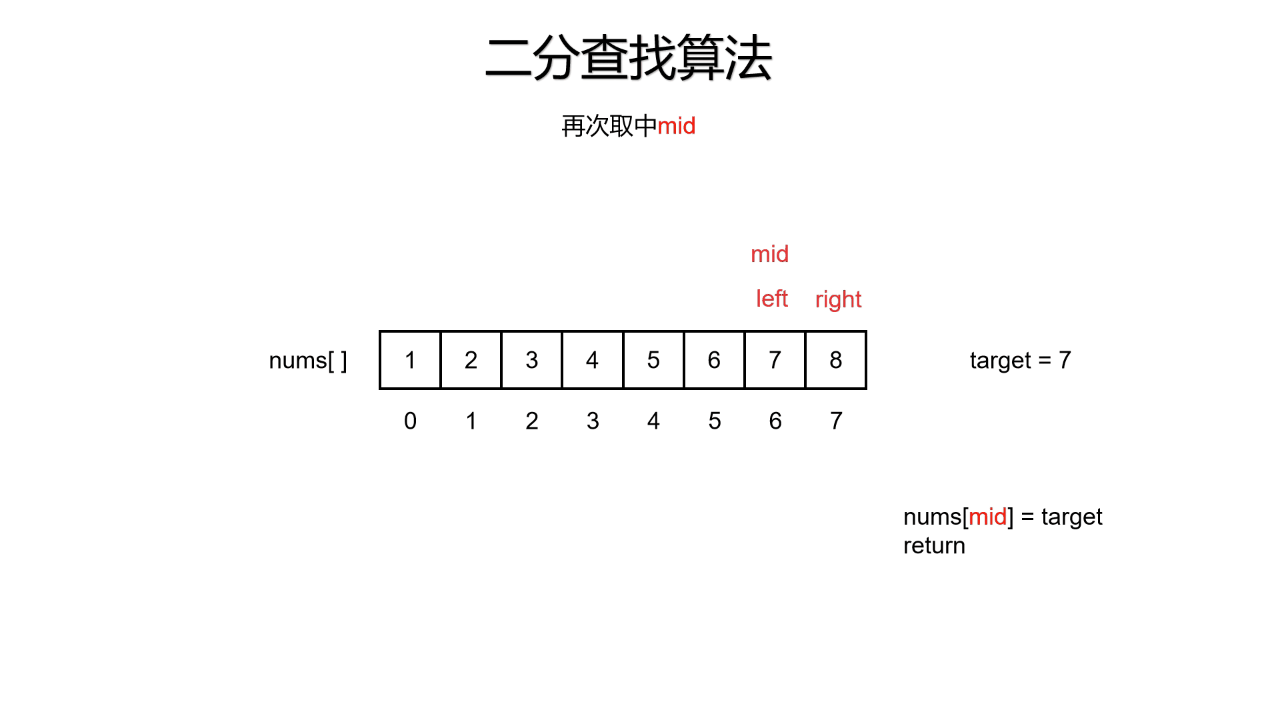
二、二分查找的基本写法
写法一:
// 版本一
class Solution {
public:
int binary_search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]
while (left <= right)
{
int mid = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
if (nums[mid] > target)
{
right = mid - 1; // target 在左区间,所以[left, mid - 1]
}
else if (nums[mid] < target)
{
left = mid + 1; // target 在右区间,所以[mid + 1, right]
}
else // nums[mid] == target
{
return mid; // 数组中找到目标值,直接返回下标
}
}
return -1;// 未找到目标值
}
};
写法二:
// 版本二
class Solution {
public:
int binary_search(vector<int>& nums, int target)
{
int left = 0;
int right = nums.size(); // 定义target在左闭右开的区间里,即:[left, right)
while (left < right)
{
int mid = left + ((right - left) >> 1);
if (nums[mid] > target)
{
right = mid; // target 在左区间,在[left, mid)中
}
else if (nums[mid] < target)
{
left = mid + 1; // target 在右区间,在[mid + 1, right)中
}
else // nums[mid] == target
{
return mid; // 数组中找到目标值,直接返回下标
}
}
return -1;// 未找到目标值
}
};三、二分查找的相关例题
1. LeetCode704.二分查找
链接:二分查找

题解:
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size();
while(left < right)
{
int mid = (left + right) / 2;
if(nums[mid] > target)
{
right = mid;
}
else if(nums[mid] < target)
{
left = mid + 1;
}
else
{
return mid;
}
}
return -1;
}
};2. LeetCode35.搜索插入位置
链接:搜索插入位置
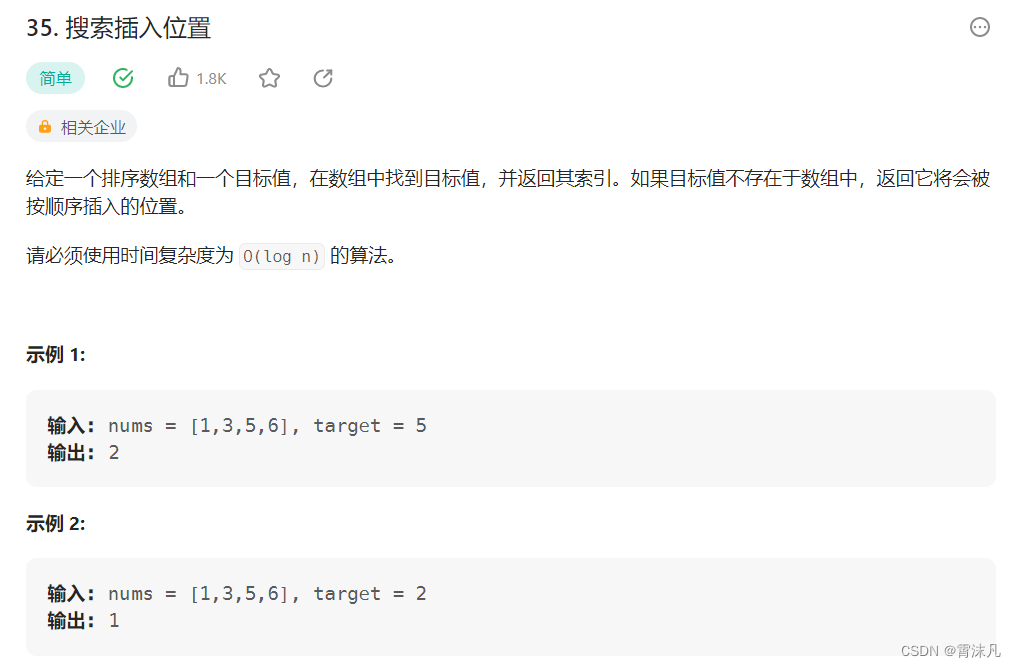
题解:

对于第三次二分后,我们发现left、right和mid同时指向了数组中的最后一个元素;
这种情况只要是target不存在,一定会走到这一步。
此时又会分两种情况:
- 当target > nums[mid] 时:right = mid - 1,此时二分结束,right的下标是-1,left的下标是0;
- 当target < nums[mid] 时:left = mid + 1,此时二分结束,right的下标是0,left的下标是1;
我们一定是将target插入到right和left之间,如何插入正确的下标中:
- 首先,left、right和mid是同一个下标;
- left = mid + 1表明target比mid下标对应的值要大;left++的这个位置就是该target所在位置,或者right+1;因为right和left是连续的下标。
- right = mid - 1表明target比mid下标对应的值要小;right + 1这个位置就是该target所在位置,或者left;因为right和left是连续的下。
- 这两种情况,都是一样的,就合成一种情况了。
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1;
while(left <= right)
{
int mid = (left + right) / 2;
if(nums[mid] < target)
{
left = mid + 1;
}
else if(nums[mid] > target)
{
right = mid - 1;
}
else
{
return mid;
}
}
return left;//return right + 1;
}
};3. LeetCode34.在排序数组中查找的第一个和最后一个位置
链接:在排序数组中查找的第一个和最后一个位置

题解1:
寻找target在数组里的左右边界,有如下三种情况:
- 情况一:target 在数组范围的右边或者左边,例如数组{3, 4, 5},target为2或者数组{3, 4, 5},target为6,此时应该返回{-1, -1}
- 情况二:target 在数组范围中,且数组中不存在target,例如数组{3,6,7},target为5,此时应该返回{-1, -1}
- 情况三:target 在数组范围中,且数组中存在target,例如数组{3,6,7},target为6,此时应该返回{1, 1}
如何找左右边界:
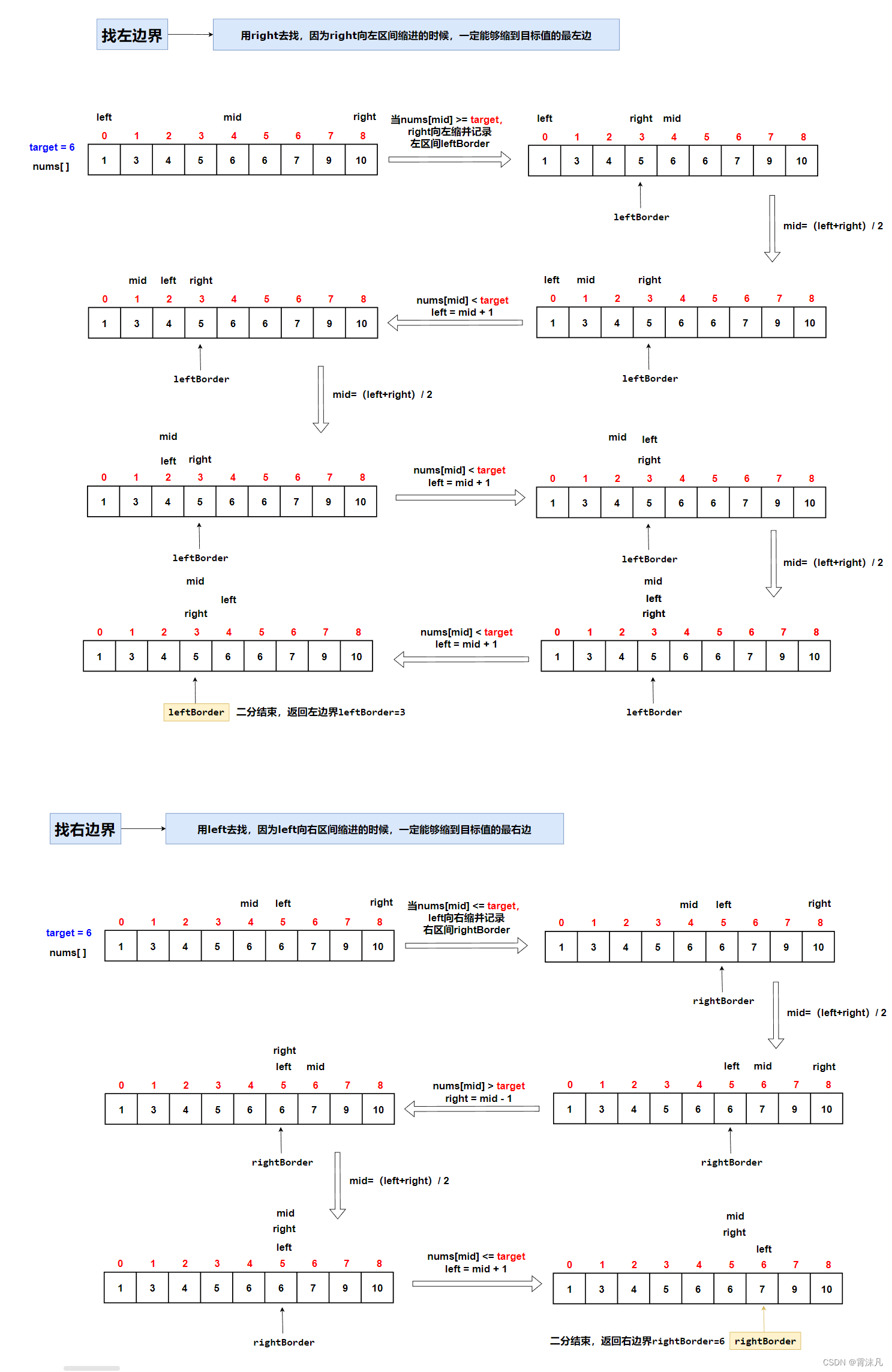
从图中给的例子来看,target=6 的区间是[4, 5],但是我们的leftBorder和rightBorder是[3,6],没关系,我们只需要在后续处理中将leftBorder+1和rightBorder-1即可;下面看代码:
class Solution {
private:
int GetLeftBorder(vector<int>& nums, int target)
{
int left = 0;
int right = nums.size() - 1;
int leftBorder = -2;//定义左区间,这是用来判断有没有被赋值过
//为什么给-2,因为right在向左区间移动时,最坏移动到下标 -1 的位置
while(left <= right)
{
int mid = (left + right) / 2;
if(nums[mid] >= target)//此时区间被划分为[left, mid - 1]
{
right = mid - 1;
leftBorder = right;//有可能nums[mid] == target,记录target的左开区间
}
else//此时区间被划分为[mid + 1, right]
{
left = mid + 1;
}
}
return leftBorder;
}
int GetRightBorder(vector<int>& nums, int target)
{
int left = 0;
int right = nums.size() - 1;
int rightBorder = -2;//定义左区间,这是用来判断有没有被赋值过
while(left <= right)
{
int mid = (left + right) / 2;
if(nums[mid] > target)//此时区间被划分为[left, mid - 1]
{
right = mid - 1;
}
else//此时区间被划分为[mid + 1, right]
{
left = mid + 1;
rightBorder = left;//有可能nums[mid] == target,记录target的右开区间
}
}
return rightBorder;
}
public:
vector<int> searchRange(vector<int>& nums, int target) {
int leftBorder = GetLeftBorder(nums, target);
int rightBorder = GetRightBorder(nums, target);
//情况1:
if(leftBorder == -2 || rightBorder == -2) return {-1, -1};
//情况3:因为是两个记录的都是开区间,只要相减大于1,必然target存在于数组中,将leftBorder + 1和rightBorder - 1
if(rightBorder - leftBorder > 1) return {leftBorder + 1, rightBorder - 1};
//情况2:
return {-1, -1};
}
};4. LeetCode69.x的平方根
链接: x的平方根
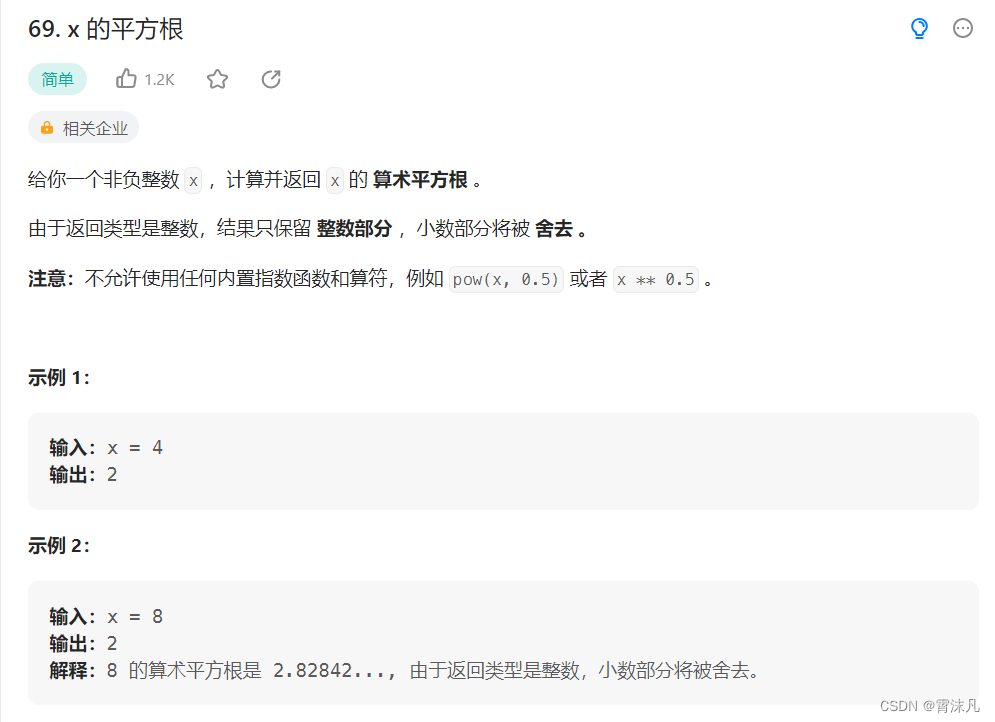
题解:
class Solution {
public:
int mySqrt(int x) {
double left = 0;
double right = x;
while((right - left) > 1e-8)
{
double mid = (left + right) / 2;
if(mid * mid >= x)
{
right = mid;
}
else
{
left = mid;
}
}
return right;
}
};5. LeetCode367.有效的完全平方数
链接:有效的平方数
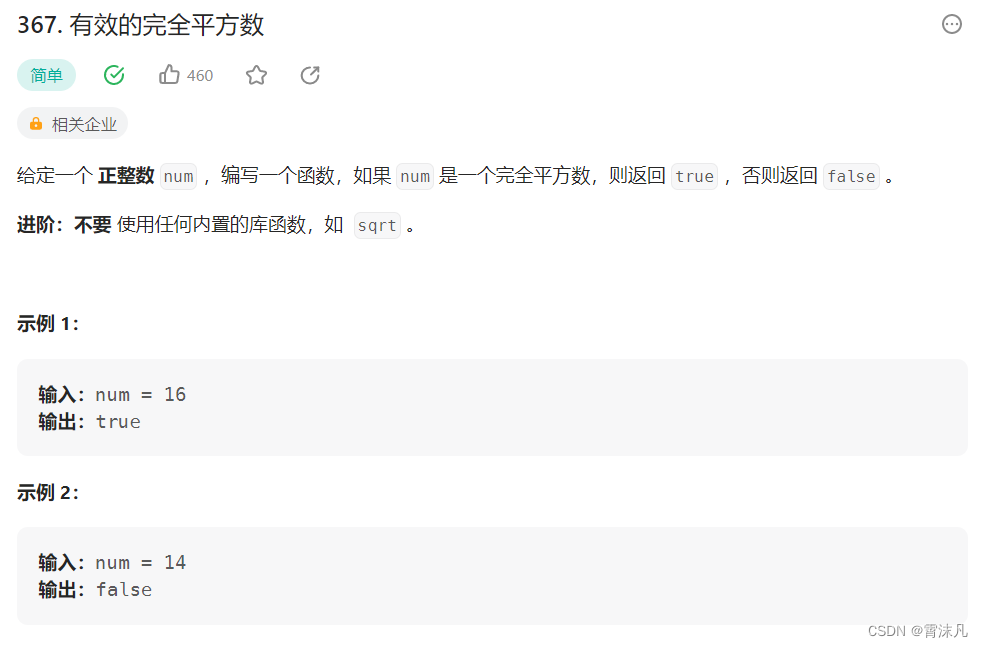
题解:这道题相对来说简单一些;
class Solution {
public:
bool isPerfectSquare(int num) {
//如果num有完全平方数,那么完全平方数一定在0~num中
int left = 0,right = num;
while(left <= right)
{
int mid = (left + right) / 2;
long square = (long)mid * mid;
if(square < num)//表明mid < num,区间变为[mid + 1,right]
{
left = mid + 1;
}
else if(square > num)//表明mid > num,区间变为[left,mid + 1]
{
right = mid - 1;
}
else //square == num,表明mid就是要找的完全平方数
{
return true;
}
}
return false;
}
};







![【LeetCode】验证二叉搜索树 [M]](https://img-blog.csdnimg.cn/img_convert/a7488a34e4b7e3b7fda2f1e8aff17a99.jpeg)