目录

简介

AES的加密过程如下（以128位密钥为例）：

异或运算

初始变换（initial round）

字节代换（SubBytes）

行位移（ShiftRows）

列混合（MixColumns）

轮密钥加（AddRoundKey）

---

简介

        AES高级加密标准（Advanced Encryption Standard）  对称加密，分组（128bit）加密，128bit的密钥，密钥长度也可以是192位或256位 但是对应的加密轮数不同。        

        由于DES已经被破解，其脆弱性也随着时间的推移不断显现，AES的出现旨在取代DES成为广泛使用的标准。虽然来自微软和比利时鲁汶天主教大学(欧洲顶级高校)的研究人员们近日就发现了一种可以攻破AES的方法。这种新型攻击方法破解AES密钥所需的时间只有此前方法的三分之一到五分之一，而且对任何版本的AES加密算法都适用。AES算法的发明人Joan Daemen、Vincent Rijmen也都已经证明了上述攻击的有效性，但是目前没有人能完整的破解AES。

AES	加密密钥长度 （32位比特字)	明文分组长度(32位比特字)	加密轮数
AES-128	4	4	10
AES-192	6	4	12
AES-256	8	4	14

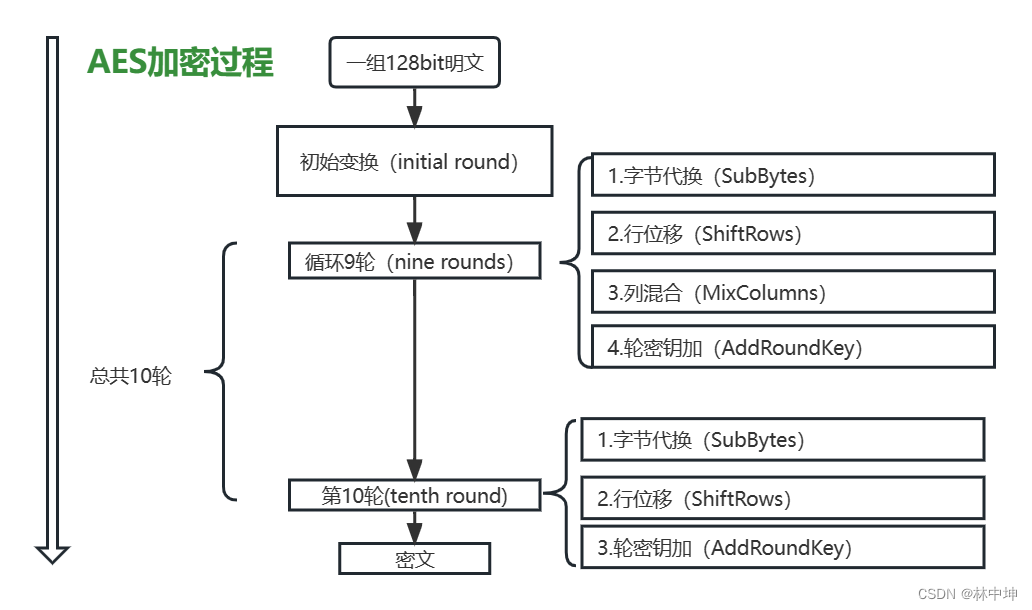
 AES的整体加密过程如下，具体每一步的详细过程我将依次讲述：

运算单位：DES作为64位加密密钥，以位为加密单位，横向排列，AES是以字节为加密单位，纵向排列，但是最终的运算都是以二进制为单位。

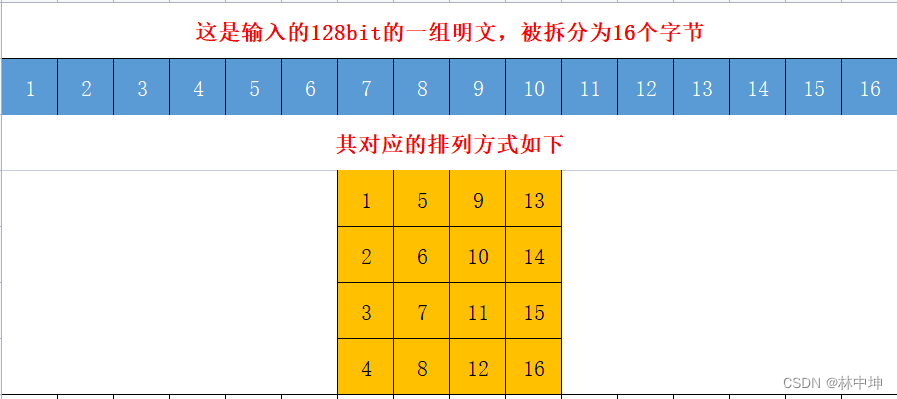
AES的加密过程如下（以128位密钥为例）：

异或运算

        所谓异或运算就是将两组二进制序列按位进行比较，同取0，异取1的过程

举例： 1 0 0 1和0 1 0 1

        1 0 0 1

        0 1 0 1

结果为：1 1 0 0

初始变换（initial round）

        初始变换就是将明文矩阵和第0轮的key密钥按字节进行异或运算的过程，此过程得到的最终矩阵将进行十轮运算。

举例：

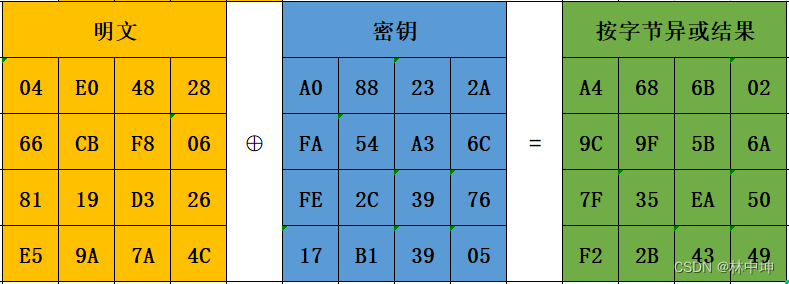
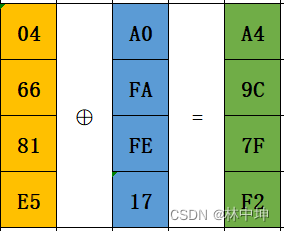
04对应的二进制为：0 0 0 0 0 1 0 0

A0对应的二进制为：1 0 1 0 0 0 0 0

二者异或结果为：1 0 1 0 0 0 1 0 0等于A4

字节代换（SubBytes）

        字节代换就是查表，每个字节的前1个值就是行数，后1个值就是列数

在S-Box表中找到对应行列位置的值，替换这个值即可。

举例：2D对应2行，D列，就将D8这个值替换到这个位置。

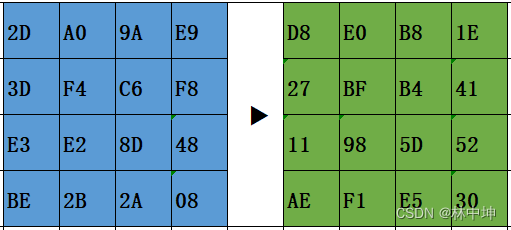
S-Box表如下

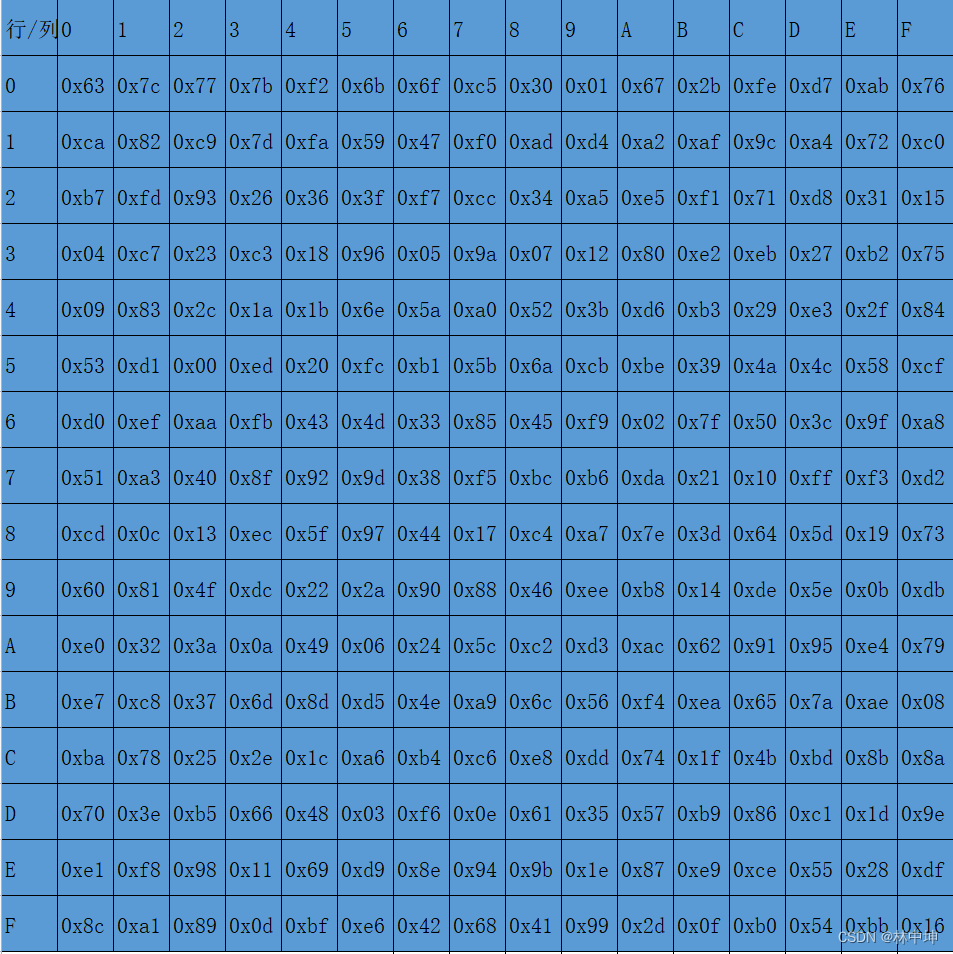
行位移（ShiftRows）

        行的位移其实就是每一行左移指定个字节，移出去的字节补在本行最后。具体如下，由于比较好理解就不举例了。

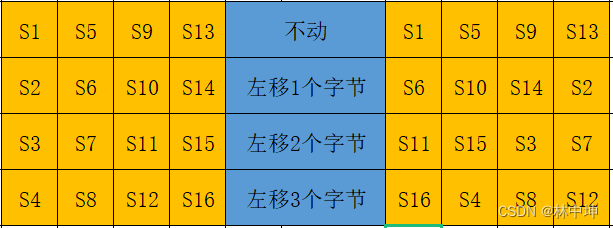
列混合（MixColumns）

        经过行位移之后的矩阵叫状态矩阵S，列混合就是把该矩阵左乘一个固定矩阵，该矩阵只有三种数值（01，02，03）。

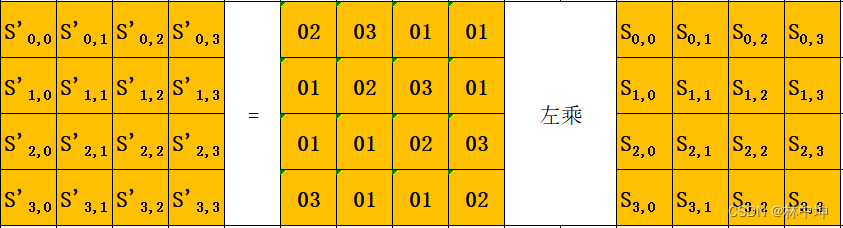
        这里的左乘不是普通数学意义上的乘积，也不是简单的线性代数那样的矩阵相乘，它基于GF(2^8)上的二元运算，具体我没研究过，反正就按照以下公式来算就行。

每个位置的值运算规则为

                                

计算公式如下：

00000010对应02，00000011对应03 00000001对应01

a7a6a5a4a3a2a1a0对应某一个字节的8位

 

 

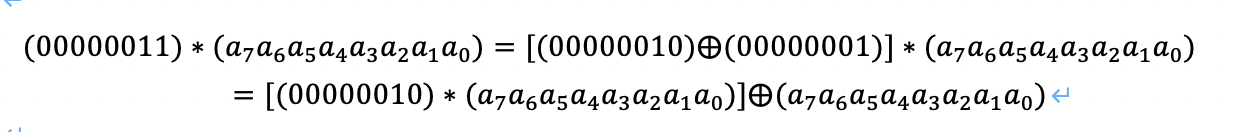
以S举例：

 

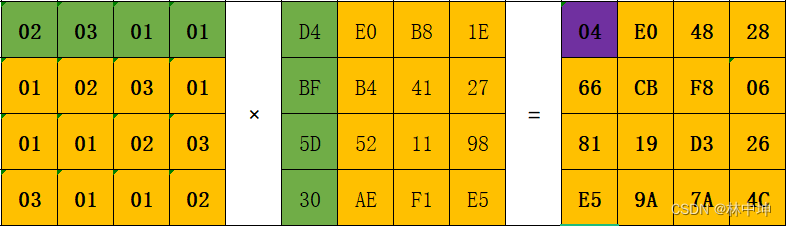
轮密钥加（AddRoundKey）

        首先，将初始密钥放在一个4X4的矩阵，如下图

情况1：如果i不是4的倍数，那么第i列由如下等式确定：W[ i ] = W[ i-4 ] ⨁ W[ i-1 ]

        例如W[ 5 ]的计算如下：

                W[ 5 ]= W[ 1 ]⨁W[ 4 ]

                                                   

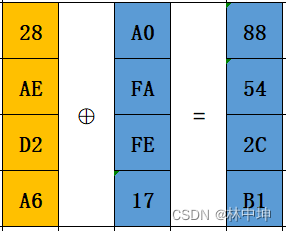
情况2：如果i是4的倍数，那么第i列由如下等式确定：W[i] = W[ i-4 ] ⨁ T(W[ i-1 ])

  T（）函数又分为三步：字循环，字节代换和轮常量异或

第一步：字循环：将1个字中的4个字节循环左移1个字节。即将输入字[b0, b1, b2, b3]变换成[b1,b2,b3,b0]。
第二步：字节代换：对字循环的结果使用S盒进行字节代换。
第三步：轮常量异或：将前两步的结果同轮常量Rcon[j]进行异或，其中j表示轮数。

举例：

         W[ 4 ]= W[ 0 ] ⨁ T(W[ 3 ])

T函数运算如下：

第一步：字循环

第二步：字节代换，参照S-Box表进行代换

第三步：轮常量异或

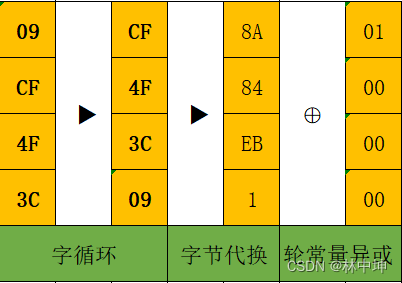
最后这个轮常量异或有个对应的表，一共十组

所以   W[ 4 ]= W[ 0 ] ⨁ T(W[ 3 ])

              

 

 到此为止AES的加密过程学习完毕，若有错误欢迎指正！