前言

Manacher算法是一种回文串查找算法，专门用于处理查找字符串中的回文子串操作。
虽然这个算法本身只是用于查找回文子串，但是它的查找思想还是非常值得学习的。
由于Manacher算法是基于暴力解法优化而来的，所以在阅读正式的算法之前，需要先了解暴力解法的思路和过程。
leetcode指路：最长回文子串

一、暴力解法

1.重构字符串

这里我们采取从中间向两边扩散的方式，动态查找可能存在的最大回文串。
例如以0下标位置的为中心的最长回文子串为a

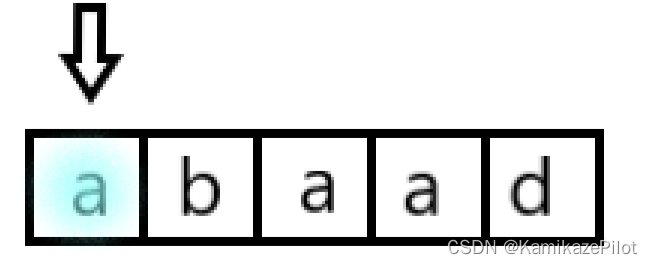
以1下标位置的为中心的最长回文子串为aba

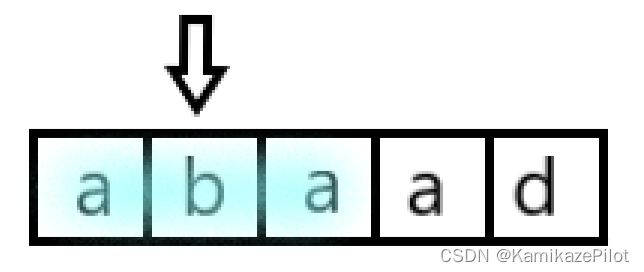
以2下标位置的为中心的最长回文子串为a
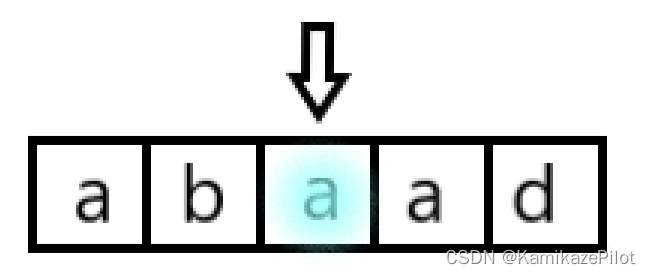
但是这种求解过程有一定局限性，它无法判断长度为偶数的回文串
所以如果我们需要同时判断偶数个的子串，就需要从两个值之间的位置出发判断
这里的选择，是通过直接添加补间字符的方式来解决这个问题。
例如：

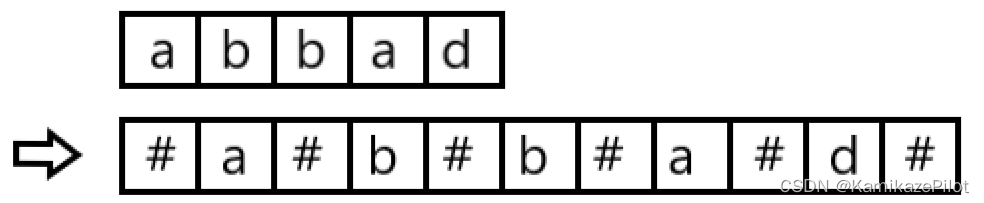
这样的话我们就可以判断偶数串的回文情况。
至于为何前后各额外添加了一个#，则是为了后面方便计算使用。
重构字符串代码：

	static void manacherString(const string& str, string& s)
	{
		s.clear();
		s.reserve(str.size() * 2 + 1);
		s.push_back('#');
		for (char c : str)
		{
			s.push_back(c);
			s.push_back('#');
		}
	}

2.暴力解法

依然是遍历字符串，从每个位置开始向两边扩展来找到最大的回文子串，即while循环中的逻辑
其中while循环的判断条件是查看是否越界，if语句用于判断边界上的两个字符是否相等。
这里首先定义一个当前半径r，然后进入while循环，只要while循环不跳出，半径就自增，通过这种方式来查找最大半径。（0位置不用看，自己和自己必定相等）
又因为我们这里查找的是已经重构了的字符串，所以此时 真实的子串长度 == 重构子串长度 - 1，这也是返回时，返回maxValue - 1 的原因

	static int maxLcpsLength(const string& str)
	{
		if (str.empty()) return 0;
		string mStr;
		manacherString(str, mStr);
		int maxValue = 0;
		for (int i = 0; i < mStr.size(); i++)
		{
			int r = 1;
			// 找到以i 为中点的最大回文子串
			while (i + r < mStr.size() && i - r > -1)
			{
				// 不相等就跳出
				if (mStr[i + r] != mStr[i - r]) break;
				//相等就扩大
				r++;
			}
			// 更新最大值
			maxValue = max(r, maxValue);
		}
		return maxValue - 1;
	}

这个方法还是相对而言比较简单的，而Manacher就是在这个解法上进行优化，过滤了很多重复计算过的优化算法

二、`Manacher`算法

有了以上的知识作为基础，我们在来说Manacher算法的原理，它其实是一种动态规划的思想

将之前所求得的所有最大回文子串半径存在一个辅助数组中，并应用到之后的求解过程中
要如何应用我们已知的回文串信息呢？
这里需要记录两个关键信息：已知最远右边界R，已知最远右边界中心点C。
例如下图中：如果当指针遍历过C点时，发现它的回文半径可以衍生到R位置，是目前遍历过的里面最远的，那么就更新C和R的信息，直到发现更远的边界下标为止。
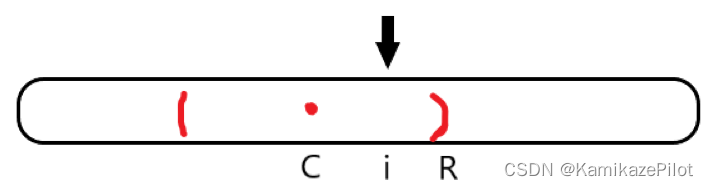
假设我们有i'关于中心点C与当前位置i对称
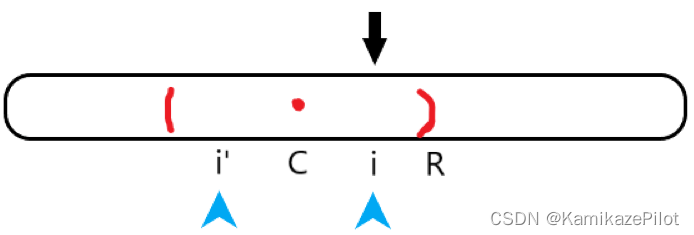
首先我们已经求解过i'位置的回文信息
先说结论：i'位置上的最大回文子串半径可以帮助我们过滤一定的特殊情况运算
当i在R范围以内时，我们可以利用已知的回文串对称的性质，将i在R范围以内的运算全部过滤掉.
之后的情况可以分为几种情况讨论

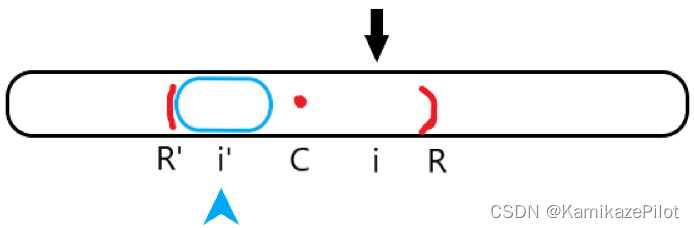
i位置越过了R边界范围，此时i'也在R'范围之外
i位置没有越过R边界范围时，若i'位置的最大回文子串在已知最远回文串以内，即i'位置最大回文串左边界大于R'
i位置没有越过R边界范围时，若i'位置的最大回文子串在已知最远回文串边界上，即i'位置最大回文串左边界等于R'
i位置没有越过R边界范围时，若i'位置的最大回文子串越过了已知最远回文串，即i'位置最大回文串左边界小于R'

第一种情况是不可避免运算的，此时已有的信息不能帮助我们进行下一步的运算，此时需要暴力求解i位置的最大回文串
第二种情况下，因为i'在R' ~ R以内，且边界不在R'上，所以i'最大回文串两边的元素一定不相等，且这两个元素都在R' ~ R以内，由此可得，i的最大回文串一定与i'的最大回文串相等。
第三种情况下，由于边界有交集，所以无法证明R范围以外不存在以i为中心，更大的回文串。这种情况下，可以过滤半径在R' ~ R范围以内的运算
第四种情况下，已知i'最大回文串越界，又由于R' ~ R范围两边的元素一定不相等，所以i'的最大回文串在R'范围外的元素与i在R界外的元素一定不相等，所以这种情况下R' ~ R范围外也不存在以i位置为中心更大的回文串。

由于上述分析可得：我们最多可以过滤的运算数量有3种情况

过滤不了，暴力扩
过滤i'个
过滤R - i个，即i' - R'个

基于上述理论，我们可以对之前的算法进行优化，下面给出代码

三、完整代码

class Solution
{
	static void manacherString(const string& str, string& s)
	{
		s.clear();
		s.reserve(str.size() * 2 + 1);
		s.push_back('#');
		for (char c : str)
		{
			s.push_back(c);
			s.push_back('#');
		}
	}
public:
	static int maxLcpsLength(const string& str)
	{
		if (str.empty()) return 0;
		string mStr;
		// 重构字符串
		manacherString(str, mStr);
		int* mArr = new int[mStr.size()];
		for_each(mArr, mArr + mStr.size(), [](int ele) { ele = 0; });	
		int C = -1;
		int R = -1;
		int max = 0;
		for (int i = 0; i < mStr.size(); i++)
		{
			// 找到可以跳过的扩充区间
			mArr[i] = R > i ? min(mArr[2 * C - i], R - i) : 1;
			// 找到以i 为中点的最大回文子串
			while (i + mArr[i] < mStr.size() && i - mArr[i] > -1 
				&& mStr[i + mArr[i]] == mStr[i - mArr[i]])
			{
				//相等就扩大
				mArr[i]++;
			}
			// 更新最大边界
			if (i + mArr[i] > R)
			{
				R = i + mArr[i];
				C = i;
			}
			// 更新最大值（也可以值即记录值）
			max = mArr[max] > mArr[i] ? max : i;
		}
		return mArr[max] - 1;
	}

};