꒰˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱
ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客
本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN 如需转载还请通知˶⍤⃝˶
个人主页:xiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客
系列专栏:xiaoxie的算法系列专栏——CSDN博客●'ᴗ'σσணღ*
我的目标:"团团等我💪( ◡̀_◡́ ҂)"( ⸝⸝⸝›ᴥ‹⸝⸝⸝ )欢迎各位→点赞👍 + 收藏⭐️ + 留言📝+关注(互三必回)!
目录
一.二分查找
1.说明
2.二分查找的模板
1.普通二分查找模板:
2.寻找左边界的二分查找模板
3. 寻找右边界的二分查找模板
4. 二分查找变体模板1(寻找第一个满足条件的值):
5. 二分查找变体模板2(寻找最后一个满足条件的值):
6. 旋转数组的二分查找模板:
3.红蓝二分查找法
1.

一.二分查找
1.说明
相信有很多读者都认为二分查找法就是一个非常简单的算法,没有什么技术含量,博主想说的是二分查找本身的思想确实十分简单,当它奇妙的就是在它的边界确定条件上,相信大家在写二分查找的时候经常在边境确定的时候出现问题导致结果出现误差。
2.二分查找的模板
此外,目前二分查找主流的有六套模板。博主把它们归纳总结了一下
1.普通二分查找模板:
public int binarySearch(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
return mid; // 找到目标值,返回索引
} else if (nums[mid] < target) {
left = mid + 1; // 目标值在右半部分
} else {
right = mid - 1; // 目标值在左半部分
}
}
return -1; // 未找到目标值
}
2.寻找左边界的二分查找模板
public int leftBound(int[] nums, int target) {
int left = 0, right = nums.length;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1; // 目标值在右半部分
} else {
right = mid; // 目标值在左半部分
}
}
return left; // 返回左边界索引
}
3. 寻找右边界的二分查找模板
public int rightBound(int[] nums, int target) {
int left = 0, right = nums.length;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] <= target) {
left = mid + 1; // 目标值在右半部分
} else {
right = mid; // 目标值在左半部分
}
}
return left - 1; // 返回右边界索引
}
4. 二分查找变体模板1(寻找第一个满足条件的值):
public int firstPosition(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1; // 目标值在右半部分
} else {
right = mid; // 目标值在左半部分
}
}
return nums[left] == target ? left : -1; // 返回第一个满足条件的值的索引
}
5. 二分查找变体模板2(寻找最后一个满足条件的值):
public int lastPosition(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left < right) {
int mid = left + (right - left + 1) / 2;
if (nums[mid] > target) {
right = mid - 1; // 目标值在左半部分
} else {
left = mid; // 目标值在右半部分
}
}
return nums[left] == target ? left : -1; // 返回最后一个满足条件的值的索引
}
6. 旋转数组的二分查找模板:
public int searchRotated(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
return mid; // 找到目标值,返回索引
}
if (nums[left] <= nums[mid]) {
if (nums[left] <= target && target < nums[mid]) {
right = mid - 1; // 目标值在左半部分
} else {
left = mid + 1; // 目标值在右半部分
}
} else {
if (nums[mid] < target && target <= nums[right]) {
left = mid + 1; // 目标值在右半部分
} else {
right = mid - 1; // 目标值在左半部分
}
}
}
return -1; // 未找到目标值
}
以上就是目前主流的一些二分查找的模板,当然如果大家对二分查找有着深刻了解,也可以自己创建出一些二分查找的模板,只有你能理解二分法这一思想,再加上对边界的判断我相信你对二分查找法应该没什么问题
3.红蓝二分查找法
1. 说明
博主介绍的红蓝二分查找法和普通二分查找法不同的是
这套模板和常规的模板存在不一样: 主体思路:L 指针掌管左边蓝色区域, R指针掌管右边红色区域,两者互不冲突,通过不断向目标元素靠近扩大掌管区域,直到两者掌管区域接壤,即 l+1==r 时终止。
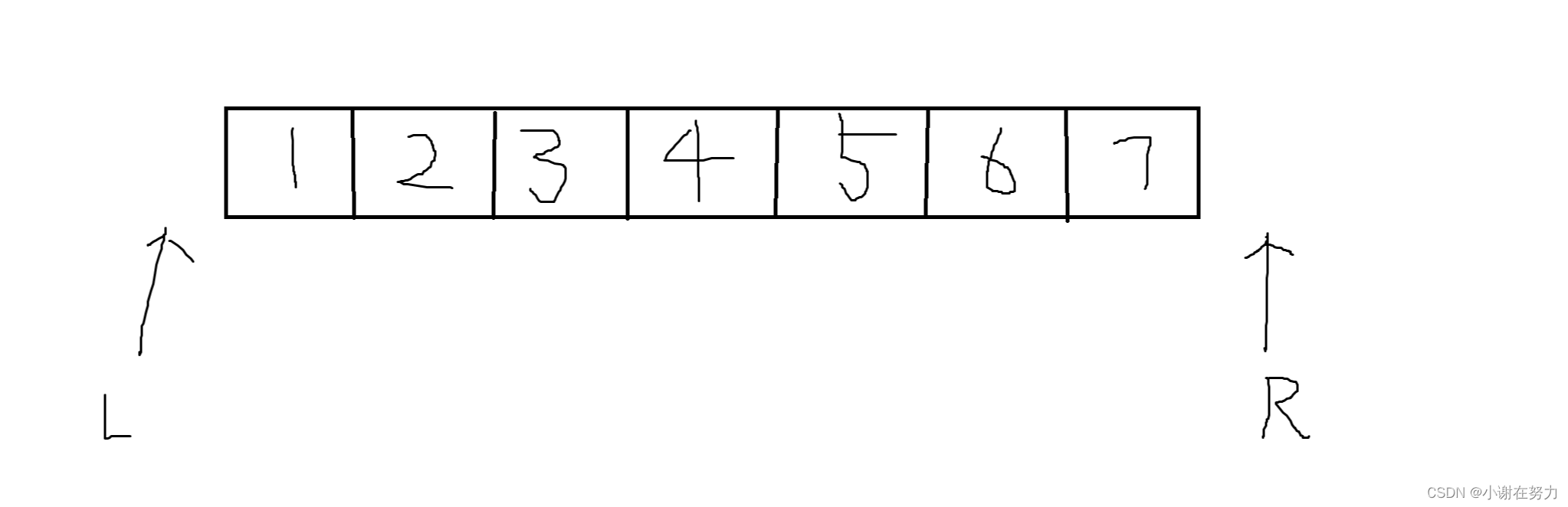
2.模板
//简代码
int L = 0;
int R = nums.length;
while(L+1 < R) {
int M = (L+R)/2//如果数字大时可以使用 M = L +(R-L)/2;
if (isblue(m)) {
L = M;
} else {
R = M ;
}
} return L/R //根据实际情况情况选择 3.详细讲解
开始时,L指针和 R指针取在搜索区间界外,L=首个元素下标−1,R=末尾元素下标+1,此时所有元素均未着色;
循环条件始终为 L+1 < R,当 L=R 时跳出循环,此时蓝红区域划分完成,所有元素均已着色;
M指针取值始终为 M =(L+R)/2
L指针和 R指针变化的时候直接变为 M指针,即对 M 指针所指向元素进行染色,无需 +1 或者−1;
本模板唯一变化的地方是判断目标元素最终落在左边蓝色区域还是右边红色区域。以不变应万变,根据情况的不同,变换判断条件,大大的降低了出错的可能。以下还有一些我们需要注意到的说明
1.根据target的情况 < 、≤在左边蓝色区域找,≥ 、>在右边红色区域找
2.染色完成后的特殊情况:如果遍历完成后都为蓝色区域的话左边红色区域长度为 0 ,如果搜索目标位于左边红色区域,则搜索结果不存在,同理都为红色区域右边蓝色区域长度为 0 ,如果搜索目标位于右边蓝色区域,则搜索结果不存在一般需要后期处理。
3.普通技巧: 以下技巧必须掌握: 排序 二分查找的运用是建立在数组有序的基础上的,如果数组无序,我们要先对数组进行排序,如果数组有多个维度,我们针对需要二分查找的维度进行排序。 构造二分查找区间 当问题能够转化为区间内二分判定问题的时候,构造搜索区间,在蓝红二分法中设L指针初始为L0;R指针设为二分查找结束后L指针始终为Lt,R指针始终为Rt,target在(Lt--Rt)之间双指针 L 和 R 始终对目标元素 targettargettarget 进行夹逼,这是一条非常重要的性质。 如果开始构造搜索区间没有思路的时候,直接用题目提示中的数值区间!如果开始构造搜索区间没有思路的时候,直接用题目提示中的数值区间!
4. 高阶技巧: 缩进边界构造区间 在第④条中,我们讨论了全蓝或者全红的特殊状态,其实我们可以提前判断,根据题意:
搜索区间第一个元素颜色待定,搜索区间最后一个元素颜色待定,L=首个元素下标−1,R=末尾元素下标+1,如区间为[0, n−1]则L=-1,R=N;
搜索区间第一个元素最终一定为蓝色,搜索区间最后一个元素颜色待定,L=首个元素下标,R=末尾元素下标+1,如区间为[0, n−1]则L=0,R=N;
搜索区间第一个元素颜色待定,搜索区间最后一个元素最终一定为红色L=首个元素下标−1,R=末尾元素下标,如区间为[0, n−1]则L=-1,R=N-1;
搜索区间第一个元素最终一定为蓝色,搜索区间最后一个元素一定为红色L=首个元素下标−1,R=末尾元素下标+1,如区间为[0, n−1]则L=-1,R=N;
4.实战演示
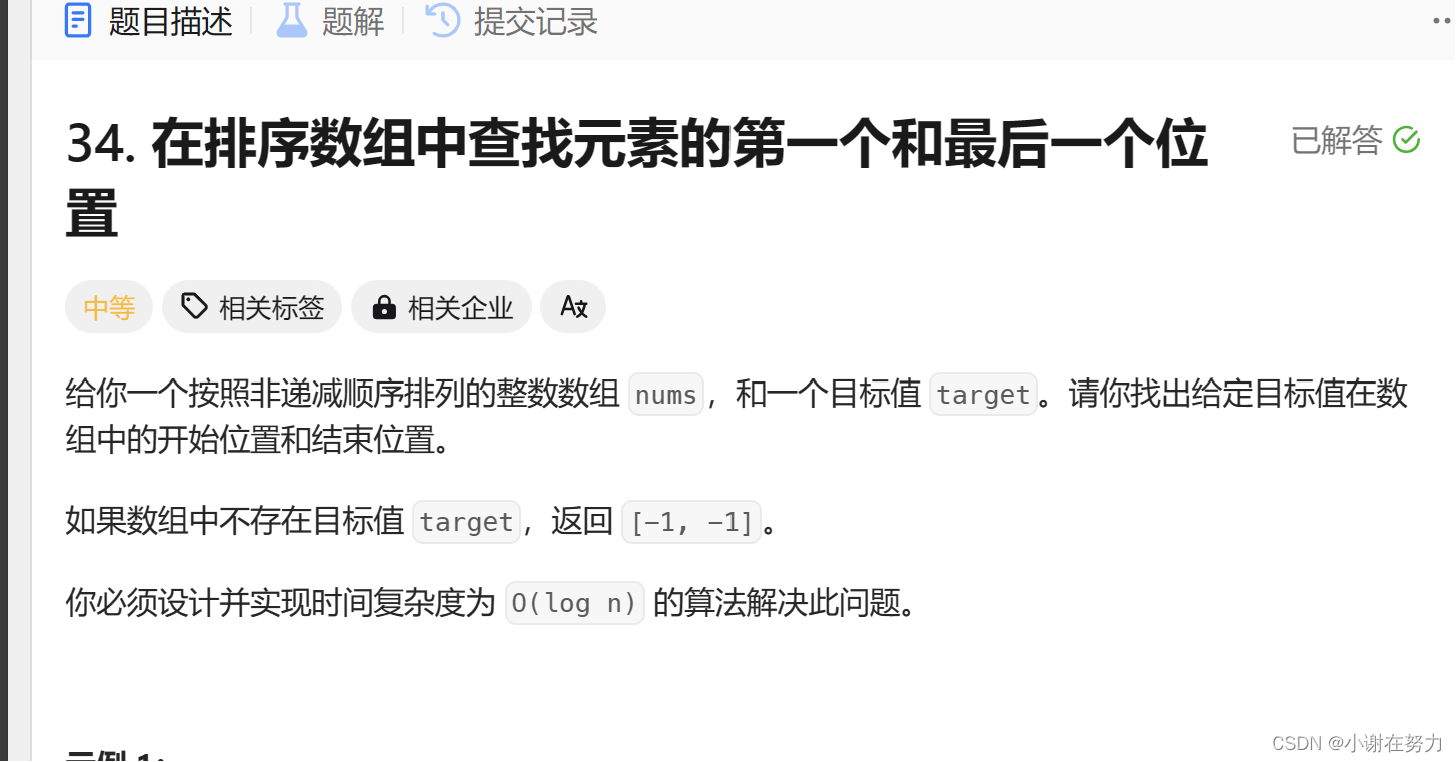
如力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
class Solution {
public int searchRangeLeft(int[] nums, int target) {
int left = -1;
int right =nums.length;
while (left+1 != right) {
int mid = (left + right) / 2;
if(nums[mid] <= target) {
left = mid;
}else {
right = mid;
}
}
return left;
}
public int searchRangeRight(int[] nums, int target) {
int left = -1;
int right =nums.length;
while (left+1 != right) {
int mid = (left + right) / 2;
if(nums[mid] < target) {
left = mid;
}else {
right = mid;
}
}
return right;
}
public int[] searchRange(int[] nums, int target) {
int leftIndex = searchRangeLeft(nums,target);
int rightIndex = searchRangeRight(nums,target);
if(leftIndex >= rightIndex && leftIndex < nums.length && nums[leftIndex] == target && nums[rightIndex] == target) {
return new int[] {rightIndex,leftIndex};
}
return new int[] {-1,-1};
}
}以上就是我使用该模板的解决的一道题,读者有兴趣也可以去尝试一下,链接如下
34. 在排序数组中查找元素的第一个和最后一个位置
以上就是关于蓝红二分查找法的模板和内容了,当然如果你比较熟悉二分查找法的思想也可以自己做一个模板。