❤ 作者主页：欢迎来到我的技术博客😎
❀ 个人介绍：大家好，本人热衷于Java后端开发，欢迎来交流学习哦！(￣▽￣)~*
🍊 如果文章对您有帮助，记得关注、点赞、收藏、评论⭐️⭐️⭐️
📣 您的支持将是我创作的动力，让我们一起加油进步吧！！！🎉🎉

一、两数之和

1. 题目描述

---

2. 思路分析

最容易想到的方法是枚举数组中的每一个数 $x$，寻找数组中是否存在 $target-x$。

使用哈希表，可以将寻找 $target-x$ 的时间复杂度降低到从 $O(N)$ 降低到 $O(1)$。

循环一遍nums数组，在每步循环中做两件事：
1、判断 target - nums[i] 是否出现在哈希表中;
2、将 nums[i] 插入到哈希表中。

---

3. 代码实现

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> heap;
        for (int i = 0; i < nums.size(); i ++) {
            int r = target - nums[i];
            if (heap.count(r)) return {heap[r], i};
            heap[nums[i]] = i;
        }
        return {};
    }
};

---

二、两数相加

1. 题目描述

---

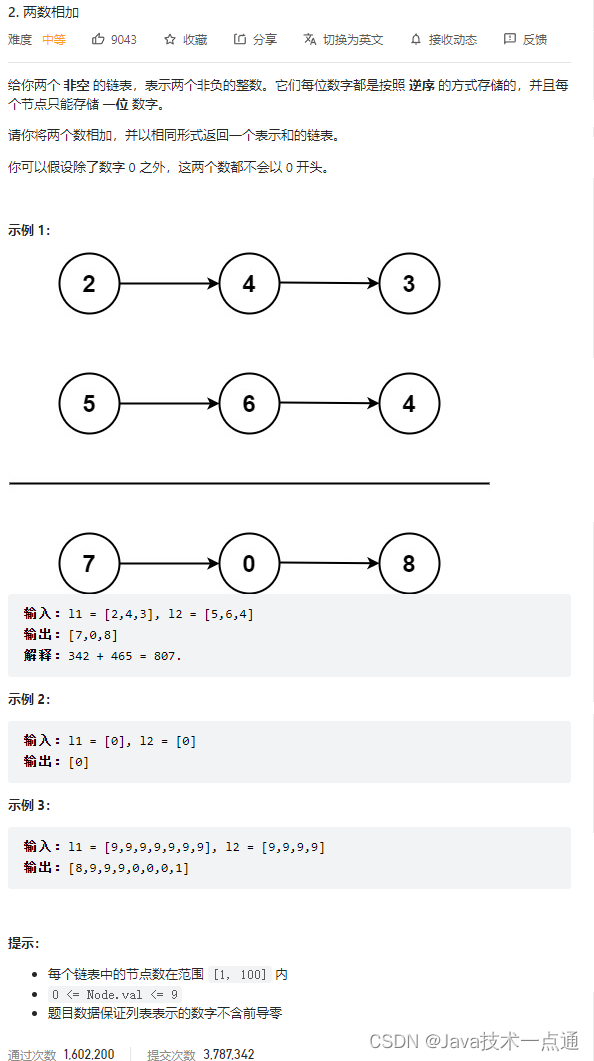
2. 思路分析

（模拟人工加法） O(n)
这是一道模拟题，直接模拟列竖式做加法的过程：

1. 从最低位至最高位，逐位相加，如果大于和等于10，则保留个位数字，同时向前一位加1；
2. 如果最高位有进位，则需在最前面补1。

列表的题目，有个常见的技巧：
添加一个虚拟头结点：ListNode *head = new ListNode(-1);，这样可以简化边界情况的判断。

时间复杂度：由于总共共扫描一遍，所以时间复杂度是O(n)。

---

3. 代码实现

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        auto dummy = new ListNode(-1), cur = dummy;
        int t = 0;
        while (l1 || l2 || t) {
            if (l1) t += l1->val, l1 = l1->next;
            if (l2) t += l2->val, l2 = l2->next;
            cur = cur->next = new ListNode(t % 10);
            t /= 10;
        }
        return dummy->next;
    }
};

---

三、无重复字符的最长子串

1. 题目描述

---

2. 思路分析

定义两个指针 $i,j(i<=j)$, 表示当前扫描到的子串是 $[i,j]$（闭区间）。扫描过程中维护一个哈希表unorderes_map<char, int> hash， 表示 $[i,j]$ 中每个字符出现的个数。

线性扫描，每次循环的流程如下：

1. 指针 $j$ 向后移一位，同时将哈希表中 $s[j]$ 的计数加一：hash[s[j]] ++;
2. 假设 $j$ 移动前的区间 $[i,j]$ 中没有重复字符，则 $j$ 移动后，只有 $s[j]$ 可能出现2次。因此我们不断向后移动 $i$，直至区间 $[i,j]$ 中 $s[j]$ 的个数等于1为止。

---

3. 代码实现

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        unordered_map<char, int> heap;
        int res = 0;
        for (int i = 0, j = 0; i < s.size(); i ++) {            
            heap[s[i]] ++;
            while (heap[s[i]] > 1) heap[s[j ++]] --;
            res = max(res, i - j + 1);
        }
        return res;
    }
};

---

四、寻找两个正序数组的中位数

1. 题目描述

---

2. 思路分析

3. 代码实现

---

五、最长回文子串

1. 题目描述

---

2. 思路分析

暴力枚举 O($2^2$)
首先枚举回文串的中心 $i$，然后分两种情况向两边扩展，直到遇到不同字符为止：

• 回文串长度是奇数，则依次判断 $s[i-k]==s[i+k],k=1,2,\mathrm{3.....}$
• 回文串长度是偶数，则依次判断 $s[i+k]==s[i+k-1],k=1,2,\mathrm{3....}$

如果遇到不同字符，则我们找到了以 $i$ 为中心的回文字符串边界。

---

3. 代码实现

class Solution {
public:
    string longestPalindrome(string s) {
        string res;
        for (int i = 0; i < s.size(); i ++ ) {
            int l = i - 1, r = i + 1;
            while (l >= 0 && r < s.size() && s[l] == s[r]) l --, r ++;
            if (res.size() < r - l - 1) res = s.substr(l + 1, r - l - 1);

            l = i, r = i + 1;
            while (l >= 0 && r < s.size() && s[l] == s[r]) l --, r ++;
            if (res.size() < r - l - 1) res = s.substr(l + 1, r - l - 1);
        }
        return res;
    }
};

---

六、正则表达式匹配

1. 题目描述

---

2. 思路分析

3. 代码实现

---

七、盛最多水的容器

1. 题目描述

---

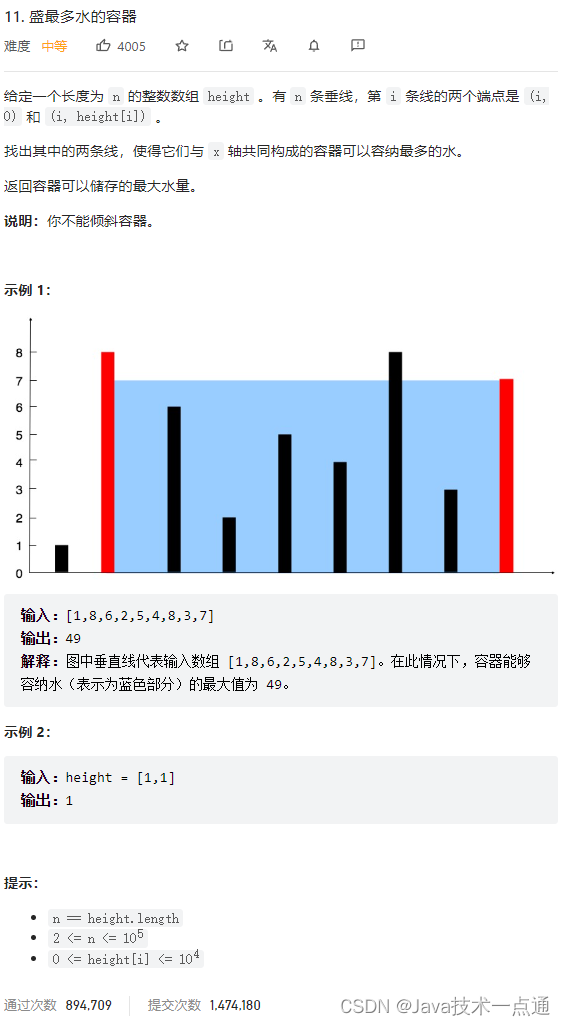
2. 思路分析

1. 初始化： 双指针 $i$，$j$分别指向水槽的左右两端；
2. 循环收窄： 直至双指针相遇时跳出；
   1. 更新面积最大值 $res$；
   2. 选定两板高度中的短板，向中间收窄一格；
3. 返回值： 返回面积最大值 $res$ 即可。

---

3. 代码实现

class Solution {
public:
    int maxArea(vector<int>& height) {
       int res = 0;
       for (int i = 0, j = height.size() - 1; i < j;) {
           res = max(res, min(height[i], height[j]) * (j - i));
           if (height[i] > height[j]) j --;
           else i ++; 
       } 
       return res;

    }
};

---

八、三数之和

1. 题目描述

---

2. 思路分析

双指针算法 $O(n^2)$

1. 枚举每个数，先确定 $nums[i]$，在排序后的情况下，通过双指针 $j$，$k$ 分别从左边 $j=i+1$ 和右边 $k=n-1$ 往中间靠拢，找到 $nums[i]+nums[j]+nums[k]==0$ 的所有符合条件的搭配；
2. 判重处理： 当 i > 0(i不是第一个数) && nums[i] == nums[i - 1]，表示当前确定好的数与上一个一样，需要直接 $ontinue$，同理，j && nums[j] == nums[j-1] 需要直接 $continue$;
3. while(j < k - 1 && nums[i] + nums[j] + nums[k - 1] >= 0) k -- //要找到满足最小的 $k$
   为什么 $j<k-1$
   试探法，如果 $k$ 的下一个数($k$的左边的数)满足就用下一个数。

---

3. 代码实现

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> res;
        sort(nums.begin(), nums.end());
        for (int i = 0; i < nums.size(); i ++ ) {
            if (i && nums[i] == nums[i - 1]) continue;
            for (int j = i + 1, k = nums.size() - 1; j < k; j ++ ) {
                if (j > i + 1 && nums[j] == nums[j - 1]) continue;
                while (j < k - 1 && nums[i] + nums[j] + nums[k - 1] >= 0) k --;
                if (nums[i] + nums[j] + nums[k] == 0) {
                    res.push_back({nums[i], nums[j], nums[k]});
                }
            }
        }
        return res;
    }
};

---

九、电话号码的字母组合

1. 题目描述

---

2. 思路分析

• 这是个排列组合问题，这个排列组合可以用树的形式表示出来；
• 当给定了输入字符串，比如：“23”，那么整棵树就构建完成了，如下：
  
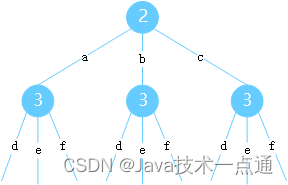
• 问题转化成了从根节点到空节点一共有多少条路径。

---

3. 代码实现

class Solution {
public:
    vector<string> ans;
    string strs[10] = {
        "", "", "abc", "def",
        "ghi", "jkl", "mno",
        "pqrs", "tuv", "wxyz",
    };

    vector<string> letterCombinations(string digits) {
        if (digits.empty()) return ans;
        dfs(digits, 0, "");
        return ans;
    }

    void dfs(string& digits, int u, string path) {
        if (u == digits.size()) ans.push_back(path);
        else {
            for (auto c : strs[digits[u] - '0']) 
                dfs(digits, u + 1, path + c);
        }
    }
};

---

十、删除链表的倒数第 N 个结点

1. 题目描述

---

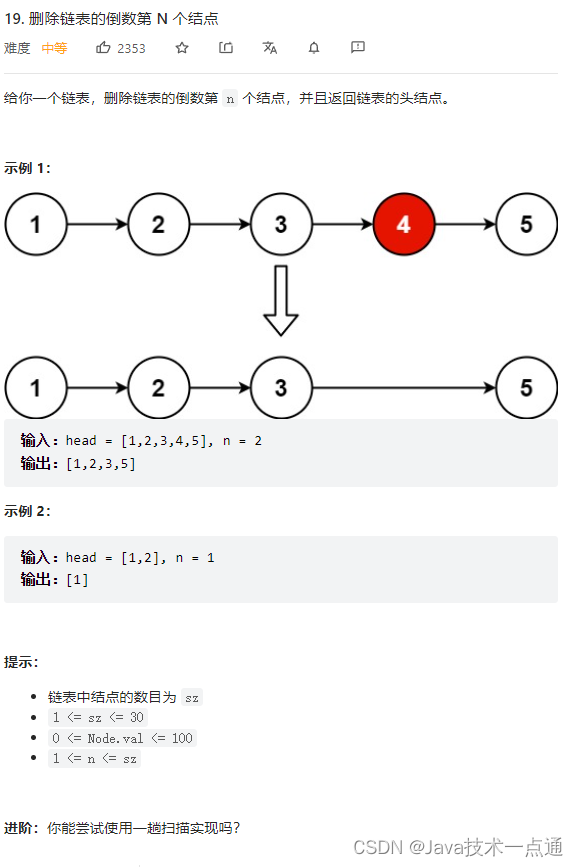
2. 思路分析

(两次遍历） $O(L)$

1. 第一次遍历求出链表的长度。
2. 第二次遍历删掉指定结点。

---

3. 代码实现

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        auto dummy = new ListNode(-1);
        dummy->next = head;

        int len = 0;
        for (auto p = dummy; p; p = p->next) len ++;

        auto p = dummy;
        for (int i = 0; i < len - n - 1; i ++) p = p->next;
        p->next = p->next->next;

        return dummy->next;
    }
};

---

 
非常感谢您阅读到这里，如果这篇文章对您有帮助，希望能留下您的点赞👍 关注💖 分享👥 留言💬thanks！！！