在前文中我们基于经典的YOLOv5开发构建了钢铁产业产品智能自动化检测识别系统,这里本文的主要目的是想要实践应用DETR这一端到端的检测模型来开发构建钢铁产业产品智能自动化检测识别系统。
DETR (DEtection TRansformer) 是一种基于Transformer架构的端到端目标检测模型。与传统的基于区域提议的目标检测方法(如Faster R-CNN)不同,DETR采用了全新的思路,将目标检测问题转化为一个序列到序列的问题,通过Transformer模型实现目标检测和目标分类的联合训练。
DETR的工作流程如下:
输入图像通过卷积神经网络(CNN)提取特征图。
特征图作为编码器输入,经过一系列的编码器层得到图像特征的表示。
目标检测问题被建模为一个序列到序列的转换任务,其中编码器的输出作为解码器的输入。
解码器使用自注意力机制(self-attention)对编码器的输出进行处理,以获取目标的位置和类别信息。
最终,DETR通过一个线性层和softmax函数对解码器的输出进行分类,并通过一个线性层预测目标框的坐标。
DETR的优点包括:
端到端训练:DETR模型能够直接从原始图像到目标检测结果进行端到端训练,避免了传统目标检测方法中复杂的区域提议生成和特征对齐的过程,简化了模型的设计和训练流程。
不受固定数量的目标限制:DETR可以处理变长的输入序列,因此不受固定数量目标的限制。这使得DETR能够同时检测图像中的多个目标,并且不需要设置预先确定的目标数量。
全局上下文信息:DETR通过Transformer的自注意力机制,能够捕捉到图像中不同位置的目标之间的关系,提供了更大范围的上下文信息。这有助于提高目标检测的准确性和鲁棒性。
然而,DETR也存在一些缺点:
计算复杂度高:由于DETR采用了Transformer模型,它在处理大尺寸图像时需要大量的计算资源,导致其训练和推理速度相对较慢。
对小目标的检测性能较差:DETR模型在处理小目标时容易出现性能下降的情况。这是因为Transformer模型在处理小尺寸目标时可能会丢失细节信息,导致难以准确地定位和分类小目标。
首先看下实例效果:
简单看下数据集:

PyTorch训练代码和DETR(DEDetection-TRansformer)的预训练模型。我们用Transformer替换了完全复杂的手工制作的对象检测管道,并将Faster R-CNN与ResNet-50匹配,使用一半的计算能力(FLOP)和相同数量的参数在COCO上获得42个AP。
官方项目地址在这里,如下所示:

可以看到目前已经收获了超过1.2w的star量,还是很不错的了。
DETR整体数据流程示意图如下所示:

官方也提供了对应的预训练模型,可以自行使用:
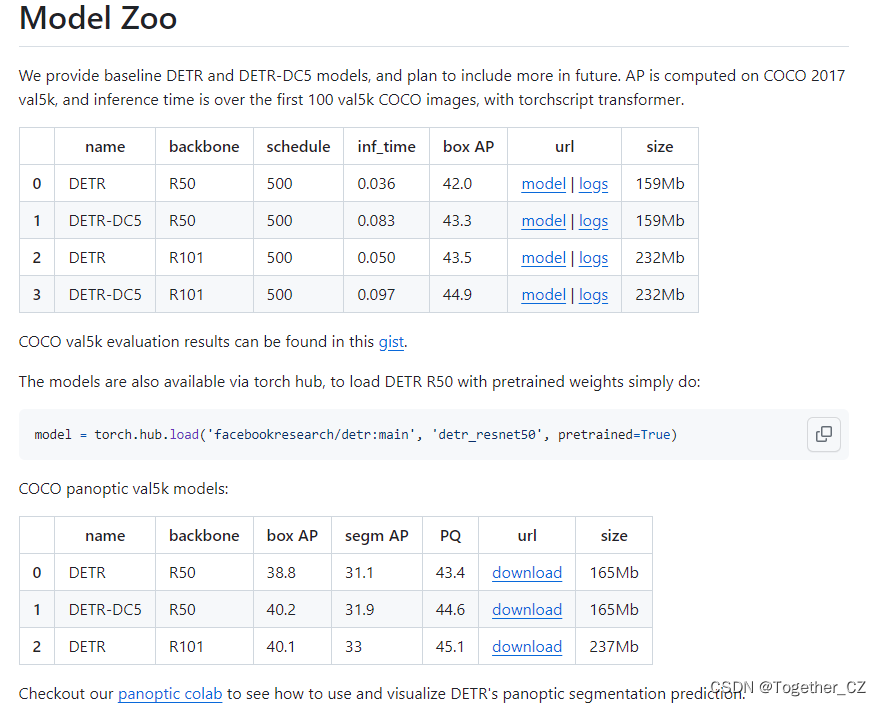
本文选择的预训练官方权重是detr-r50-e632da11.pth,首先需要基于官方的预训练权重开发能够用于自己的 个性化数据集的权重,如下所示:
pretrained_weights = torch.load("./weights/detr-r50-e632da11.pth")
num_class = 10 + 1
pretrained_weights["model"]["class_embed.weight"].resize_(num_class+1,256)
pretrained_weights["model"]["class_embed.bias"].resize_(num_class+1)
torch.save(pretrained_weights,'./weights/detr_r50_%d.pth'%num_class)因为这里我的类别数量为10,所以num_class修改为:10+1,根据自己的实际情况修改即可。生成后如下所示:
![]()
之后按照官方说明准备好数据集即可,启动训练模型命令如下所示:
python main.py --dataset_file "coco" --coco_path "/0000" --epoch 100 --lr=1e-4 --batch_size=32 --num_workers=0 --output_dir="outputs" --resume="weights/detr_r50_11.pth"
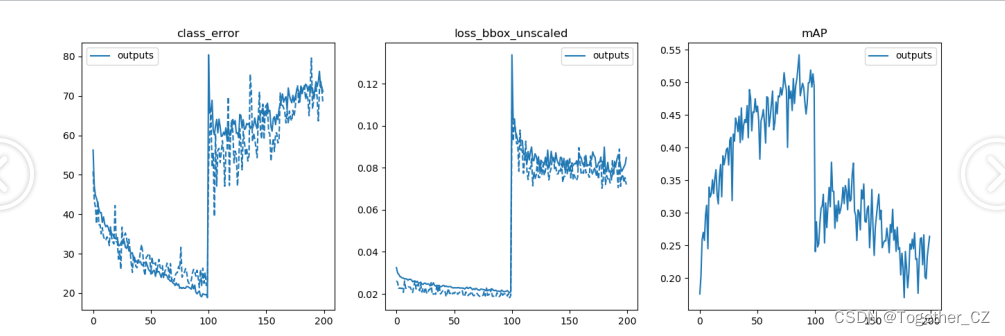
借助于plot_util.py模块可以实现对模型的评估和可视化,如下:
def plot_logs(logs, fields=('class_error', 'loss_bbox_unscaled', 'mAP'), ewm_col=0, log_name='log.txt'):
'''
Function to plot specific fields from training log(s). Plots both training and test results.
:: Inputs - logs = list containing Path objects, each pointing to individual dir with a log file
- fields = which results to plot from each log file - plots both training and test for each field.
- ewm_col = optional, which column to use as the exponential weighted smoothing of the plots
- log_name = optional, name of log file if different than default 'log.txt'.
:: Outputs - matplotlib plots of results in fields, color coded for each log file.
- solid lines are training results, dashed lines are test results.
'''
func_name = "plot_utils.py::plot_logs"
# verify logs is a list of Paths (list[Paths]) or single Pathlib object Path,
# convert single Path to list to avoid 'not iterable' error
if not isinstance(logs, list):
if isinstance(logs, PurePath):
logs = [logs]
print(f"{func_name} info: logs param expects a list argument, converted to list[Path].")
else:
raise ValueError(f"{func_name} - invalid argument for logs parameter.\n \
Expect list[Path] or single Path obj, received {type(logs)}")
# Quality checks - verify valid dir(s), that every item in list is Path object, and that log_name exists in each dir
for i, dir in enumerate(logs):
if not isinstance(dir, PurePath):
raise ValueError(f"{func_name} - non-Path object in logs argument of {type(dir)}: \n{dir}")
if not dir.exists():
raise ValueError(f"{func_name} - invalid directory in logs argument:\n{dir}")
# verify log_name exists
fn = Path(dir / log_name)
if not fn.exists():
print(f"-> missing {log_name}. Have you gotten to Epoch 1 in training?")
print(f"--> full path of missing log file: {fn}")
return
# load log file(s) and plot
dfs = [pd.read_json(Path(p) / log_name, lines=True) for p in logs]
fig, axs = plt.subplots(ncols=len(fields), figsize=(16, 5))
for df, color in zip(dfs, sns.color_palette(n_colors=len(logs))):
for j, field in enumerate(fields):
if field == 'mAP':
coco_eval = pd.DataFrame(
np.stack(df.test_coco_eval_bbox.dropna().values)[:, 1]
).ewm(com=ewm_col).mean()
axs[j].plot(coco_eval, c=color)
else:
df.interpolate().ewm(com=ewm_col).mean().plot(
y=[f'train_{field}', f'test_{field}'],
ax=axs[j],
color=[color] * 2,
style=['-', '--']
)
for ax, field in zip(axs, fields):
ax.legend([Path(p).name for p in logs])
ax.set_title(field)
def plot_precision_recall(files, naming_scheme='iter'):
if naming_scheme == 'exp_id':
# name becomes exp_id
names = [f.parts[-3] for f in files]
elif naming_scheme == 'iter':
names = [f.stem for f in files]
else:
raise ValueError(f'not supported {naming_scheme}')
fig, axs = plt.subplots(ncols=2, figsize=(16, 5))
for f, color, name in zip(files, sns.color_palette("Blues", n_colors=len(files)), names):
data = torch.load(f)
# precision is n_iou, n_points, n_cat, n_area, max_det
precision = data['precision']
recall = data['params'].recThrs
scores = data['scores']
# take precision for all classes, all areas and 100 detections
precision = precision[0, :, :, 0, -1].mean(1)
scores = scores[0, :, :, 0, -1].mean(1)
prec = precision.mean()
rec = data['recall'][0, :, 0, -1].mean()
print(f'{naming_scheme} {name}: mAP@50={prec * 100: 05.1f}, ' +
f'score={scores.mean():0.3f}, ' +
f'f1={2 * prec * rec / (prec + rec + 1e-8):0.3f}'
)
axs[0].plot(recall, precision, c=color)
axs[1].plot(recall, scores, c=color)
axs[0].set_title('Precision / Recall')
axs[0].legend(names)
axs[1].set_title('Scores / Recall')
axs[1].legend(names)
return fig, axs
结果如下所示:
iter 000: mAP@50= 24.0, score=0.317, f1=0.341
iter 050: mAP@50= 27.7, score=0.339, f1=0.400
iter latest: mAP@50= 26.4, score=0.348, f1=0.393
iter 000: mAP@50= 24.0, score=0.317, f1=0.341
iter 050: mAP@50= 27.7, score=0.339, f1=0.400
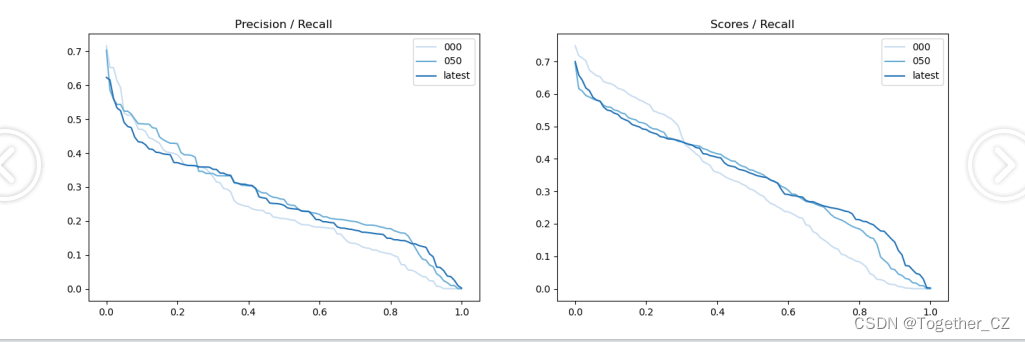
iter latest: mAP@50= 26.4, score=0.348, f1=0.393可视化如下所示:
【Precision曲线】
精确率曲线(Precision-Recall Curve)是一种用于评估二分类模型在不同阈值下的精确率性能的可视化工具。它通过绘制不同阈值下的精确率和召回率之间的关系图来帮助我们了解模型在不同阈值下的表现。
精确率(Precision)是指被正确预测为正例的样本数占所有预测为正例的样本数的比例。召回率(Recall)是指被正确预测为正例的样本数占所有实际为正例的样本数的比例。
绘制精确率曲线的步骤如下:
使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
对于每个阈值,计算相应的精确率和召回率。
将每个阈值下的精确率和召回率绘制在同一个图表上,形成精确率曲线。
根据精确率曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
通过观察精确率曲线,我们可以根据需求确定最佳的阈值,以平衡精确率和召回率。较高的精确率意味着较少的误报,而较高的召回率则表示较少的漏报。根据具体的业务需求和成本权衡,可以在曲线上选择合适的操作点或阈值。
精确率曲线通常与召回率曲线(Recall Curve)一起使用,以提供更全面的分类器性能分析,并帮助评估和比较不同模型的性能。
【Recall曲线】
召回率曲线(Recall Curve)是一种用于评估二分类模型在不同阈值下的召回率性能的可视化工具。它通过绘制不同阈值下的召回率和对应的精确率之间的关系图来帮助我们了解模型在不同阈值下的表现。
召回率(Recall)是指被正确预测为正例的样本数占所有实际为正例的样本数的比例。召回率也被称为灵敏度(Sensitivity)或真正例率(True Positive Rate)。
绘制召回率曲线的步骤如下:
使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
对于每个阈值,计算相应的召回率和对应的精确率。
将每个阈值下的召回率和精确率绘制在同一个图表上,形成召回率曲线。
根据召回率曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
通过观察召回率曲线,我们可以根据需求确定最佳的阈值,以平衡召回率和精确率。较高的召回率表示较少的漏报,而较高的精确率意味着较少的误报。根据具体的业务需求和成本权衡,可以在曲线上选择合适的操作点或阈值。
召回率曲线通常与精确率曲线(Precision Curve)一起使用,以提供更全面的分类器性能分析,并帮助评估和比较不同模型的性能。
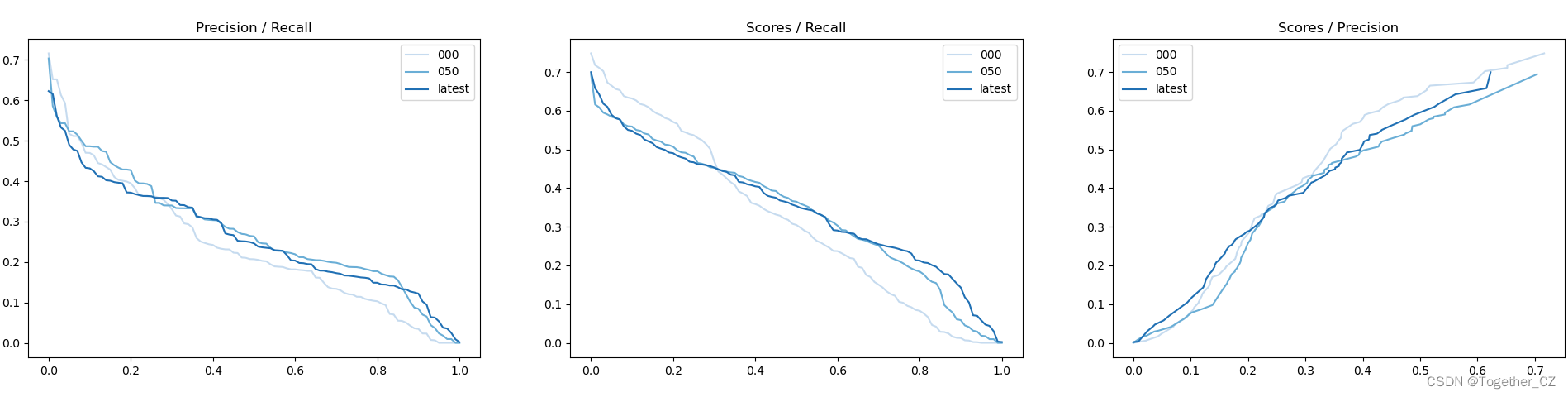
【PR曲线】
精确率-召回率曲线(Precision-Recall Curve)是一种用于评估二分类模型性能的可视化工具。它通过绘制不同阈值下的精确率(Precision)和召回率(Recall)之间的关系图来帮助我们了解模型在不同阈值下的表现。
精确率是指被正确预测为正例的样本数占所有预测为正例的样本数的比例。召回率是指被正确预测为正例的样本数占所有实际为正例的样本数的比例。
绘制精确率-召回率曲线的步骤如下:
使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
对于每个阈值,计算相应的精确率和召回率。
将每个阈值下的精确率和召回率绘制在同一个图表上,形成精确率-召回率曲线。
根据曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
精确率-召回率曲线提供了更全面的模型性能分析,特别适用于处理不平衡数据集和关注正例预测的场景。曲线下面积(Area Under the Curve, AUC)可以作为评估模型性能的指标,AUC值越高表示模型的性能越好。
通过观察精确率-召回率曲线,我们可以根据需求选择合适的阈值来权衡精确率和召回率之间的平衡点。根据具体的业务需求和成本权衡,可以在曲线上选择合适的操作点或阈值。
感兴趣的话可以自行动手实践尝试下!