拓扑排序

AOV-网

无环的有向图称作有向无环图。
这种用顶点表示活动，用弧表示活动间的优先关系的有向图称为以顶点为活动的网（Activity On Vertex Network）,简称AOV-网。
在网中，若从顶点vi到vj有一条有向路径，则vi是vj的前驱，vj是vi的后继。若<vi,vj>是网中的一条弧，则vi是vj的直接前驱，vj是vi的直接后继。
在AOV-网中，不应该出现环。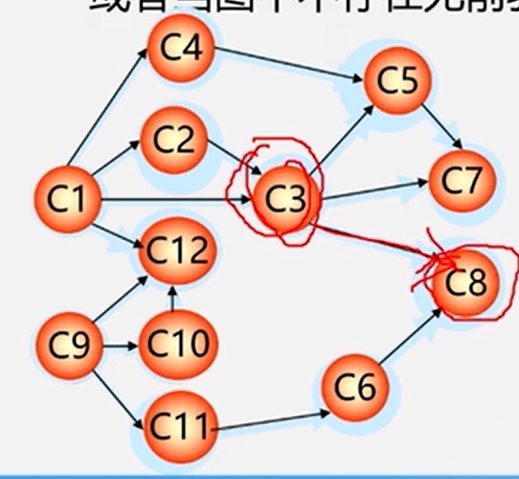
例如，这里的c1是c5的前驱，c5是c1的后继。
c1是c2的直接前驱，c2是c1的直接后继。

拓扑排序的方法

• 在有向图中选一个没有前驱的顶点且输出之。
• 从图中删除该顶点和没有以他为尾的弧。
• 重复上述步骤，直至全部顶点均已输出；或者当图中不存在无前驱结点的顶点为止。
  
  一个AOV网的拓扑排序不是唯一的。
  比如，将c1去掉后，后面可以选择的顶点有c2，c4，c9。

拓扑排序的一个重要应用：

检测AOV网中是否存在环的方法：
对有向图构造其顶点的拓扑有序序列，若网上所有的顶点都在拓扑有序序列中，则该AOV图必定不存在环。

拓扑排序的算法

算法步骤：
①求出各顶点的入度并存在数组indegree[i]中，使入度为0的顶点入栈。
②只要栈不空，则重复以下操作：

• 使栈顶顶点vi出栈，并保存在拓扑序列数组topo中；
• 对顶点vi的每个邻接点vk的入度减1，如果vk的入度变为0，则使vk入栈。
  ③如果出现顶点个数少于AOV-网的顶点个数，则网中存在有向环，无法进行拓扑排序，否则拓扑排序成功。